콤팩트 리 군
|
Read other articles:

2019 song by Inna Sin TiSingle by Innafrom the album Yo LanguageSpanishReleased18 January 2019Length2:49LabelGlobalRoc NationSongwriter(s)Elena Alexandra ApostoleanuCristina Maria ChiluizaProducer(s)David CienteInna singles chronology Iguana (2018) Sin Ti (2019) Tu Manera (2019) Sin Ti (English: Without You) is a song by Romanian singer Inna, digitally released on 18 January 2019 by Global Records and Roc Nation as the third single from her sixth studio album Yo (2019). It was written by Inna...
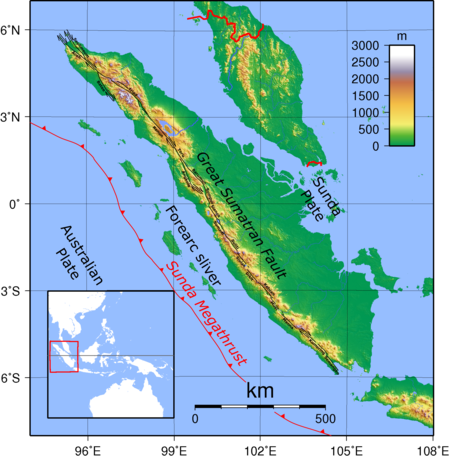
Gempa bumi Sumatra Barat 2009PadangPekanbaruMedanPalembangWaktu UTC2009-09-30 10:16:10ISC13801688USGS-ANSSComCatTanggal setempat30 September 2009 (2009-09-30)Waktu setempat17:16:10 WIBKekuatan7.6 MwKedalaman90 km (56 mi)Episentrum0°43′N 99°58′E / 0.71°N 99.97°E / 0.71; 99.97Koordinat: 0°43′N 99°58′E / 0.71°N 99.97°E / 0.71; 99.97JenisReverseWilayah bencanaIndonesiaIntensitas maks.VIII (Parah)Tsunami2...

Keuskupan Fano-Fossombrone-Cagli-PergolaDioecesis Fanensis-Forosemproniensis-Calliensis-PergulanaKatolik Katedral FanoLokasiNegara ItaliaProvinsi gerejawiPesaroStatistikLuas1.100 km2 (420 sq mi)Populasi- Total- Katolik(per 2006)128.916126,064 (97.8%)Paroki74InformasiDenominasiGereja KatolikRitusRitus RomaPendirianAbad ke-1KatedralBasilica Cattedrale di S. Maria Maggiore (Fano)KonkatedralConcattedrale di Ss. Aldebrando e Agostino (Fossombrone)Concattedra...

Bodhisattva duduk bermeditasi menuju samadhi, Afganistan 2 Masehi. Samadhi (bahasa Sansekerta: समाधि) adalah sebuah ritual konsentrasi tingkat tinggi, melampaui kesadaran alam jasmani yang terdapat dalam agama Hindu, Buddhisme, Jainisme, Sikhisme, dan aliran yoga.[1][2] Samadhi juga merupakan fase tertinggi dalam delapan fase penguasaan Yoga.[2] Ketika memasuki fase samadhi, kemampuan analitis dan logika menjadi tak berfungsi atau diam.[2] Menurut Kam...

This article's lead section may be too short to adequately summarize the key points. Please consider expanding the lead to provide an accessible overview of all important aspects of the article. (October 2015) 2015 studio album by Tamar BraxtonCalling All LoversDeluxe edition cover. Standard edition uses the same cover but in a slightly different color and is no longer available for retail.Studio album by Tamar BraxtonReleasedOctober 2, 2015Recorded2014–15StudioOasis Mastering (Burb...
Overview of and topical guide to the Collectivity of Saint Martin See also: Index of Saint Martin (France)-related articles The location of Saint Martin An enlargeable map of the French Overseas Collectivity of Saint Martin A map of the island of Saint Martin The following outline is provided as an overview of and topical guide to the Collectivity of Saint Martin: The Collectivity of Saint Martin (French: Collectivité de Saint-Martin) is an overseas collectivity of France located in the Leew...

Mountain in San Diego County, California, United States PalomarMonte Palomar (Spanish)View of the Palomar Observatory located near the High Point summit of the Palomar Mountain range.Highest pointElevation6,142 ft (1,872 m) NAVD 88[1]Prominence2,856 ft (871 m)[2]ListingSan Diego peak list[3]Coordinates33°21′49″N 116°50′11″W / 33.363483514°N 116.836394236°W / 33.363483514; -116.836394236[1&#...

Chemical compound ADB-FUBIATALegal statusLegal status BR: Class F2 (Prohibited psychotropics)[1] Identifiers IUPAC name (2S)-2-[[2-[1-[(4-fluorophenyl)methyl]indol-3-yl]acetyl]amino]-3,3-dimethylbutanamide PubChem CID165361558ChemSpider114876989Chemical and physical dataFormulaC23H26FN3O2Molar mass395.478 g·mol−13D model (JSmol)Interactive image SMILES CC(C)(C)[C@@H](C(=O)N)NC(=O)CC1=CN(C2=CC=CC=C21)CC3=CC=C(C=C3)F InChI InChI=1S/C23H26FN3O2/c1-23(2,3)21(22(25)29)26-20(28...

Questa voce o sezione sull'argomento centri abitati della Toscana non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Radicofanicomune Radicofani – Veduta LocalizzazioneStato Italia Regione Toscana Provincia Siena AmministrazioneSindacoFrancesco Fabbrizzi (centro-sinistra, lista civica - Oltre per Radicofani e Contignano) dal 26-5-...

ХристианствоБиблия Ветхий Завет Новый Завет Евангелие Десять заповедей Нагорная проповедь Апокрифы Бог, Троица Бог Отец Иисус Христос Святой Дух История христианства Апостолы Хронология христианства Раннее христианство Гностическое христианство Вселенские соборы Н...

Voce principale: Fiamma Monza 1970. A.S. Fiammamonza DilettanteStagione 2009-2010Sport calcio SquadraFiamma Monza 1970 Allenatore Aristide Poma (1ª-3ª) Liliana Luisa Paggi (4ª-22ª) Presidente Roberto Lo Grasso Serie A12º posto, retrocessa in Serie A2 Coppa ItaliaQuarta fase Maggiori presenzeCampionato: Balconi (22) Miglior marcatoreCampionato: Ricco (8) StadioStadio Gino Alfonso Sada 2008-2009 2010-2011 Si invita a seguire il modello di voce Questa voce raccoglie le informazioni riguard...

Міністерство оборони України (Міноборони) Емблема Міністерства оборони та Прапор Міністерства оборони Будівля Міністерства оборони у КиєвіЗагальна інформаціяКраїна УкраїнаДата створення 24 серпня 1991Попередні відомства Міністерство оборони СРСР Народний комісарі...

Australian RL coach and former Australia international rugby league footballer Les MeadPersonal informationFull nameLeslie Edward Huon MeadBorn(1909-06-09)9 June 1909Mosman, New South WalesDied21 October 1996(1996-10-21) (aged 87)Killarney Vale, New South WalesPlaying informationPositionHalfback Club Years Team Pld T G FG P 1930 Western Suburbs 5 3 3 0 15 1931 Wauchope 1932–37 Western Suburbs 70 27 169 0 419 1938–40 Wauchope 1941 Western Suburbs 2 0 0 0 0 Total 77 30 172 0 434 R...

Berikut adalah calon anggota Dewan Perwakilan Daerah provinsi Jawa Tengah untuk periode 2024-2029, ditampilkan berdasarkan nomor urut masing-masing calon. Nomor Urut Potret Nama Jenis Kelamin Domisili 1 Dr. H. Abdul Kholik, S.H., M.Si. Laki-laki Cilacap, Jawa Tengah 2 Agus Mujayanto Laki-laki Demak, Jawa Tengah 3 Ahmad Baligh Mu'aidi, S.Pd.I. Laki-laki Rembang, Jawa Tengah 4 Ir. H. Bambang Sutrisno, M.M. Laki-laki Kota Surakarta, Jawa Tengah 5 Casytha Arriwi Kathmandu, S.E. Perempuan Bantul, ...

روجيليو فونيس موري معلومات شخصية الاسم الكامل روجيليو غابرييل فونيس موري الميلاد 5 مارس 1991 (العمر 33 سنة)ميندوزا، الأرجنتين الطول 1.85 م (6 قدم 1 بوصة) مركز اللعب مهاجم الجنسية الأرجنتين المكسيك أخوة وأخوات راميرو فونيس موري معلومات النادي النادي الحالي مونتيري ...

Polish journalist (born 1964) This biography of a living person relies too much on references to primary sources. Please help by adding secondary or tertiary sources. Contentious material about living persons that is unsourced or poorly sourced must be removed immediately, especially if potentially libelous or harmful.Find sources: Wojciech Cejrowski – news · newspapers · books · scholar · JSTOR (January 2009) (Learn how and when to remove this message...

Annual fan convention in Alberta, Canada Calgary Comic and Entertainment ExpoStatusActiveGenreComic, pop cultureVenueStampede ParkLocation(s)Calgary, AlbertaCountryCanadaInaugurated2005Attendance95,000 in 2017[1]Organized byFan Expo HQ/Informa ConnectWebsitewww.calgaryexpo.com Calgary Expo, known in full as the Calgary Comic and Entertainment Expo, is an annual fan convention held at Stampede Park in Calgary, Alberta, Canada. Originally taking place in the BMO Centre, the show began i...

2012 American film Abducted: The Carlina White StoryWritten byElizabeth HunterDirected byVondie Curtis-HallStarringAunjanue EllisKeke PalmerSherri ShepherdRoger CrossTheme music composerTerence BlanchardCountry of originUnited StatesCanadaOriginal languageEnglishProductionProducersMary MartinCraig PiligianAlan GasnerRunning time90 minutesProduction companyPilgrim Studios[1]Original releaseNetworkLifetimeReleaseOctober 6, 2012 (2012-10-06) Abducted: The Carlina White Sto...

British pre-grouping railway company (1859–1899/1922) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: London, Chatham and Dover Railway – news · newspapers · books · scholar · JSTOR (June 2013) (Learn how and when to remove this message) Badge of the LCDR from the first Blackfriars Railway Bridge The Londo...
هذه المقالة بحاجة لصندوق معلومات. فضلًا ساعد في تحسين هذه المقالة بإضافة صندوق معلومات مخصص إليها. دراسات الثقافة الشعبية هي دراسة الثقافة الشعبية من منظورها النقدي والتي تجمع بين دراسات الاتصال والدراسات الثقافية. أول مؤسسة تقدم درجة البكالوريوس والماجستير في الثقافة ا�...
























![{\displaystyle \mathbb {R} [{\mathfrak {t}}]=\mathbb {R} \oplus {\mathfrak {t}}^{*}\oplus \operatorname {Sym} ^{2}{\mathfrak {t}}^{*}\oplus \dotsb }](https://wikimedia.org/api/rest_v1/media/math/render/svg/72509ca96539c2ec5e11c050469bd1b8458e8c5c)
![{\displaystyle \mathbb {R} [{\mathfrak {t}}]^{\operatorname {W} ({\mathfrak {g}})}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/305931d87d006386fe2ee0d701b84feebec54250)


![{\displaystyle \left({\frac {\mathbb {R} [{\mathfrak {t}}]}{\mathbb {R} [{\mathfrak {t}}]^{\operatorname {Weyl} ({\mathfrak {g}})}}}\right)_{(2)}\cong \operatorname {H} (G/T;\mathbb {R} )}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d9c44a152b43f3aad52b0d6d2beee790498ee886)





















