제주청사관리소

제주청사관리소
설립일 2006년 12월 12일
소재지 제주특별자치도 제주시 청사로 59
상급기관 정부청사관리본부

제주청사관리소(濟州廳舍管理所)는 정부제주지방합동청사보수·유지·관리에 관한 관리본부의 사무를 분장하는 정부청사관리본부의 소속기관이다.[1] 2006년 12월 12일 발족하였으며, 제주특별자치도 제주시 청사로 59에 위치하고 있다. 소장은 서기관 또는 기술서기관으로 보하되,[2] 임기제공무원으로 보할 수 있다.

연혁

  • 2006년 12월 12일: 정부청사관리소 소속으로 제주청사관리소 설치.
  • 2016년 12월 27일: 정부청사관리본부 소속으로 변경.

같이 보기

각주

  1. ↑ 대한민국 행정자치부 (2016년 12월 27일). “행정자치부와 그 소속기관 직제”. 《국가법령정보센터》. 대한민국 법제처. 2017년 1월 29일에 확인함. 
  2. ↑ 대한민국 행정자치부 (2016년 12월 27일). “행정자치부와 그 소속기관 직제 시행규칙”. 《국가법령정보센터》. 대한민국 법제처. 2017년 1월 29일에 확인함. 
이 글은 제주특별자치도에 관한 토막글입니다. 여러분의 지식으로 알차게 문서를 완성해 갑시다.
이 글은 대한민국의 행정기관에 관한 토막글입니다. 여러분의 지식으로 알차게 문서를 완성해 갑시다.

Read other articles:

Ju Ji-hoon

Ini adalah nama Korea; marganya adalah Joo. Ju Ji-hoonJu Ji-hoon pada Oktober 2018LahirJoo Young-hoon16 Mei 1982 (umur 41)Seoul, Korea SelatanNama lainJoo Ji-hoonAlmamaterUniversitas KyonggiTahun aktif2003–sekarangAgenH& Entertainment KeyEast Youbeak Entertainment Universal D (Jepang)Nama KoreaHangul주지훈 Hanja朱智勳 Alih AksaraJu Ji-hunMcCune–ReischauerChu Chihun Situs webJu Ji-hoon Ju Ji-hoon (Hangul: 주지훈; lahir 16 Mei 1982) adalah aktor Korea Se...

 

العلاقات الأمريكية الليختنشتانية

العلاقات الأمريكية الليختنشتانية الولايات المتحدة ليختنشتاين   الولايات المتحدة   ليختنشتاين تعديل مصدري - تعديل   العلاقات الأمريكية الليختنشتانية هي العلاقات الثنائية التي تجمع بين الولايات المتحدة وليختنشتاين.[1][2][3][4][5] مقارنة بين ا�...

 

العلاقات اليونانية السريلانكية

العلاقات اليونانية السريلانكية اليونان سريلانكا   اليونان   سريلانكا تعديل مصدري - تعديل   العلاقات اليونانية السريلانكية هي العلاقات الثنائية التي تجمع بين اليونان وسريلانكا.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية للدولتي�...

The Diamond Age

1995 novel by Neal Stephenson The Diamond Age First editionAuthorNeal StephensonCover artistBruce JensenCountryUnited StatesLanguageEnglishGenreScience fictionPostcyberpunkPublisherBantam Spectra (U.S.)Publication dateFebruary 1995Media typePrint (hardback & paperback) & Audio Book (Cassette, MP3 CD, Audio download. Narrator: Jennifer Wiltsie) & e-bookPages455 (hardcover), 512 (paperback)AwardsLocus Award for Best Science Fiction Novel (1996), Hugo Award for Best Novel (...

 

All-Russian Institute Of Aviation Materials

All-Russian Institute Of Aviation MaterialsNative nameВсероссийский научно-исследовательский институт авиационных материаловCompany typefederal state unitary enterpriseIndustryaerospaceFounded1932; 92 years ago (1932)HeadquartersMoscow, RussiaArea servedEurope and AsiaKey peopleEvgeny Kablov, Director GeneralProductsindustrial materialsOwnerRussian FederationNumber of employeesover 1700Websitewww.viam.ru/en The...

 

Jasło

Place in Subcarpathian Voivodeship, PolandJasłoStarosty in Jaslo, Gazebo in City Park, Palace, Parish Church, Church of Sts. Stanislaus, Promenade and historic buildings, Jewish Cemetery, Tadeusz Kosciuszko Monument FlagCoat of armsJasłoCoordinates: 49°44′52″N 21°28′17″E / 49.74778°N 21.47139°E / 49.74778; 21.47139Country PolandVoivodeship SubcarpathianCountyJasłoGminaJasło (urban gmina)Established12th centuryTown rights1365Government •...

Compagnie des chemins de fer des Ardennes

Compagnie des Ardennes Création 11 juillet 1855 Disparition 1er janvier 1864 Fondateur(s) Paul de Noailles (président), Jules François Riché Successeur Compagnie de l'Est Forme juridique société anonyme Siège social Paris France modifier  La Compagnie des chemins de fer des Ardennes, anciennement dénommée Compagnie du chemin de fer des Ardennes et de l'Oise, est une société anonyme qui constitua un réseau de voies ferrées sur le territoire français entre 1855 et 1863....

 

Army of the Tsardom of Russia

Army of Tsardom of RussiaВойско Русского государства (Russian)Founded15th centuryDisbanded1682HeadquartersMoscowLeadershipFormer MilitaryArmies of Rus'Related articlesHistoryMilitary history of Russia Muscovite–Lithuanian WarsRusso-Kazan Wars (1439-1552)Russian-Livonian War (1480-1481)Smolensk War (1632-1634) Army of the Tsardom of Russia (Russian: Армия Русского государства) known also as the Forces of the Russian State (Russian: Во�...

 

Paradies, wo bist du?

Paradies, wo bist du? Chanson de Ulla Wiesner Sortie 1965 Durée 2:32 Langue Allemand Genre Schlager Format 45t Auteur Hans BlumBarbara Kist Compositeur Hans BlumBarbara Kist Label Telefunken Chansons représentant l'Allemagne au Concours Eurovision de la chanson Man gewöhnt sich so schnell an das Schöne(1964) Die Zeiger der Uhr(1966)modifier Paradies, wo bist du? (en français, Paradis, où es-tu ?) est la chanson représentant l'Allemagne au Concours Eurovision de la chanson 19...

Milan Mojsilović

Milan Mojsilović (Sirilik Serbia: Милан Мојсиловић; lahir 3 Agustus 1967) adalah Kepala Staf Umum Angkatan Bersenjata Serbia, diangkat pada 14 September 2018.Milan MojsilovićJenderal Milan Mojsilović pada tahun 2018Lahir3 Agustus 1967 (umur 56)Mitrovica, YugoslaviaPengabdian Yugoslavia FR Yugoslavia Serbia dan Montenegro SerbiaDinas/cabang Tentara Rakyat Yugoslavia Angkatan Bersenjata Serbia dan Montenegro Angkatan Bersenjata SerbiaLama dinas199...

 

Oberpfalz

Lambang dari Oberpfalz Oberpfalz (bahasa Inggris: Upper Palatinate) adalah satu dari tujuh distrik administratif di Bavaria, Jerman, yang terletak di Bavaria Timur. Oberpfalz (Upper Palatinate) di Bavaria secara tradisional telah diperintah oleh Wangsa Wittelsbach oleh para elektor mereka di Palatinate sepanjang Sungai Rhein. Wangsa Wittelsbach tinggal dalam kemegahan istana di Heidelberg dan kemudian tinggal di istana Barok di Mannheim; yang merupakan istana terbesar di Jerman. Pada tahu...

 

中華民國國軍中的中共間諜列表

 本表是動態列表，或許永遠不會完結。歡迎您參考可靠來源來查漏補缺。 潛伏於中華民國國軍中的中共間諜列表收錄根據公開資料來源，曾潛伏於中華民國國軍、被中國共產黨聲稱或承認，或者遭中華民國政府調查審判，為中華人民共和國和中國人民解放軍進行間諜行為的人物。以下列表以現今可查知時間為準，正確的間諜活動或洩漏機密時間可能早於或晚於以下所歸�...

مورغان هيل

مورغان هيل    علم   الإحداثيات 37°07′50″N 121°39′16″W / 37.130555555556°N 121.65444444444°W / 37.130555555556; -121.65444444444   [1] تاريخ التأسيس 10 نوفمبر 1906  تقسيم إداري  البلد الولايات المتحدة[2][3]  التقسيم الأعلى مقاطعة سانتا كلارا  خصائص جغرافية  المساحة 33.05490...

 

Belgium in the Eurovision Song Contest 2019

Eurovision Song Contest 2019Country BelgiumNational selectionSelection processInternal selectionSelection date(s)Artist: 14 January 2019Song: 28 February 2019Selected entrantEliotSelected songWake UpSelected songwriter(s)Pierre DumoulinEliot VassamilletFinals performanceSemi-final resultFailed to qualify (13th)Belgium in the Eurovision Song Contest ◄2018 • 2019 • 2020► Belgium participated in the Eurovision Song Contest 2019 with the song Wake Up wr...

 

Touat

Localisation de la région du Touat en Algérie. Le Touat[1] est une région de l'ouest du Sahara algérien, située au sud-ouest du Grand Erg occidental, dans la wilaya d'Adrar. Touat signifie en langue berbère « localité habitée »[réf. nécessaire]. La composition de la population du Touat est diverse. On y retrouve des Subsahariens, des Berbères, des Haratines, des Arabes. La région a été peuplée par une communauté juive dans l'Antiquité et au Moyen Âg...

Poi (food)

Traditional staple food in the Polynesian diet Not to be confused with Poi (dessert). PoiA bowl of poi showing typical consistencyAlternative namesPopoiTypePuréePlace of originPolynesiaRegion or stateCook Islands, French Polynesia, HawaiiMain ingredientsStarchy vegetable  Media: Poi Poi is a traditional staple food in the Polynesian diet, made from taro. Traditional poi is produced by mashing cooked taro on a wooden pounding board (papa kuʻi ʻai), with a carved pestle (pōhaku ku�...

 

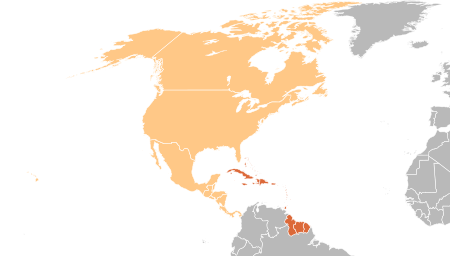
Caribbean Football Union

Governing body for association football in the Caribbean Caribbean Football UnionThe former CFU emblemAbbreviationCFUFormation28 January 1978; 46 years ago (1978-01-28)TypeSports organisationHeadquartersJamaicaMembership 31 member associationsSecretary GeneralCamara DavidPresidentRandy HarrisWebsitewww.caribbeanfootballunion.org The Caribbean Football Union (CFU) is the representative organization for football associations in the Caribbean. It represents 25 FIFA member natio...

 

Congo (chimpanzee)

Chimpanzee who learned how to draw and paint CongoA painting by CongoSpeciesChimpanzee (Pan troglodytes)SexMaleBornc. 1954Died1964 (aged 9–10)London Zoo, London, EnglandCause of deathTuberculosisYears active1956-1959Known forLearning to draw and paint Congo (1954–1964) was a chimpanzee artist and painter. Zoologist, author and surrealist painter Desmond Morris first observed his abilities when the chimpanzee was offered a pencil and paper at two years of age. By t...

Monticello Raceway

Horse racing track in New York (state), US Monticello RacewayMonticello Raceway in October 2008Location204 Route 17BMonticello, New YorkCoordinates41°40′07″N 74°42′52″W / 41.66872°N 74.714563°W / 41.66872; -74.714563Owned byEmpire ResortsDate openedJune 27, 1958Race typeharness racingOfficial website Monticello Raceway is a harness racing track and former casino in Monticello, New York. It is owned and operated by Empire Resorts. The racetrack is nicknamed ...

 

Logistic function

S-shaped curve For the recurrence relation, see Logistic map. A logistic function or logistic curve is a common S-shaped curve (sigmoid curve) with the equation f ( x ) = L 1 + e − k ( x − x 0 ) {\displaystyle f(x)={\frac {L}{1+e^{-k(x-x_{0})}}}} where L {\displaystyle L} is the carrying capacity, the supremum of the values of the function; k {\displaystyle k} is the logistic growth rate, the steepness of the curve; and x 0 {\displaystyle x_{0}} is the x {\displaystyle x} value ...