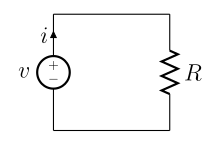
전기 회로
|
Read other articles:

Colobus merah Delta Niger Status konservasi Kritis (IUCN 3.1)[1] Klasifikasi ilmiah Kerajaan: Animalia Filum: Khordata Kelas: Mamalia Ordo: Primata Famili: Cercopithecidae Genus: Piliocolobus Spesies: P. epieni Nama binomial Piliocolobus epieni(Groves, 2007) Sinonim Procolobus badius epieni Procolobus pennantii epieni Colobus merah Delta Niger (Piliocolobus epieni) adalah sebuah spesies terancam kritis dari monyet colobus yang menjadi endemik di bagian barat Delta Niger. He...

Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber: Lontong kikil – berita · surat kabar · buku · cendekiawan · JSTOR Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel...

لمعانٍ أخرى، طالع دانفيل (توضيح). دانفيل الإحداثيات 37°38′45″N 84°46′21″W / 37.645833333333°N 84.7725°W / 37.645833333333; -84.7725 [1] تاريخ التأسيس 1785 تقسيم إداري البلد الولايات المتحدة[2][3] التقسيم الأعلى مقاطعة بويل عاصمة لـ مقاطعة بويل خصا...

Questa voce o sezione sugli argomenti imprenditori italiani e cantanti italiani non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Segui i suggerimenti dei progetti di riferimento 1, 2. Gianni Ravera in una foto-cartolina pubblicitaria degli anni quaranta Giandomenico Ravera, nato Lenin Ravera e meglio noto come Gianni Ravera (Chiaravalle, 9 aprile 1920 –...

IM-1IM-1 Odysseus kelas Nova-C dalam persiapan peluncuranJenis misiPendaratan BulanOperatorIntuitive MachinesCOSPAR ID2024-030ASATCAT no.58963Durasi misi51 hari, 12 jam dan 26 menit (sedang berlangsung)43 hari, 19 jam dan 8 menit (sejak mendarat) Properti wahanaWahana antariksaNova-CProdusenIntuitive MachinesMassa luncur1.900 kilogram (4.200 pon) Awal misiTanggal luncurTemplat:Start date text UTC (12:05 a.m. EST)Roket peluncurFalcon 9 Block 5 (B1060.18)...

Myoleja lucida Klasifikasi ilmiah Kerajaan: Animalia Filum: Arthropoda Kelas: Insecta Ordo: Diptera Famili: Tephritidae Spesies: Myoleja lucida Myoleja lucida adalah spesies lalat yang tergolong famili Tephritidae. Spesies ini juga merupakan bagian dari ordo Diptera, kelas Insecta, filum Arthropoda, dan kingdom Animalia. Kebanyakan anggota spesies ini bertelur dalam jaringan tumbuhan, tempat larva menemukan makanan pertamanya setelah lahir. Lalat dewasa biasanya berumur sangat pendek. Bebera...

この項目には、一部のコンピュータや閲覧ソフトで表示できない文字が含まれています(詳細)。 数字の大字(だいじ)は、漢数字の一種。通常用いる単純な字形の漢数字(小字)の代わりに同じ音の別の漢字を用いるものである。 概要 壱万円日本銀行券(「壱」が大字) 弐千円日本銀行券(「弐」が大字) 漢数字には「一」「二」「三」と続く小字と、「壱」「�...

Church cantata by Johann Sebastian Bach (c. 1708) Actus tragicus redirects here. For the Israeli comics group, see Actus Tragicus (comics). Gottes Zeit ist die allerbeste ZeitBWV 106Church cantata by J. S. BachOrgan of the church Divi Blasii, MühlhausenOther nameActus tragicusOccasionFuneralBible text Acts 17:28 Psalms 90:12 Isaiah 38:1 Jesus Sirach 14:17 Revelation 22:20 Luke 18:31,34 Psalms 31:5 Chorale Ich hab mein Sach Gott heimgest...

Museum Sejarah NasionalΕθνικό Ιστορικό ΜουσείοDidirikan1882LokasiJalan Stadiou, Athena, YunaniJenisMuseum SejarahSitus webwww.nhmuseum.gr Museum Sejarah National (Yunani: Εθνικό Ιστορικό Μουσείο,[1] Ethnikó Istorikó Mouseío) merupakan sebuah museum sejarah di Athena. Didirikan pada tahun 1882, adalah yang tertua dari jenisnya di Yunani. Tempat ini terletak di Gedung Parlemen Lama di Jalan Stadiou, Athena, yang menjadi tempat Parlemen He...

حيوانات جزيرة الكنزどうぶつ宝島 (باليابانية) ملصقمعلومات عامةالتصنيف فيلم رسوم متحركة الصنف الفني أنيمي، حركة، مغامرات، كوميديا، فانتازياالموضوع قرصنة بحرية تاريخ الصدور 20 مارس، 1971 31 أكتوبر، 1973قالب:ايقونة علم مصر 15 نوفمبر، 2005 (دي في دي)مدة العرض 78 دقيقةاللغة الأصلية ياباني...

2017 song by BTS Mic DropCover for Steve Aoki remix featuring DesiignerSingle by BTS featuring Desiignerfrom the EP Love Yourself: Her ReleasedNovember 24, 2017 (2017-11-24)Genre Hip hop EDM trap Length3:58Label Big Hit Def Jam Virgin Songwriter(s) RM Supreme Boi Hitman Bang J-Hope Pdogg Steve Aoki Desiigner Tayla Parx Flowsik Shae Jacobs Producer(s)Pdogg (Korean and Japanese) Steve Aoki (Remix)BTS singles chronology DNA (2017) Mic Drop (2017) Fake Love (2018) Alternative ...

Referendum ending one-party rule in Malawi 1993 Malawian democracy referendum 14 June 1993 (1993-06-14) Results Choice Votes % One-party system 1,088,473 35.31% Multi-party system 1,993,996 64.69% Valid votes 3,082,469 97.75% Invalid or blank votes 70,979 2.25% Total votes 3,153,448 100.00% Registered voters/turnout 4,699,527 67.1% Results of the referendum by region (left) and district (right)Part of a series on Politics of Malawi Constitution Human rights Government President...

قرية البطيحى - قرية - تقسيم إداري البلد اليمن المحافظة محافظة حجة المديرية مديرية بني قيس الطور العزلة عزلة ربع الشمري السكان التعداد السكاني 2004 السكان 105 • الذكور 52 • الإناث 53 • عدد الأسر 15 • عدد المساكن 15 معلومات أخرى التوقيت توقيت اليمن (+3 �...

1800–1816 territory of the United States Not to be confused with Indian Territory. Territory of IndianaOrganized incorporated territory of the United States FlagCapitalVincennes (1800–1813)Corydon (1813–1816)Population • 1800 2,632• 1810 24,520• 1816 63,897 Government • TypeOrganized incorporated territoryGovernor • 1800–1812 William Henry Harrison• 1812–1813 John Gibson (acting)• 1813–1816 Thomas Posey Secretary ...

American politician (1798–1866) Francis L. HawksBornFrancis Lister Hawks(1798-06-10)June 10, 1798New Bern, North CarolinaDiedSeptember 26, 1866(1866-09-26) (aged 68)New York, New YorkAlma materNorth Carolina University Francis Lister Hawks (June 10, 1798 – September 26, 1866) was an American writer, historian, educator and priest of the Episcopal Church. After practicing law with some distinction (and a brief stint as politician in North Carolina), Hawks became an Episcopal prie...

Main article: George Washington General of the ArmiesGeorge WashingtonPortrait of George Washington in military uniform, painted by Rembrandt Peale, c. 1850Born(1732-02-22)February 22, 1732Westmoreland County, VirginiaDiedDecember 14, 1799(1799-12-14) (aged 67)Mount VernonAllegianceGreat BritainUnited StatesYears of service1752–1758 – British provincial militia 1775–1783 – Continental Army 1798–1799 – United States ArmyRankMajor 1752–1754 Lieutenant Col...

Johanna Uerieta Gertze (née Kazahendike) (Otjimbingwe, 16 July 1836 – 3 July 1935, Otjimbingwe) was a Namibian Herero and Christian convert. Gertze worked in the household of Carl Hugo Hahn and his wife at Otjikango. She initially came to the school at the mission to learn sewing and soon became so proficient that she was teaching the art to others. She appears to have been fluent in English, Dutch, and German, and she assisted in translating a variety of materials into Herero. Between 186...

ألة المزود مزود هو نوع موسيقي شعبي تونسي. وهو يعتبر جزءا من الثقافة التونسية. مكوّن من قربة أو ما يشبه الكيس المصنوع من الجلد وهي آلة هوائية ينفخ فيها العازف بواسطة مزمار والعادة ان تحتوي القربة على مزامير أخرى تأخد الهواء لاخراج صوت بعد الضغط على القربة وهي تستعمل كثيرا في ...

堀口九萬一 堀口 九萬一(ほりぐち くまいち、1865年2月23日〈元治2/慶応元年1月28日[1]〉 - 1945年〈昭和20年〉10月30日)は、日本の外交官(特命全権公使)、漢詩人、随筆家。号は長城。詩人・堀口大學の実父。 経歴 越後長岡藩の足軽(銃卒)堀口良次右衛門の長男として古志郡長岡城下に生まれる。北越戦争で旧暦明治元年6月に父が戦死[2]、翌年2月に幼く�...

此條目需要补充更多来源。 (2023年5月13日)请协助補充多方面可靠来源以改善这篇条目,无法查证的内容可能會因為异议提出而被移除。致使用者:请搜索一下条目的标题(来源搜索:集成电路设计 — 网页、新闻、书籍、学术、图像),以检查网络上是否存在该主题的更多可靠来源(判定指引)。 集成电路设计(英語:Integrated circuit design, IC design),多直稱IC設計,根据...