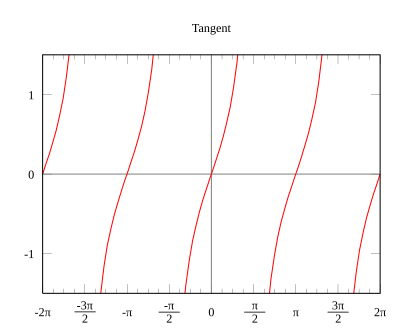
삼각 함수
|
Read other articles:

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Februari 2023. Perdana Menteri Trudeau dapat merujuk pada: Pierre Trudeau (1919–2000), Perdana Menteri Kanada ke-15 (1968–1979, 1980–1984) dan ayah dari Justin Trudeau Justin Trudeau (lahir 1971), Perdana Menteri Kanada ke-23 (sejak 2015) dan putra Pierre Trud...

PistoiaKomuneCittà di PistoiaThe Bell Tower of the Cathedral in Piazza Duomo.Negara ItaliaWilayahTuscanyProvinsiPistoia (PT)Frazionilihat listPemerintahan • Wali kotaRenzo Berti (mulai Mei 2002)Luas • Total236 km2 (91 sq mi)Ketinggian65 m (213 ft)Populasi (30 September 2008) • Total90.072 • Kepadatan380/km2 (990/sq mi)DemonimPistoiesiZona waktuUTC+1 (CET) • Musim panas (DST)UTC+2 (CEST)Kode po...

PicoPulauJulukan: Ilha PretaNegaraPortugalWilayah OtonomiAzoresPulauKelompok TengahLuas • Total447 km2 (173 sq mi) Pico adalah sebuah pulau di Portugal. Pulau ini terletak di bagian kepulauan Azores. Tepatnya di Samudra Pasifik. Dalam tradisi penyair Portugis, Raul Brandão, Pico disebut sebagai Ilha Preta (Pulau Hitam), untuk bumi vulkanik hitamnya, yang bertanggung jawab atas kebun-kebun anggur bersejarah yang ditunjuk-UNESCO yang memungkinkan pengembangan pu...

هذه صفحة مساعدة لكيفية عمل شيء ما.تفصّل هذه الصفحة طرق أو إجراءات بعض جوانب قواعد وممارسات ويكيبيديا. هذه الصفحة ليست واحدة من سياسات أو إرشادات ويكيبيديا، حيث لم تفحص بدقة عبر المجتمع. وصلات اللغات هي وصلات إنترويكي إلى نسخ اللغات الأخرى عن الموضوع نفسه ضمن نوع واحد من مشا...

CYTZCYYZCYKZCYZDCPZ9CNW8CTM4CNY8CPA5CPY5AHFBFDLFLALBAMATAWAclass=notpageimage| Location in the Toronto area. Historic airports code:AHF - Armour Heights FieldBF - Baker FieldDLF - De Lesseps FieldLA - Leaside AerodromeLBA - Long Branch AerodromeMA - Maple AerodromeTA - Toronto AerodromeWA - Willowdale Airfield Torontoclass=notpageimage| Location in Ontario Largest airports in the Greater Toronto AreaToronto Pearson International Airport served 47,130,358 passengers in 2017, making it the bus...

Questa voce sull'argomento centri abitati del Baden-Württemberg è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Sandhausencomune Sandhausen – Veduta LocalizzazioneStato Germania Land Baden-Württemberg DistrettoKarlsruhe CircondarioRhein-Neckar-Kreis TerritorioCoordinate49°20′38″N 8°39′29″E / 49.343889°N 8.658056°E49.343889; 8.658056 (Sandhausen)Coordinate: 49°20′38″N 8°39′29″E / 49....

Ni Ketut Mahadewi IstaraniInformasi pribadiKebangsaan IndonesiaLahir12 September 1994 (umur 29)Tabanan, Bali, IndonesiaTinggi162 m (531 ft 6 in)PeganganRightGanda putriPeringkat tertinggi13 (dengan Anggia Shitta Awanda 25 Januari 2018)Peringkat saat ini83 (dengan Tania Oktaviani Kusumah 3 Desember 2019) Rekam medali Bulu tangkis putri Mewakili Indonesia Piala Sudirman 2019 Nanning Tim campuran Pesta Olahraga Asia 2018 Jakarta-Palembang Tim putri Kejuar...

American marathon in Massachusetts 1970 Boston MarathonVenueBoston, Massachusetts, U.S.DateApril 20, 1970ChampionsMenRon Hill (2:10:30)WomenSara Mae Berman (3:05:07)← 19691971 → The 1970 Boston Marathon took place on Monday, April 20, 1970. It was the 74th time the Boston Marathon was organized, and featured 1,174 official entrants.[1] This was the first edition of the race to have a qualifying standard, as the entry form stipulated A runner must submit the certi...

この項目には、一部のコンピュータや閲覧ソフトで表示できない文字が含まれています(詳細)。 数字の大字(だいじ)は、漢数字の一種。通常用いる単純な字形の漢数字(小字)の代わりに同じ音の別の漢字を用いるものである。 概要 壱万円日本銀行券(「壱」が大字) 弐千円日本銀行券(「弐」が大字) 漢数字には「一」「二」「三」と続く小字と、「壱」「�...

第三十二届夏季奥林匹克运动会柔道比賽比賽場館日本武道館日期2021年7月24日至31日項目數15参赛选手393(含未上场5人)位選手,來自128(含未上场4队)個國家和地區← 20162024 → 2020年夏季奥林匹克运动会柔道比赛个人男子女子60公斤级48公斤级66公斤级52公斤级73公斤级57公斤级81公斤级63公斤级90公斤级70公斤级100公斤级78公斤级100公斤以上级78公斤以上级团体混...

Japanese professional wrestler For the football player, see Satoshi Yoneyama (footballer). Muhammad YoneYone in January 2020Birth nameSatoshi YoneyamaBorn (1976-02-23) February 23, 1976 (age 48)[1]Nagoya, Aichi, JapanProfessional wrestling careerRing name(s)Bichon Frise[2]Captain Noah[3]Muhammad YoneSatoshi Yoneyama[3]Billed height1.85 m (6 ft 1 in)[1]Billed weight110 kg (243 lb)[1]Trained byYoshiaki FujiwaraYuki Is...

Questa voce o sezione sull'argomento edizioni di competizioni calcistiche non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Segui i suggerimenti del progetto di riferimento. Campionato Interregionale 1990-1991 Competizione Campionato Interregionale Sport Calcio Edizione 43ª Organizzatore Lega Nazionale Dilettanti -Comitato per l'attività Interregionale L...

ASP WestwardIndustryNewspaperOwner1013 CommunicationsParentHearst Corporation Houston Community Newspapers (ASP Westward) Examiner Newspaper Group/The Rancher/Sugar Land Sun offices ASP Westward, L.P., or Westward,[1] was a local newspaper company, headquartered in Greenspoint, Houston.[2][3] It is owned by 1013 Communications of Reno, Nevada.[4] Houston Community Newspapers In Greater Houston ASP Westward did business as Houston Community Newspapers (HCN),[...

2016年美國總統選舉 ← 2012 2016年11月8日 2020 → 538個選舉人團席位獲勝需270票民意調查投票率55.7%[1][2] ▲ 0.8 % 获提名人 唐納·川普 希拉莉·克林頓 政党 共和黨 民主党 家鄉州 紐約州 紐約州 竞选搭档 迈克·彭斯 蒂姆·凱恩 选举人票 304[3][4][註 1] 227[5] 胜出州/省 30 + 緬-2 20 + DC 民選得票 62,984,828[6] 65,853,514[6]...

土库曼斯坦总统土库曼斯坦国徽土库曼斯坦总统旗現任谢尔达尔·别尔德穆哈梅多夫自2022年3月19日官邸阿什哈巴德总统府(Oguzkhan Presidential Palace)機關所在地阿什哈巴德任命者直接选举任期7年,可连选连任首任萨帕尔穆拉特·尼亚佐夫设立1991年10月27日 土库曼斯坦土库曼斯坦政府与政治 国家政府 土库曼斯坦宪法 国旗 国徽 国歌 立法機關(英语:National Council of Turkmenistan) ...

Puerto Vallartacomune Puerto Vallarta – Veduta LocalizzazioneStato Messico Stato federato Jalisco TerritorioCoordinate20°36′49″N 105°13′38″W / 20.613611°N 105.227222°W20.613611; -105.227222 (Puerto Vallarta)Coordinate: 20°36′49″N 105°13′38″W / 20.613611°N 105.227222°W20.613611; -105.227222 (Puerto Vallarta) Altitudine10 m s.l.m. Superficie52 km² Abitanti221 200 (2014) Densità4 253,85 ab./km² Al...

لمعانٍ أخرى، طالع أب (توضيح). أبمعلومات عامةصنف فرعي من والدانإنسان ذكر ممثلة بـ ذكر درجة القرابة 1 لديه جزء أو أجزاء legal father (en) الأب البيولوجيnon-biological father (en) النقيض أمولد تعديل - تعديل مصدري - تعديل ويكي بيانات الأبوة مسؤولية بطابع قدسي العلاقات(الخطوط العريضة) أنواع ا�...

Moisés Caicedo Moisés Caicedo con la camiseta del Brighton & Hove Albion F. C.Datos personalesNombre completo Moisés Isaac Caicedo CorozoNacimiento Santo Domingo, Ecuador2 de noviembre de 2001 (22 años)Nacionalidad(es) EcuatorianaAltura 1,78 m (5′ 10″)Peso 73 kg (161 lb)Carrera deportivaDeporte FútbolClub profesionalDebut deportivo 2019(Independiente del Valle)Club Chelsea F. C.Liga Premier LeaguePosición CentrocampistaDorsal(es) 25Goles en clubes 11Selecció...

Decumanus maximus di Palmira in Siria. Schema di base di un accampamento (castra) romano. Le porte erano quattro: la praetoria, verso il nemico (5); la decumana (7), ubicata sul lato opposto; la dextera (4) e la sinistra (6). Il decumanus maximus (2) collegava le porte praetoria e decumana, mentre il cardo maximus (3) la porta dextera a quella sinistra. In coincidenza del loro incrocio sorgeva solitamente il praetorium (1), che in seguito diveniva la sede del forum. Il decumano (in latino: de...

Pro-Spanish commerce raiders during the Dutch Revolt Witte de With's Action with Dunkirkers off Nieuwpoort in 1640 During the Dutch Revolt (1568–1648), the Dunkirkers or Dunkirk Privateers were commerce raiders in the service of the Spanish monarchy and later the Kingdom of France. They were also part of the Dunkirk fleet, which consequently was a part of the Spanish monarchy's Flemish fleet (Armada de Flandes). The Dunkirkers operated from the ports of the Flemish coast: Nieuwpoort, Ostend...