사상 (수학)
|
Read other articles:

The Right HonourableThe Lord Fellowes of West StaffordDL Lord TemporalPetahanaMulai menjabat 13 January 2011 Informasi pribadiLahirJulian Alexander Fellowes17 Agustus 1949 (umur 74)Kairo, MesirPartai politikKonservatifSuami/istriEmma Joy Kitchener (1990–sekarang)Anak1Alma materMagdalene, CambridgeWebber Douglas Academy of Dramatic ArtPekerjaanPemeran, novelis, penulis naskah, sutradaraSunting kotak info • L • B Julian Alexander Kitchener-Fellowes, Baron Fellowes of We...

Penerimaan Sakramen Penguatan di Jerman pada tahun 1679. Dalam gereja Katolik Roma, penguatan adalah salah satu dari tujuh sakramen.[1] Penguatan dipandang sebagai pemberian sumber kebijakan, pengetahuan dan keberanian bagi penerima, bila penerima menginginkannya dengan hati terbuka. Dan penguatan adalah pemenuhan dari kata Kristus yang berkata Dan kau akan tahu kebenaran dalam Kristus. (Yohanes 8:32). Secara umum di defenisikan sebagai pengetahuan dalam penguatan iman dalam lingkupan...

دوري أبطال أوروبا 2010–2011تفاصيل المسابقةالتواريخ29 يونيو 2010 – 28 مايو 2011الفرق32 (دور المجموعات)76 (المجموع) (من 52 اتحاد)المراكز النهائيةالبطل برشلونةالوصيف مانشيستر يونايتدإحصائيات المسابقةالمباريات الملعوبة213الأهداف المسجلة589 (2٫77 لكل مباراة)أفضل هداف ليونيل ميسي (12...

Основна́я теоре́ма о вы́четах — мощный инструмент для вычисления интеграла мероморфной функции по замкнутому контуру. Её часто используют также для вычисления вещественных интегралов. Она является обобщением интегральной теоремы Коши и интегральной формулы Коши. Illust...

Adam SandlerSandler di Festival Film Cannes 2017LahirAdam Richard Sandler9 September 1966 (umur 57)Brooklyn, New York, Amerika SerikatAlmamaterUniversitas New York (BFA)PekerjaanAktorkomedianpenulis skenarioproduserpenyanyiTahun aktif1987–sekarang[1]Partai politikRepublikSuami/istriJackie Titone (m. 2003)Anak2Karier komediMediaStand-upfilmtelevisimusikGenreKomedi observasionalKomedi musikalKomedi sketsaSatirSubjekBudaya Amerika SerikatKebuda...

Species of eucalyptus Yate Eucalyptus cornuta near Walpole Conservation status Near Threatened (IUCN 3.1)[1] Scientific classification Kingdom: Plantae Clade: Tracheophytes Clade: Angiosperms Clade: Eudicots Clade: Rosids Order: Myrtales Family: Myrtaceae Genus: Eucalyptus Species: E. cornuta Binomial name Eucalyptus cornutaLabill.[2] Synonyms[2] Eucalyptus macrocera Turcz. Eucalyptus cornuta, commonly known as yate,[3] is a tree species, sometimes a...

Pierluigi Casiraghi Pierluigi Casiraghi with Lazio in 1993.Informasi pribadiTanggal lahir 4 Maret 1969 (umur 55)Tempat lahir Monza, ItalyTinggi 182 m (597 ft 1 in)Posisi bermain PenyerangKarier senior*Tahun Tim Tampil (Gol)1985–1989 Monza 94 (28)1989–1993 Juventus 98 (20)1993–1998 Lazio 140 (41)1998–2000 Chelsea 10 (1)Total 342 (91)Tim nasional1991–1998 Italy 44 (13)Kepelatihan2002–2003 Monza (youth team)2003–2004 Legnano2006–2010 Italy U212014–2015 Cagl...

Wilayah Sheikh Jarrah. Di latar belakang, pusat kota Yerusalem. Sheikh Jarrah (Arab: الشيخ جراح, Ibrani: שייח' ג'ראח) adalah sebuah wilayah Palestina di Yerusalem Timur, yang berjarak 2 kilometer dari Kota Tua, di jalan menuju Gunung Scopus.[1][2] Wilayah tersebut mengambil nama dari makam abad ke-13 Sheikh Jarrah, seorang tabib Saladin, yang berada di wilayah tersebut. Wilayah modern didirikan pada 1865, dan secara bertahap menjadi pusat kediaman elit...

「俄亥俄」重定向至此。关于其他用法,请见「俄亥俄 (消歧义)」。 俄亥俄州 美國联邦州State of Ohio 州旗州徽綽號:七葉果之州地图中高亮部分为俄亥俄州坐标:38°27'N-41°58'N, 80°32'W-84°49'W国家 美國加入聯邦1803年3月1日,在1953年8月7日追溯頒定(第17个加入联邦)首府哥倫布(及最大城市)政府 • 州长(英语:List of Governors of {{{Name}}}]]) •&...

Northern Ireland politician Sinéád EnnisMLAEnnis in 2017Member of the Northern Ireland Assemblyfor South DownIncumbentAssumed office 3 March 2017Preceded byCaitríona Ruane Personal detailsBornDerryleckaghNationalityIrishPolitical partySinn FéinWebsiteSinéad Ennis MLA Sinéad Ennis is a Sinn Féin politician, elected to the Northern Ireland Assembly for the South Down constituency in the March 2017 elections.[1] She is married and has two daughters. She has played Gaelic games...

This article may require copy editing for grammar, style, cohesion, tone, or spelling. You can assist by editing it. (April 2024) (Learn how and when to remove this message) Tribal Mobilizationالحشد العشائريFounderThamer Al-TamimiCountryIraqSize25,000Part ofPopular Mobilization ForcesOpponents Islamic StateBattles and warsWar in Iraq (2013–2017) Tribal Mobilization or Tribal Fighters are an Iraqi Sunni tribal group composed of members of tribes to fight against the Islami...

School district in Pennsylvania, United States Abington School DistrictAddress970 Highland Avenue Abington, Pennsylvania, 19001United StatesCoordinates40°06′43″N 75°07′41″W / 40.112°N 75.128°W / 40.112; -75.128District informationTypePublic school districtGradesK-12PresidentShameeka BrownSuperintendentDr. Jeffery S. FecherNCES District ID4202040[1]Students and staffEnrollment8,543[1]Teachers592[1]Staff622[1]Student–teacher ...
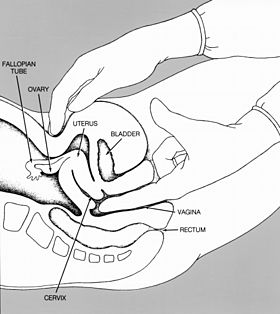
هذه المقالة تحتاج للمزيد من الوصلات للمقالات الأخرى للمساعدة في ترابط مقالات الموسوعة. فضلًا ساعد في تحسين هذه المقالة بإضافة وصلات إلى المقالات المتعلقة بها الموجودة في النص الحالي. (سبتمبر 2016) فحص الحوض رسم بياني يوضح طريقة الجس المُتبعة في فحص الحوض. معلومات عامة الاختص...

Antisemitic and anti-LGBT hate crime Murder of Blaze BernsteinPart of antisemitism in the United States and violence against LGBT people in the United StatesBernsteinLocationLake Forest, California, U.S.DateJanuary 2, 2018; 6 years ago (2018-01-02) PST (UTC-08:00)Attack typeMurder by stabbing, hate crimeVictimBlaze Bernstein, aged 19Accused1ChargesFirst-degree murder On January 10, 2018, 19-year-old University of Pennsylvania sophomore Blaze Bernstein was found dead in a par...

Chemical compound Not to be confused with 17α-hydroxyprogesterone. 11α-HydroxyprogesteroneClinical dataOther names11α-OHP; 11α-Hydroxypregn-4-ene-3,20-dione; 4-Pregnen-11α-ol-3,20-dione; δ4-Pregnen-11α-ol-3,20-dioneIdentifiers IUPAC name (8S,9S,10R,11R,13S,14S,17S)-17-acetyl-11-hydroxy-10,13-dimethyl-1,2,6,7,8,9,11,12,14,15,16,17-dodecahydrocyclopenta[a]phenanthren-3-one CAS Number80-75-1 YPubChem CID92730ChemSpider83709UNIID8X4JXL4VMChEBICHEBI:16076ChEMBLChEMBL1563246CompTox Dash...

Summa de arithmeticaTitolo originaleSumma de arithmetica, geometria, proportioni et proportionalita' Titelbladet till Summa de arithmetica ... AutoreLuca Pacioli 1ª ed. originale1494 Generetrattato Sottogenerematematica Lingua originalelatino Modifica dati su Wikidata · Manuale La Summa de arithmetica, geometria, proportioni et proportionalita (Riassunto dell'aritmetica, geometria, proporzioni e proporzionalità) è un libro di matematica scritto da Luca Pacioli (1445-1517) e pubblicat...

Skyscraper in London, England This article is about the London skyscraper. For the pickled cucumber, see Gherkin. The GherkinSeen from Leadenhall StreetAlternative names30 St Mary Axe / the Swiss Re BuildingGeneral informationStatusCompletedTypeOfficeArchitectural styleNeo-futuristic / hi-tech / post-modernLocation30 St Mary Axe,London, EC3[1][2]Coordinates51°30′52″N 00°04′49″W / 51.51444°N 0.08028°W / 51.51444; -0.08028Construction started2...

Award for an American football player Not to be confused with Super Bowl Most Valuable Player Award. Peyton Manning was named AP NFL MVP five times, more than any other player in history. The National Football League Most Valuable Player Award (NFL MVP) is an award given by various entities to the American football player who is considered the most valuable in the National Football League (NFL) during the regular season. Organizations which issue an NFL MVP award include the Associated Press ...

Public research university in Bozeman, Montana, U.S. Montana State redirects here. For the U.S. state, see Montana. This article is about the main campus in Bozeman. For other campuses, see Montana University System. Montana State UniversityFormer nameAgricultural College of the State of Montana (1893–1913)Montana College of Agriculture and Mechanic Arts (1913–1965)MottoMountains & MindsTypePublic land-grant research universityEstablished8 November 1893; 130 years ago (8 ...

Scottish papermaker (1775–1859) Alexander CowanBorn(1775-06-17)17 June 1775Penicuik, ScotlandDied13 February 1859(1859-02-13) (aged 83)OccupationPapermaker Portrait head of Alexander Cowan Alexander Cowan (17 June 1775 – 13 February 1859) was a Scottish papermaker and philanthropist. He was the 13th child and third surviving son of Charles Cowan (8 June 1735 – 23 February 1805) and Marjory Cowan nee Fidler (16 July 1734 – 30 November 1819) He was also a cousin and friend of Thoma...

































