방정식
|
Read other articles:

Artikel ini bukan mengenai Miss International atau InterContinental Hotels Group. Miss IntercontinentalLogo Miss IntercontinentalSingkatanMIOMICTanggal pendirian1973; 51 tahun lalu (1973)(Sebagai Miss Teenage Peace International)PendiriAtan Lee(Sebagai Miss Teenage Peace International)Didirikan diOranjestad, ArubaTipeKontes kecantikanKantor pusatPanama City, PanamaWilayah layanan InternasionalJumlah anggota lebih dari 80 negaraBahasa resmi InggrisPresidenManoj Chatlani(Sejak 2016)Tokoh p...

Funeral of Syrian President Hafez al-Assad Death and state funeral of Hafez al-AssadOfficial portrait of Hafez al-AssadDate13 June 2000; 23 years ago (2000-06-13)LocationDamascus, SyriaParticipantsSyrian officials and dignitaries from foreign countries Hafez al-Assad, the 18th president of Syria, died from a heart attack on 10 June 2000 at the age of 69.[1][2] His funeral was held three days later in Damascus, and he was buried in a mausoleum in his hometown ...

Dakotaraptor TaksonomiDivisiManiraptoriformesSubdivisiManiraptoraKladPennaraptoraKladParavesInfradivisiDeinonychosauriaFamiliDromaeosauridaeSubfamiliEudromaeosauriaTribusDromaeosaurinaeGenusDakotaraptor Robert DePalma, 2015 lbs Dakotaraptor adalah sebuah genus teropoda dromaeosaurid karnivora dari Zaman Kapur Akhir di Amerika Utara. Fosil pertama Dakotaraptor ditemukan di Dakota Selatan, Amerika Serikat pada 2005. Referensi Templat:Dromaeosauridae Pengidentifikasi takson Wikidata: Q21282866 E...

العلاقات الغواتيمالية الميانمارية غواتيمالا ميانمار غواتيمالا ميانمار تعديل مصدري - تعديل العلاقات الغواتيمالية الميانمارية هي العلاقات الثنائية التي تجمع بين غواتيمالا وميانمار.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعي...

Polish politician Tomasz TomczykiewiczParliamentary Leader of the Civic Platform8th Leader of the Civic Platform in the SejmIn office22 July 2010 – 7 November 2011LeaderDonald TuskPreceded byGrzegorz SchetynaSucceeded byRafał GrupińskiMember of Sejm4th Parliament • 5th Parliament • 6th ParliamentIn office19 October 2001 – 28 November 2015 Personal detailsBornTomasz Kazimierz Tomczykiewicz(1961-03-02)2 March 1961Pszczyna, PolandDied28 November 2015(2015-11-28) (aged...
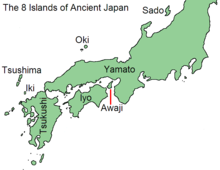
Izanagi and Izanami. Painting by Kobayashi Eitaku, c. 1885. In Shinto chronology, the Age of the Gods (神代, Kami-yo/Jindai) is the period preceding the accession of Jimmu, the first Emperor of Japan.[1] The kamiyo myths are chronicled in the upper roll (Kamitsumaki) of the Kojiki and in the first and second chapters of the Nihon Shoki. The reigns of Emperor Jimmu and the subsequent Emperors are considered the Human Age (人代, Hitoyo). Origin See also: Japanese creation myth Accor...

Línea 1 - Azul Vista de la estación Parada Inglesa.LugarUbicación São Paulo, BrasilÁrea abastecida Bom RetiroJabaquaraLibertadeSantanaSaúdeSéTucuruviVila MarianaDescripciónTipo MetroSistema Metro de São PauloInauguración 14 de septiembre de 1974 (49 años)Inicio TucuruviFin JabaquaraIntercambiadores Ana Rosa Paraíso Sé Luz Santa CruzDepósitos 1 (Jabaquara)Características técnicasLongitud 20,2 kmVías 2Estaciones 23Ancho de vía 1600 mmElectrificación 750 V CC por Tercer ...
Unincorporated community in Pennsylvania, United StatesHarmarville, PennsylvaniaUnincorporated communityHarmarvilleLocation within the U.S. state of PennsylvaniaCoordinates: 40°32′5″N 79°51′8″W / 40.53472°N 79.85222°W / 40.53472; -79.85222CountryUnited StatesStatePennsylvaniaCountyAlleghenyTownshipHarmarTime zoneUTC-5 (Eastern (EST)) • Summer (DST)UTC-4 (EDT) Harmarville is an unincorporated community located in Harmar Township, Allegheny Count...

British television detective series (2002–2015) Foyle's WarGenre Mystery War Period drama Created byAnthony HorowitzStarring Michael Kitchen Honeysuckle Weeks Anthony Howell Opening themeJim ParkerCountry of originUnited KingdomOriginal languageEnglishNo. of series8No. of episodes28ProductionExecutive producerJill GreenProducers Jill Green Simon Passmore (2002–2003) Keith Thompson (2004–2006) Running time86–100 minutesProduction companiesGreenlit Productions (seasons 1-6)Eleventh Hour...

2016年美國總統選舉 ← 2012 2016年11月8日 2020 → 538個選舉人團席位獲勝需270票民意調查投票率55.7%[1][2] ▲ 0.8 % 获提名人 唐納·川普 希拉莉·克林頓 政党 共和黨 民主党 家鄉州 紐約州 紐約州 竞选搭档 迈克·彭斯 蒂姆·凱恩 选举人票 304[3][4][註 1] 227[5] 胜出州/省 30 + 緬-2 20 + DC 民選得票 62,984,828[6] 65,853,514[6]...

此条目序言章节没有充分总结全文内容要点。 (2019年3月21日)请考虑扩充序言,清晰概述条目所有重點。请在条目的讨论页讨论此问题。 哈萨克斯坦總統哈薩克總統旗現任Қасым-Жомарт Кемелұлы Тоқаев卡瑟姆若马尔特·托卡耶夫自2019年3月20日在任任期7年首任努尔苏丹·纳扎尔巴耶夫设立1990年4月24日(哈薩克蘇維埃社會主義共和國總統) 哈萨克斯坦 哈萨克斯坦政府...

American metalcore band This article may contain an excessive amount of intricate detail that may interest only a particular audience. Please help by spinning off or relocating any relevant information, and removing excessive detail that may be against Wikipedia's inclusion policy. (April 2021) (Learn how and when to remove this message) Poison the WellJeffery Moreira, England, 2007Background informationAlso known asDoubting Thomas, An Acre LostOriginCoral Springs, Florida, United StatesGenre...

Defamation case in Australia against Google Google LLC v DefterosCourtHigh Court of AustraliaDecided17 August 2022 (appeal) 30 April 2020 (initial)Citation(s)[2022] HCA (appeal) [2020] VSC 219 (initial)Case historyAppealed fromSupreme Court of VictoriaKeywordsDefamationHyperlinkSearch engineGoogle Google LLC v Defteros was a defamation case in Australia brought by a lawyer against Google. George Defteros is a lawyer, with much of his work being representing defendant gang memb...

Generalization of mass, length, area and volume For the coalgebraic concept, see Measuring coalgebra. Not to be confused with Metric (mathematics). This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (January 2021) (Learn how and when to remove this message) Informally, a measure has the property of being monotone in the sense that if A {\displaystyle A} is a subs...

الدوري السوفييتي الممتاز الجهة المنظمة الاتحاد السوفيتي لكرة القدم تاريخ الإنشاء 22 مايو 1936 الرياضة كرة القدم البلد الاتحاد السوفيتي انتهى 1991 أحدث بطل سسكا موسكو (اللقب السابع) (1991) الأكثر فوزا دينامو كييف (13 لقباً) يتأهل إلى دوري أبطال أوروبا كأس الكؤوس الأوروبية...

For other uses, see Anerley (disambiguation). Town in EnglandAnerleyTownAnerley Road 2010AnerleyLocation within Greater LondonOS grid referenceTQ345695• Charing Cross7.0 mi (11.3 km) NNWLondon boroughBromleyCeremonial countyGreater LondonRegionLondonCountryEnglandSovereign stateUnited KingdomPost townLONDONPostcode districtSE20Dialling code020PoliceMetropolitanFireLondonAmbulanceLondon UK ParliamentBeckenham and PengeLondon As...

2019 studio album by Hiroko MoriguchiGundam Song CoversStudio album by Hiroko MoriguchiReleasedAugust 7, 2019 (2019-08-07)Recorded2015–2019StudioBellwood RecordsDutchmama StudioKing Sekiguchidai StudioSound Inn StudioVictor StudioGenreJ-popjazzanisonLength54:34LanguageJapaneseLabelKing RecordsProducerDaisuke SohkawaHiroko Moriguchi chronology Perfect Best(2013) Gundam Song Covers(2019) Gundam Song Covers 2(2020) Alternative cover Music videoGundam Song Covers all song...

Disambiguazione – Se stai cercando il romanzo, vedi Regina di Saba (romanzo). Disambiguazione – Regina del Sud rimanda qui. Se stai cercando la serie televisiva, vedi Regina del Sud (serie televisiva). La regina di Saba (1907), di Edward Slocombe. Regina di Saba è un'espressione antonomastica che si riferisce a una specifica sovrana del Regno di Saba, citata nella Bibbia (primo libro dei Re, e nel secondo libro delle Cronache), nel Corano e nel Kebra Nagast. Nei testi biblici e ...

العلاقات الإيطالية الميانمارية إيطاليا ميانمار إيطاليا ميانمار تعديل مصدري - تعديل العلاقات الإيطالية الميانمارية هي العلاقات الثنائية التي تجمع بين إيطاليا وميانمار.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية للدولتين: و�...

Chinese politician (1938–2007) In this Chinese name, the family name is Huang. Huang Ju黄菊Huang Ju in 2005First-ranked Vice Premier of ChinaIn office15 March 2003 – 2 June 2007PremierWen JiabaoPreceded byLi LanqingSucceeded byWu Yi (Acting)Communist Party Secretary of ShanghaiIn office28 September 1994 – 22 October 2002DeputyXu Kuangdi (mayor)Preceded byWu BangguoSucceeded byChen LiangyuMayor of ShanghaiIn office29 April 1991 – 24 February 1994LeaderWu Ba...





























