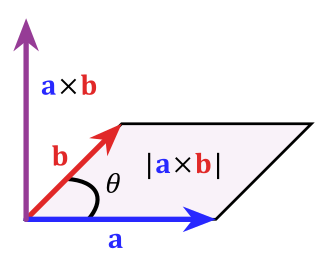
クロス積
|
Read other articles:

Italian association football club based in Naples Football clubNapoliFull nameSocietà Sportiva Calcio Napoli S.p.A.Nickname(s)Gli Azzurri (The Blues)I Partenopei (The Parthenopeans)I Ciucciarelli (The Little Donkeys)Short nameSSC NapoliFounded25 August 1926; 97 years ago (25 August 1926), as Associazione Calcio Napoli 6 September 2004; 19 years ago (6 September 2004), as Napoli SoccerGroundStadio Diego Armando MaradonaCapacity54,725OwnerAurelio De LaurentiisPresiden...

Final Liga Champions UEFA 2015Berkas:Final Liga Champions UEFA programme.jpgTurnamenLiga Champions UEFA 2014–15 Juventus Barcelona 1 3 Tanggal6 Juni 2015StadionStadion Olimpiade Berlin, BerlinPemain Terbaik Andrés Iniesta (Barcelona)[1]WasitCüneyt Çakır (Turkey)Penonton70.442[2]CuacaSetengah berawan26 °C (79 °F)49% Kelembaban relatif[3]← 2014 2016 → Final Liga Champions UEFA 2015 akan menjadi pertandingan final bagi Liga Champions UEFA 201...

Laksamana TNI (Purn.)Ricardus Subono Duta Besar Indonesia untuk Britania Raya ke-8Masa jabatan1974–1978PresidenSoeharto PendahuluRusmin NuryadinPenggantiSaleh BasarahKepala Staf TNI Angkatan Laut ke-7Masa jabatan26 Juni 1973 – 26 Juni 1974PresidenSoeharto PendahuluSudomoPenggantiR.S. Subijakto Informasi pribadiLahir(1927-06-27)27 Juni 1927Yogyakarta, Hindia BelandaMeninggal8 Februari 1992(1992-02-08) (umur 64)Jakarta, IndonesiaKebangsaan IndonesiaProfesiTentaraK...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (يوليو 2019) فريدريك بيري (بالألمانية: Friedrich Bury) معلومات شخصية الميلاد 21 مارس 1763 هاناو الوفاة 18 مايو 1823 (60 سنة) [1][2] آخن مواطنة انتخابية هسن ...

Flat woven decorative knot Carrick matCarrick mat made with three passesNamesCarrick mat, Prolong knotCategoryDecorativeRelatedCarrick bend, Turk's head, Austrian knotTypical useMat for padding or decorationABoK#2242, #2244Instructions[1] Carrick mats on schooner Adventuress, used to protect woodwork from the blocks when the lines are slack. 818 knotBasic seamless formArf invariant1Braid length8Braid no.3Bridge no.3Crosscap no.4Crossing no.8Genus3Hyperbolic volume12.35090621Unknotting no.2Con...

Harmandir Sahib di Amritsar, India, merupakan gurdwara tersuci dalam kepercayaan Sikhisme. Gurdwara (bahasa Punjabi: ਗੁਰਦੁਆਰਾ, Guruduārā atau ਗੁਰਦਵਾਰਾ, gurudwārā; berarti pintu menuju Guru) adalah tempat ibadah orang-orang Sikh. Orang-orang yang menganut kepercayaan lain atau yang tidak beriman juga diterima di tempat ini. Setiap gurdwara memiliki sebuah Darbar Sahib; di situ guru abadi dan kitab suci Sikh Guru Granth Sahib ditempatkan di atas sebuah ta...

River in northern Sweden and Finland For the river in Lincolnshire and South Yorkshire, England, see River Torne (England). For the Japanese PlayStation 3 accessory, see PlayTV § torne. Torne riverTornionjoki (Finnish)Torne älv/Torneälven (Swedish)Duortneseatnu (Northern Sami)Väylä (Meänkieli)The Torne at Kukkola rapids north of TornioLocation of the TorneLocationCountriesSwedenFinlandNorway (hydrological source)Physical characteristicsSourceTorne träsk an...

El texto que sigue es una traducción defectuosa. Si quieres colaborar con Wikipedia, busca el artículo original y mejora esta traducción.Copia y pega el siguiente código en la página de discusión del autor de este artículo: {{subst:Aviso mal traducido|Fuerza Aérea Árabe Siria}} ~~~~ Fuerza Aérea Árabe Siria قوات الجوية العربية السوريةAl Quwwat al-Jawwiyah al Arabiya as-SouriyaActiva 1948País SiriaTipo Fuerza aéreaTamaño 60 000 efectivosParte d...

この項目には、一部のコンピュータや閲覧ソフトで表示できない文字が含まれています(詳細)。 数字の大字(だいじ)は、漢数字の一種。通常用いる単純な字形の漢数字(小字)の代わりに同じ音の別の漢字を用いるものである。 概要 壱万円日本銀行券(「壱」が大字) 弐千円日本銀行券(「弐」が大字) 漢数字には「一」「二」「三」と続く小字と、「壱」「�...

Sungai Seberang Mesjid 1aSungai Seberang Mesjid 1aLokasiNegaraIndonesiaProvinsiKalimantan SelatanCiri-ciri fisikHulu sungai - lokasiKalimantan Muara sungaiSungai MartapuraPanjang137,989 m Sungai Seberang Mesjid 1a adalah sungai yang mengalir di kota Banjarmasin, Kalimantan Selatan, Indonesia. Geografi Sungai ini mengalir di kelurahan Seberang Mesjid, kecamatan Banjarmasin Tengah, Kota Banjarmasin dan bermuara ke Sungai Martapura.[1] Sungai Seberang Mesjid 1a memiliki p...

Pour les articles homonymes, voir Gray. Loren GrayBiographieNaissance 19 avril 2002 (22 ans)PottstownNom de naissance AchonchonNationalité américaineActivités Chanteuse, youtubeuse, productrice de télévisionPériode d'activité depuis 2015Autres informationsLabel Virgin MusicDistinction Forbes 30 Under 30 (2021)modifier - modifier le code - modifier Wikidata Loren Gray Beech, née le 19 avril 2002, est une influenceuse, chanteuse, vidéaste et femme d'affaires américaine. Biograph...

Agricultural wetland region in northern Israel This article is about a valley in Israel. For the region in Syria, see Houla. For the town in Lebanon, see Hula, Lebanon. Designations Ramsar WetlandOfficial nameHula Nature ReserveDesignated12 November 1996; 27 years ago (1996-11-12)Reference no.868[1] A wheat field in the Hula Valley, against the background of Mount Hermon, March 2007. Hula Valley farmland The Hula Valley (Hebrew: עמק החולה, Modern: E...

1991 studio album by Diana RossThe Force Behind the PowerStudio album by Diana RossReleasedSeptember 10, 1991GenreNew jack swingR&BLength47:3356:51LabelMotownProducerStevie WonderAl B. Sure!James Anthony CarmichaelPeter AsherDiana Ross chronology Greatest Hits Live(1989) The Force Behind the Power(1991) Stolen Moments: The Lady Sings... Jazz and Blues(1993) Singles from The Force Behind the Power If We Hold on TogetherReleased: November 5, 1988 No Matter What You Do (Duet w/ Al B....

سك على إخواتك النوع كوميدي تأليف كريم فهمي إخراج وائل إحسان بطولة علي ربيع ، صلاح عبد الله ، سلوى خطاب ،هنا الزاهد ،كريم عفيفي البلد مصر لغة العمل العربية عدد الحلقات 30 مدة الحلقة 40 دقيقة منتج سيدرز آرت برودكشن (صباح إخوان) صادق الصباح بث لأول مرة في 1 رمضان 1439هـ 17 ماي 2018...

British politician (born 1937) The Right HonourableThe Lord MacGregor of Pulham MarketOBE PC FKCParliamentary portrait, 2018 Ministerial Offices 1979–1994 Secretary of State for TransportIn office11 April 1992 – 20 July 1994Prime MinisterJohn MajorPreceded byMalcolm RifkindSucceeded byBrian MawhinneyLeader of the House of CommonsLord President of the CouncilIn office2 November 1990 – 11 April 1992Prime MinisterMargaret ThatcherJohn MajorPreceded byGeoffrey Howe...

Se ha sugerido que esta página sea renombrada como «Universidad Harvard». Motivo: los argumentos están expuestos en la página de discusión. «Harvard» redirige aquí. Para otras acepciones, véase Harvard (desambiguación). Universidad de Harvard Harvard University Escudo de la Universidad de Harvard La Escuela de negocios Harvard (izquierda), Harvard Kennedy School (derecha) y Weeks Footbridge al atardecer.Sigla H.U.Lema Veritas«Verdad»Tipo Universidad privadaFundación 8 de septie...

2021 MMA event UFC 260: Miocic vs. Ngannou 2The poster for UFC 260: Miocic vs. Ngannou 2InformationPromotionUltimate Fighting ChampionshipDateMarch 27, 2021 (2021-03-27)VenueUFC ApexCityEnterprise, Nevada, United StatesAttendanceNone (behind closed doors)[1]Event chronology UFC on ESPN: Brunson vs. Holland UFC 260: Miocic vs. Ngannou 2 UFC on ABC: Vettori vs. Holland UFC 260: Miocic vs. Ngannou 2 was a mixed martial arts event produced by the Ultimate Fighting Champions...

For the article about the 1961 film adaptation, see The Children's Hour (film). 1934 play by Lillian Hellman The Children's HourFirst edition 1934Written byLillian HellmanCharacters Evelyn Munn Mrs Lily Mortar Peggy Rogers Helen Burton Lois Fisher Catherine Rosalie Wells Mary Tilford Karen Wright Martha Dobie Doctor Joseph Cardin Agatha Mrs Amelia Tilford A Grocery Boy Date premieredNovember 20, 1934 (1934-11-20)Place premieredMaxine Elliott Theatre, New York CityOriginal langu...

Artikel ini perlu dikembangkan agar dapat memenuhi kriteria sebagai entri Wikipedia.Bantulah untuk mengembangkan artikel ini. Jika tidak dikembangkan, artikel ini akan dihapus. Halaman awal edisi 1604 Altan Tobchi (Aksara Mongol: ᠠᠯᠲᠠᠨ ᠲᠣᠪᠴᠢ Altan Tobči;[1] Kiril Mongol: Алтан товч, Altan tovch) adalah sebuah cerita kronik Mongolia pada abad ke-17. Di dalamnya terdapat beberapa kisah, di antaranya: menuduh istrinya selingkuh dan terjadinya pembunuhan. Ref...

2014 Hong Kong political movement This article is about the political movement in Hong Kong. For related protests in Hong Kong also known as the Umbrella Revolution, see 2014 Hong Kong protests. For the 2019 book, see The Umbrella Movement: Civil Resistance and Contentious Space in Hong Kong. This article needs to be updated. The reason given is: Portions of the article are written in the present tense. Please help update this article to reflect recent events or newly available information. (...

![{\displaystyle [{\boldsymbol {a}},{\boldsymbol {b}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b9312534b1ba4c99e32566a32c071977ddad384b)









![{\displaystyle [{\boldsymbol {a}},{\boldsymbol {b}}]_{1}=({\boldsymbol {e}}_{1},[{\boldsymbol {a}},{\boldsymbol {b}}])={\begin{vmatrix}1&a_{1}&b_{1}\\0&a_{2}&b_{2}\\0&a_{3}&b_{3}\\\end{vmatrix}}=a_{2}b_{3}-a_{3}b_{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4349b2fce366207e757ca54392f753a52fc9da0d)
![{\displaystyle [{\boldsymbol {a}},{\boldsymbol {b}}]_{2}=({\boldsymbol {e}}_{2},[{\boldsymbol {a}},{\boldsymbol {b}}])={\begin{vmatrix}0&a_{1}&b_{1}\\1&a_{2}&b_{2}\\0&a_{3}&b_{3}\\\end{vmatrix}}=a_{3}b_{1}-a_{1}b_{3}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e1511f42e28b2c8732131ea0bb027b684aa993e2)
![{\displaystyle [{\boldsymbol {a}},{\boldsymbol {b}}]_{3}=({\boldsymbol {e}}_{3},[{\boldsymbol {a}},{\boldsymbol {b}}])={\begin{vmatrix}0&a_{1}&b_{1}\\0&a_{2}&b_{2}\\1&a_{3}&b_{3}\\\end{vmatrix}}=a_{1}b_{2}-a_{2}b_{1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f9f0207a5c8f10efb689e85cd510d213bb15f162)
![{\displaystyle [{\boldsymbol {a}},{\boldsymbol {b}}]\doteq {\begin{pmatrix}a_{2}b_{3}-a_{3}b_{2}\\a_{3}b_{1}-a_{1}b_{3}\\a_{1}b_{2}-a_{2}b_{1}\\\end{pmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/52d2a2643983ecdda9538f4b90fb3cc53f0423f4)
![{\displaystyle [{\boldsymbol {a}},{\boldsymbol {b}}]={\begin{vmatrix}{\boldsymbol {e}}_{1}&a_{1}&b_{1}\\{\boldsymbol {e}}_{2}&a_{2}&b_{2}\\{\boldsymbol {e}}_{3}&a_{3}&b_{3}\end{vmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ecdc5222d6868cc91016a795adf8011d2b9f5bf)
![{\displaystyle [{\boldsymbol {a}},{\boldsymbol {b}}]_{i}=\sum _{j,k}\epsilon _{ijk}a_{j}b_{k}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f2e2b0ca64f606d305621506a8566769c3b6f6a6)




![{\displaystyle [{\boldsymbol {a}},{\boldsymbol {a}}]={\boldsymbol {0}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/de09f61713ceb571793a08c86640e65fca795744)


![{\displaystyle [{\boldsymbol {a}},k{\boldsymbol {b}}+l{\boldsymbol {c}}]=k[{\boldsymbol {a}},{\boldsymbol {b}}]+l[{\boldsymbol {a}},{\boldsymbol {c}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e1a89fae470f1fdcdca0259bb3136f179e7982f0)
![{\displaystyle [k{\boldsymbol {b}}+l{\boldsymbol {c}},{\boldsymbol {a}}]=k[{\boldsymbol {b}},{\boldsymbol {a}}]+l[{\boldsymbol {c}},{\boldsymbol {a}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b9c73e1f490b1534bc0d5a0dd98af0735a19ced7)
![{\displaystyle [{\boldsymbol {a}},{\boldsymbol {0}}]=[{\boldsymbol {0}},{\boldsymbol {a}}]={\boldsymbol {0}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/90fd83f7cab062ccbe03547df7ef0dbc69b29d75)
![{\displaystyle [{\boldsymbol {a}},[{\boldsymbol {b}},{\boldsymbol {c}}]]=({\boldsymbol {a}},{\boldsymbol {c}})\,{\boldsymbol {b}}-({\boldsymbol {a}},{\boldsymbol {b}})\,{\boldsymbol {c}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ac7503be70399904420db5aeeba3d86b227bd75c)
![{\displaystyle [{\boldsymbol {a}},[{\boldsymbol {b}},{\boldsymbol {c}}]]-[[{\boldsymbol {a}},{\boldsymbol {b}}],{\boldsymbol {c}}]\neq {\boldsymbol {0}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fe4ad1428e449a33b245c7890946b37a4bea4ca4)
![{\displaystyle [{\boldsymbol {a}},[{\boldsymbol {b}},{\boldsymbol {c}}]]-[[{\boldsymbol {a}},{\boldsymbol {b}}],{\boldsymbol {c}}]=[{\boldsymbol {b}},[{\boldsymbol {a}},{\boldsymbol {c}}]]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9e2a27c9dfd413efb3160594702c7b452389b76d)
![{\displaystyle [{\boldsymbol {a}},[{\boldsymbol {b}},{\boldsymbol {c}}]]+[{\boldsymbol {b}},[{\boldsymbol {c}},{\boldsymbol {a}}]]+[{\boldsymbol {c}},[{\boldsymbol {a}},{\boldsymbol {b}}]]={\boldsymbol {0}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/56d607faf2e8a034576fcf65d9632c1dc5c1853e)






![{\displaystyle ({\boldsymbol {v}},[{\boldsymbol {a}}_{1},\ldots ,{\boldsymbol {a}}_{n-1}])=\det \langle {\boldsymbol {v}},{\boldsymbol {a}}_{1},\ldots ,{\boldsymbol {a}}_{n-1}\rangle }](https://wikimedia.org/api/rest_v1/media/math/render/svg/5c7f2ed5805dda8d32ec655e9e7c00f0591e4be8)
![{\displaystyle [{\boldsymbol {a}}_{1},\ldots ,{\boldsymbol {a}}_{n-1}]_{i}=\sum _{j_{1},\ldots ,j_{n-1}}\epsilon _{i,j_{1},\ldots ,j_{n-1}}a_{1}^{j_{1}}\cdots a_{n-1}^{j_{n-1}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1849fb2030deceaab3a16064c64f671236ab5ec6)
![{\displaystyle [{\boldsymbol {a}}]={\begin{pmatrix}a_{2}\\-a_{1}\\\end{pmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ffd2fada44669d3c8511498290b506659f8e4891)
![{\displaystyle [{\boldsymbol {a}},{\boldsymbol {b}},{\boldsymbol {c}}]={\begin{pmatrix}+a_{2}b_{3}c_{4}+a_{3}b_{4}c_{2}+a_{4}b_{2}c_{3}-a_{2}b_{4}c_{3}-a_{3}b_{2}c_{4}-a_{4}b_{3}c_{2}\\-a_{3}b_{4}c_{1}-a_{4}b_{1}c_{3}-a_{1}b_{3}c_{4}+a_{3}b_{1}c_{4}+a_{4}b_{3}c_{1}+a_{1}b_{4}c_{3}\\+a_{4}b_{1}c_{2}+a_{1}b_{2}c_{4}+a_{2}b_{4}c_{1}-a_{4}b_{2}c_{1}-a_{1}b_{4}c_{2}-a_{2}b_{1}c_{4}\\-a_{1}b_{2}c_{3}-a_{2}b_{3}c_{1}-a_{3}b_{1}c_{2}+a_{1}b_{3}c_{2}+a_{2}b_{1}c_{3}+a_{3}b_{2}c_{1}\\\end{pmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e21e567381f509202aa3e7ffd6841c1297e8f9e0)











