黒板太字
|
Read other articles:

1988-93 seating of the national legislature of the North American country 34th Parliament of CanadaMajority parliament12 December 1988 – 8 September 1993Parliament leadersPrimeMinisterRt. Hon. Brian MulroneySeptember 17, 1984 (1984-09-17) – June 25, 1993 (1993-06-25)Rt. Hon. Kim CampbellJune 25, 1993 (1993-06-25) – November 4, 1993 (1993-11-04)Cabinets24th Canadian Ministry25th Canadian MinistryLeader of theOp...

I Want to Know What Love IsLagu oleh Foreignerdari album Agent ProvocateurSisi-BStreet Thunder (Marathon Theme)Dirilis13 November 1984Format7GenrePop rock, soft rockDurasi5:00 (album/7 single) 6:23 (12 single)4:15 (radio edit/berbagai versi sunting)LabelAtlanticPenciptaMick JonesProduserMick Jones, Alex SadkinSampel Musik I Want to Know What Love Is noiconnoicon I Want to Know What Love Is adalah sebuah power ballad karya band rock Inggris-Amerika Foreigner. Lagu tersebut dirilis pada Novembe...

Jangilus Status konservasi Risiko Rendah (IUCN 3.1)[1] Klasifikasi ilmiah Kerajaan: Animalia Filum: Chordata Kelas: Actinopterygii Ordo: Istiophoriformes Famili: Istiophoridae Genus: Istiophorus Spesies: I. platypterus Nama binomial Istiophorus platypterus(Shaw, 1792) Sinonim[2] Xiphias platypterus Shaw, 1792 Scomber gladius Bloch, 1793 Histiophorus gladius (Bloch, 1793) Istiophorus gladius (Bloch, 1793) Xiphias velifer Bloch & Schneider, 1801 Istiophorus gladif...

Matrix-assisted laser desorption electrospray ionization (MALDESI) was first introduced in 2006 as a novel ambient ionization technique which combines the benefits of electrospray ionization (ESI) and matrix-assisted laser desorption/ionization (MALDI).[1] An infrared (IR) or ultraviolet (UV) laser can be utilized in MALDESI to resonantly excite an endogenous or exogenous matrix. The term 'matrix' refers to any molecule that is present in large excess and absorbs the energy of the las...

Pour les articles homonymes, voir Coming Home. Coming Home Chanson de Sigurjón's Friends auConcours Eurovision de la chanson 2011extrait de l'album Coming Home Sortie 2011 Durée 3:01 Langue Anglais Genre Pop Auteur Þórunn Erna Clausen Compositeur Sigurjón Brink Classement 20e de la finale (61 points) Chansons représentant l'Islande au Concours Eurovision de la chanson Je ne sais quoi(2010) Never Forget(2012)modifier Coming Home (en français Rentrer à la maison) est la chanson re...

2012 compilation album by Michael FranksThe Dream 1973-2011Compilation album by Michael FranksReleased3 April 2012 (2012-04-03)Recorded1973–2011GenreJazzVocal jazzSmooth jazzLanguageEnglishLabelWarner Music FranceMichael Franks chronology Time Together(2011) The Dream 1973-2011(2012) The Music in My Head(2018) The Dream 1973-2011 is a jazz vocal boxed set album by Michael Franks, released in 2012 with Warner Music France.[1] The compilation includes 72 tracks...

Riviera del BrentaIl Naviglio del Brenta a Mira Stati Italia Regioni Veneto Superficie301,3 km² Abitanti129 598 (1-1-2017) Densità430 ab./km² I comuni costituenti la Riviera del Brenta Sito principale La Riviera del Brenta è un'area urbana della città metropolitana di Venezia che si estende lungo le rive del Naviglio del Brenta. È l'antico alveo naturale del fiume Brenta: si dirama da quest'ultimo all'altezza di Stra e, scorrendo sostanzialmente da ovest a ...

هنودمعلومات عامةنسبة التسمية الهند التعداد الكليالتعداد قرابة 1.21 مليار[1][2]تعداد الهند عام 2011ق. 1.32 مليار[3]تقديرات عام 2017ق. 30.8 مليون[4]مناطق الوجود المميزةبلد الأصل الهند البلد الهند الهند نيبال 4,000,000[5] الولايات المتحدة 3,982,398[6] الإمار...

US Open 2012Qualificazioni singolare maschileSport Tennis Tornei Singolare uomini (q) donne (q) ragazzi ragazze Doppio uomini donne misto ragazzi ragazze 2011 2013 Voci principali: US Open 2012, US Open 2012 - Singolare maschile. Le qualificazioni del singolare maschile dell'US Open 2012 sono state un torneo di tennis preliminare per accedere alla fase finale della manifestazione. I vincitori dell'ultimo turno sono entrati di diritto nel tabellone principale. In caso di ritiro di uno o...

This article does not cite any sources. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Fifth Kohl cabinet – news · newspapers · books · scholar · JSTOR (December 2009) (Learn how and when to remove this message) Fifth Cabinet of Helmut Kohl Cabinet Kohl V17th Cabinet of the Federal Republic of Germany15 November 1994 – 27 October 1998Helmut KohlDate formed15 No...

أناتول رابوبورت (بالروسية: Анато́лий Бори́сович Рапопо́рт) معلومات شخصية الميلاد 22 مايو 1911 لوزوفا الوفاة 20 يناير 2007 (95 سنة) [1] تورونتو سبب الوفاة ذات الرئة مواطنة الولايات المتحدة (1928–) الإمبراطورية الروسية عضو في الأكاديمية الأمريكية للفنون �...

British long distance runner (1938–2021) For the rugby league footballer, see Ronald Hill. Ron HillMBEHill at the Enschede Marathon in 1975Personal informationBorn(1938-09-25)25 September 1938Accrington, Lancashire, EnglandDied23 May 2021(2021-05-23) (aged 82)Hyde, Cheshire, England[1]Height1.67 m (5 ft 6 in)Weight61 kg (134 lb)SportSportLong-distance runningClubClayton-Le-Moors Harriers, LancashireAchievements and titlesOlympic finals1964, 1968, 1972 M...

Men's triple jumpat the Games of the XV OlympiadAdhemar da Silva (1956)VenueHelsinki Olympic StadiumDateJuly 23Competitors35 from 23 nationsWinning distance16.22 WRMedalists Adhemar da Silva Brazil Leonid Shcherbakov Soviet Union Asnoldo Devonish Venezuela← 19481956 →Athletics at the1952 Summer OlympicsTrack events100 mmenwomen200 mmenwomen400 mmen800 mmen1500 mmen5000 mmen10,000 mmen80 m hurdleswomen110 m hurdlesmen400 m hurdlesmen3000 msteeplec...

海洋岛海洋岛卫星照片(2008年,↑东)海洋岛海洋岛在辽宁省的位置地理位置亚洲/黄海坐标39°02.4′N 123°09.5′E / 39.0400°N 123.1583°E / 39.0400; 123.1583类型基岩岛群岛长山群岛面積18.19平方公里(7.02平方英里)海岸線33.75千米(20.971英里)最高海拔373米(1224英尺)最高點哭娘顶管轄 中华人民共和国省辽宁省市大连市县长海县镇海洋岛镇人口统计人口5,353(...
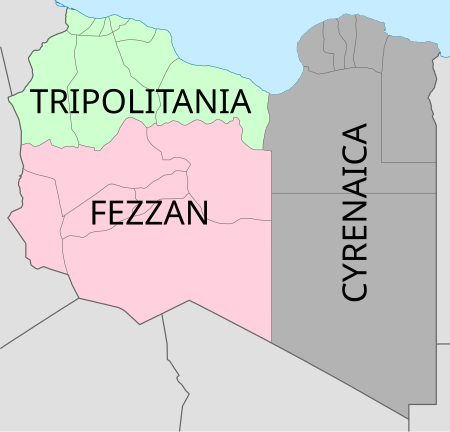
Government body in State of Libya Libya Dawn redirects here. For Operation Libya Dawn, see Battle of Tripoli Airport. Not to be confused with Government of National Salvation or Government of National Stability. This article needs editing to comply with Wikipedia's Manual of Style. Please help improve the content. (November 2015) (Learn how and when to remove this message) National Salvation Governmentحكومة الإنقاذ الوطنيProvisional Government overviewFormed6 September 20141...

Part of a series onForced labour and slavery Contemporary Child Labour Child soldiers Conscription Debt Forced marriage Bride buying Child marriage Wife selling Forced prostitution Human trafficking Peonage Penal labour Contemporary Africa 21st-century jihadism Sexual slavery Wage slavery Historical Antiquity Egypt Babylonia Greece Rome Medieval Europe Ancillae Black Sea slave trade Byzantine Empire Kholop Prague slave trade Serfs History In Russia Emancipation Thrall Genoese slave trade Ven...

彭定康勳爵閣下The Rt Hon. The Lord Patten of Barnes2019年的彭定康 欧洲联盟執委會外交專員任期1999年9月16日—2004年11月22日主席羅馬諾·普羅迪若澤·曼努埃爾·巴羅佐前任莱昂布里坦(英语:Leon Brittan)继任贝尼塔·费雷罗 - 瓦尔德纳(英语:Benita Ferrero-Waldner) 英屬香港第28任總督任期1992年7月9日—1997年6月30日君主伊利沙伯二世布政司霍德爵士陳方安生前任衛奕信勳爵继�...
Theories about the end of the universe End of the universe redirects here. For the physical location, see Shape of the universe. For the TV series episode, see End of the Universe (LEXX episode). For religious conceptions, see Eschatology. This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Ultimate fate of the universe – news · ...

Omicidio di adolescenti israeliani del 2014strageData12 giugno 2014 LuogoGush Etzion, Cisgiordania Stato Israele Coordinate31°39′16.98″N 35°07′20.22″E31°39′16.98″N, 35°07′20.22″E ResponsabiliSospetti: due militanti di Hamas da Hebron ConseguenzeMorti3 adolescenti Modifica dati su Wikidata · Manuale Il 12 giugno 2014, 3 adolescenti israeliani furono rapiti alla fermata dell'autobus presso l'insediamento israeliano di Alon Shvut a Gush Etzion, in Cisgiordania, men...

دولة فيتنام 1949–1955 دولة فيتنامشعار عاصمة مدينة هو تشي منه نظام الحكم غير محدّد نظام الحكم دولة مرتبطة التاريخ التأسيس 2 يوليو 1949 النهاية 26 أكتوبر 1955 المساحة المساحة 173809 كيلومتر مربع السكان السكان 12000000 تعديل مصدري - تعديل دولة فيتنام (بالإنجليزية...






























