ń┤ĀµĢ░ŃüīńäĪµĢ░Ńü½ÕŁśÕ£©ŃüÖŃéŗŃüōŃü©Ńü«Ķ©╝µśÄ
|
Read other articles:

Lukisan Sukadewa dirayu bidadari Ramba, karya Raja Ravi Varma (1894). Sukadewa (Dewanagari: ÓżČÓźüÓżĢÓż”ÓźćÓżĄ; ,IAST: ┼Üukadeva, ÓżČÓźüÓżĢÓż”ÓźćÓżĄ) atau Suka (Dewanagari: ÓżČÓźüÓżĢ; ,IAST: ┼Üuka, ÓżČÓźüÓżĢ) adalah nama seorang resi (petapa suci) dalam kepercayaan Hindu. Menurut pustaka suci Hindu, ia merupakan putra Resi Byasa, dan menjadi narator bagi kitab Bhagawatapurana. Sebagian besar isi naskah Bhagawatapurana terdiri dari kisah-kisah yang dituturkan Sukadewa kepad...
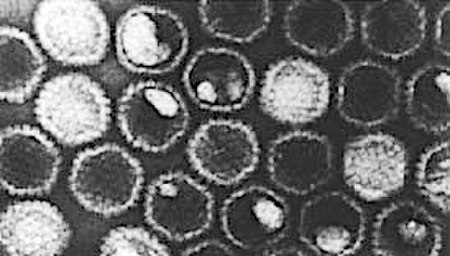
Genus of viruses Iltovirus Transmission electron micrograph of Gallid alphaherpesvirus 1 virions Virus classification (unranked): Virus Realm: Duplodnaviria Kingdom: Heunggongvirae Phylum: Peploviricota Class: Herviviricetes Order: Herpesvirales Family: Orthoherpesviridae Subfamily: Alphaherpesvirinae Genus: Iltovirus Species See text Iltovirus is a genus of viruses in the order Herpesvirales, in the family Herpesviridae, in the subfamily Alphaherpesvirinae. Birds, galliform birds, psittacine...

Protected area in New South Wales, AustraliaBrunswick Heads Nature ReserveNew South WalesIUCN category IV (habitat/species management area) Littoral rainforest in the reserveBrunswick Heads Nature ReserveNearest town or cityBrunswick HeadsCoordinates28┬░32.133ŌĆ▓S 153┬░33.206ŌĆ▓E / 28.535550┬░S 153.553433┬░E / -28.535550; 153.553433EstablishedJanuary 1979 (1979-01)Area2.21 km2 (0.9 sq mi)[1]Managing authoritiesNSW National Parks & ...

His ExcellencyLazarus ChakweraLazarus Chakwera saat pidato pelantikannya Presiden Malawi ke-6PetahanaMulai menjabat 28 Juni 2020Wakil PresidenSaulos Chilima PendahuluPeter MutharikaPenggantiPetahanaMenteri PertahananPetahanaMulai menjabat 28 Juni 2020WakilJean Munaowauza Sendeza PendahuluPeter MutharikaPenggantiPetahana Informasi pribadiLahirLazarus McCarthy Chakwera5 April 1955 (umur 69)[1]Lilongwe, Federasi Rhodesia dan Nyasaland (sekarang Malawi)Partai politikPartai Ko...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Casablanca Fan Company ŌĆō news ┬Ę newspapers ┬Ę books ┬Ę scholar ┬Ę JSTOR (August 2019) (Learn how and when to remove this message) Casablanca Fan CompanyTraded asNYSE: CABFounded1974; 50 years ago (1974)[1]FounderBurton A. BurtonFatePurcha...

Species of bird Philippine honey buzzard Conservation status Least Concern (IUCN 3.1)[1] Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Chordata Class: Aves Order: Accipitriformes Family: Accipitridae Genus: Pernis Species: P. steerei Binomial name Pernis steereiWL Sclater, 1919 Subspecies[2] P. s. winkleri - Gamauf & Preleuthner, 1998 P. s. steerei - Sclater, WL, 1919 Synonyms Pernis celebensis winkleri Gamauf & Preleuthner, 1998 The ...

British diplomat Sir Ivor RobertsKCMG FCILSir Ivor in London, November 2011British Ambassador to ItalyIn office2003ŌĆō2006MonarchElizabeth IIPrime MinisterTony BlairPreceded byJohn ShepherdSucceeded byEdward ChaplinBritish Ambassador to IrelandIn office1999ŌĆō2003MonarchElizabeth IIPrime MinisterTony BlairPreceded byVeronica SutherlandSucceeded byStewart EldonBritish Ambassador to YugoslaviaIn office1994ŌĆō1997MonarchElizabeth IIPrime MinisterJohn MajorPreceded byNew MissionSucceeded byBr...

La citt├Ā dei mostriUna scena del filmTitolo originaleThe Haunted Palace Lingua originaleinglese Paese di produzioneStati Uniti d'America Anno1963 Durata87 min Rapporto2,35:1 Genereorrore RegiaRoger Corman SoggettoHoward Phillips Lovecraft SceneggiaturaCharles Beaumont, Francis Ford Coppola (non accreditato) ProduttoreRoger Corman Produttore esecutivoSamuel Z. Arkoff, James H. Nicholson, Ronald Sinclair FotografiaFloyd Crosby MontaggioRonald Sinclair MusicheRonald Stein ScenografiaDaniel Hall...

This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) The topic of this article may not meet Wikipedia's general notability guideline. Please help to demonstrate the notability of the topic by citing reliable secondary sources that are independent of the topic and provide significant coverage of it beyond a mere trivial mention. If notability cannot be shown, the article is likely to be merged,...

Location of Djibouti This is a list of butterflies of Djibouti. About nine species are known from Djibouti,[1] none of which are endemic.[2] Pieridae Pierinae Colotis danae eupompe (Klug, 1829) Colotis halimede (Klug, 1829) Lycaenidae Theclinae Theclini Iolaus tajoraca Walker, 1870 Deudorix livia (Klug, 1834) Polyommatinae Polyommatini Tarucus rosacea (Austaut, 1885) Nymphalidae Satyrinae Satyrini Ypthima asterope (Klug, 1832) Nymphalinae Nymphalini Hypolimnas bolina jacintha...

Icelandic doctor This is an Icelandic name. The last name is patronymic, not a family name; this person is referred to by the given name ├×├│r├│lfur. ├×├│r├│lfur Gu├░nasonBorn (1953-10-28) 28 October 1953 (age 70)IcelandNationalityIcelandicEducationUniversity of Iceland 1981University of Connecticut 1988University of Minnesota 1990Medical careerFieldInfectious Disease Control ├×├│r├│lfur Gu├░nason (born 28 October 1953) is an Icelandic doctor who serverd as the Chief Epidemiologist of th...

Hindu temple in Kerala, India Sri Thrikkuratty Mahadevan | Sheeveli Thidambu | Mannar Thrikkuratty Mahadeva Temple. Mannar Thrikkuratti Mahadeva TempleMain Temple StructureReligionAffiliationHinduismDistrictAlappuzhaDeityShiva, KrishnaFestivalsMaha ShivaratriLocationLocationMannar, ParumalaStateKeralaCountry IndiaThrikkuratti Mahadeva Temple, Mannar, Alappuzha, KeralaGeographic coordinates9┬░19ŌĆ▓11ŌĆ│N 76┬░32ŌĆ▓01ŌĆ│E / 9.3195895┬░N 76.5337397┬░E / 9.3195895; 76....

Paraphyletic group of autotrophic eukaryotes in the clade Archaeplastida For an explanation of its other names, see Viridiplantae and Plantae. For the bacteria commonly known as blue-green algae that can produce toxic blooms in lakes and other waters, see Cyanobacteria. Green algae Stigeoclonium, a chlorophyte green alga genus Scientific classification (unranked): Archaeplastida Kingdom: Plantae Groups included Mesostigmatophyceae Spirotaenia Chlorokybophyceae Chlorophyta Charophyta Cladistic...

Combat aux vaisseaux devant Troie.Sarcophage n├®o-attique du Mus├®e arch├®ologique de Thessalonique, deuxi├©me quart du IIIe si├©cle apr. J.-C. La guerre de Troie est un conflit l├®gendaire de la mythologie grecque, dont l'historicit├® est controvers├®e. C'est le prince troyen P├óris qui la d├®clenche en enlevant H├®l├©ne, ├®pouse du roi de Sparte, M├®n├®las. En r├®torsion, M├®n├®las, l'├®poux bafou├®, l├©ve avec son fr├©re Agamemnon une exp├®dition rassemblant la plupart des rois grecs...

ž▒┘łž©ž▒ž¬ ┘łž¦ž▒┘Ŗ┘åž¼ž¬┘ł┘å ┘ģž╣┘ä┘ł┘ģž¦ž¬ ž┤ž«žĄ┘Ŗž® ž¦┘ä┘ģ┘Ŗ┘䞦ž» 22 žŻž║ž│žĘž│ 1838 ž¬ž¦ž▒┘Ŗž« ž¦┘ä┘ł┘üž¦ž® 20 ┘ģž¦ž▒ž│ 1907 (68 ž│┘åž®) ┘ģ┘łž¦žĘ┘åž® ž¦┘ä┘ģ┘ģ┘ä┘āž® ž¦┘ä┘ģž¬žŁž»ž® ┘äž©ž▒┘ŖžĘž¦┘å┘Ŗž¦ ž¦┘äž╣žĖ┘ģ┘ē ┘łžŻ┘Ŗž▒┘ä┘åž»ž¦ ž╣žČ┘ł ┘ü┘Ŗ ž¦┘äž¼┘ģž╣┘Ŗž® ž¦┘ä┘ģ┘ä┘ā┘Ŗž® ž¦┘䞣┘Ŗž¦ž® ž¦┘äž╣┘ģ┘ä┘Ŗž® ž¦┘ä┘ģ┘ć┘åž® ┘ā┘Ŗ┘ģ┘Ŗž¦ž”┘Ŗžī ┘ł┘ā┘Ŗ┘ģ┘Ŗž¦ž”┘Ŗ ž▓ž▒ž¦ž╣┘Ŗ ž¦┘ä┘äž║ž¦ž¬ ž¦┘äžź┘åž¼┘ä┘Ŗž▓┘Ŗž® ┘ģ┘łžĖ┘ü ┘ü┘Ŗ ž¼ž¦┘ģž╣ž® žŻ┘āž│┘ü┘łž▒ž» ž¬ž╣ž»┘Ŗ’┐Į...

Wang Jinpyng Wang Jin-pyng (Hanzi: ńÄŗķćæÕ╣│, hanyu pinyin: W├Īng J─½np├Łng; lahir 17 Maret 1941) adalah seorang negarawan Taiwan/Republik Tiongkok. Ia adalah ketua parlemen yang sekarang, juga pernah menjabat sebagai wakil ketua Kuomintang. Sebagai salah satu tokoh utama Kuomintang, Wang dianggap lembut dan suka mendamaikan. Didahului oleh:Liu Sung-pan Presiden Yuan Legislatif1999-kini Diteruskan oleh:masih menjabat Pengawasan otoritas Umum VIAF 1 2 WorldCat (via VIAF) Perpustakaan nasi...
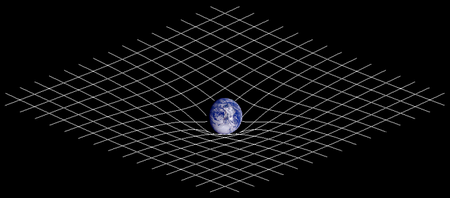
Relativitas khusus Prinsip relativitas Teori relativitas Relativitas khusus ganda Relativitas khusus invarian de Sitter Relativitas umum Dasar Simultanitas Relativitas simultanitas Gerakan relatif Kerangka acuan Kerangka acuan inersia Kerangka diam Kerangka pusat momentum Laju cahaya Persamaan Maxwell Transformasi Lorentz Konsekuensi Dilasi waktu Dilasi waktu gravitasi Massa relativistik Ekuivalensi massaŌĆōenergi Kontraksi panjang Relativitas simultanitas Efek Doppler relativistik Presesi Th...

French footballer Jules Vandooren Jules Vandooren (right), 1939Personal informationDate of birth 30 December 1908Place of birth Armenti├©res, FranceDate of death 7 January 1985(1985-01-07) (aged 76)Place of death Calais, FrancePosition(s) DefenderYouth career US P├®renchies JA Armenti├©resSenior career*Years Team Apps (Gls)1927ŌĆō1940 Olympique Lillois 1940ŌĆō1941 Red Star 1941ŌĆō1943 Reims[1] International career1933ŌĆō1942 France 22 (0)Managerial career1941ŌĆō1943 Reims1943ŌĆō1...

ąŻ čŹč鹊ą│ąŠ č鹊ą┐ąŠąĮąĖą╝ą░ ąĄčüčéčī ąĖ ą┤čĆčāą│ąĖąĄ ąĘąĮą░č湥ąĮąĖčÅ, čüą╝. ąĀą░ąĘčŖąĄąĘąČą░čÅ čāą╗ąĖčåą░. ąĀą░ąĘčŖąĄąĘąČą░čÅ čāą╗ąĖčåą░ ą×ą▒čēą░čÅ ąĖąĮč乊čĆą╝ą░čåąĖčÅ ąĪčéčĆą░ąĮą░ ąĀąŠčüčüąĖčÅ ąōąŠčĆąŠą┤ ąĪą░ąĮą║čé-ą¤ąĄč鹥čĆą▒čāčĆą│ ąĀą░ą╣ąŠąĮ ą”ąĄąĮčéčĆą░ą╗čīąĮčŗą╣ ą¤čĆąŠčéčÅąČčæąĮąĮąŠčüčéčī 890 ą╝ ą£ąĄčéčĆąŠ ąÆą╗ą░ą┤ąĖą╝ąĖčĆčüą║ą░čÅ/ ąöąŠčüč鹊ąĄą▓čüą║ą░čÅ ąøąĖą│ąŠą▓čüą║ąĖą╣ ą┐čĆąŠčüą┐ąĄą║čé ą¤čĆąĄąČąĮąĖąĄ ąĮą░ąĘą▓ą░ąĮąĖčÅ ąĀą░ąĘčŖąĄąČąČą░čÅ čāą╗ąĖčåą░,ąĀą░ąĘčŖąĄąČą░...

NGC 500 La galaxie lenticulaire NGC 500 Donn├®es dŌĆÖobservation(├ēpoque J2000.0) Constellation Poissons Ascension droite (╬▒) 01h 22m 39,4s[1] D├®clinaison (╬┤) 33┬░ 27′ 38″ [1] Magnitude apparente (V) 14,2 [2] 15,2 dans la Bande B[2] Brillance de surface 13,40 mag/am2[2] Dimensions apparentes (V) 0,8ŌĆ▓ ├Ś 0,6ŌĆ▓ [2] D├®calage vers le rouge +0,041072 ┬▒ 0,000113 [1] Angle de position 102┬░ [2] Localisation dans la constellation : Poissons Astrom├®t...












