浜学園

画像提供依頼：本部外観の画像提供をお願いします。（2024年12月）
株式会社浜学園
種類 株式会社
市場情報 非上場
略称 浜
本社所在地 日本の旗 日本
〒662-0832
兵庫県西宮市甲風園1丁目5-24
設立 1959年
業種 教育、学習支援
法人番号 9140001069970 ウィキデータを編集
事業内容 学習塾の展開、通信教育、出版など
代表者 代表取締役社長　竹森勝俊
資本金 5億5000万円（グループ計）
売上高 110億円（2020年6月期・グループ計）
従業員数 1480名
関係する人物 理事長　竹森勝昭
副理事長　橋本憲一
学園長　松本茂
副学園長　川畑清之
副学園長　加藤博規
副学園長　小澤博則
外部リンク https://www.hamagakuen.co.jp/
テンプレートを表示

株式会社浜学園（はまがくえん）は、兵庫県西宮市に本部を置く進学塾。主な業務は小学生を対象とした中学受験学習指導。

概要

主力事業である学習塾から、通信教育、出版事業などを手掛ける日本の企業である。学習塾として中学受験指導を行う進学教室浜学園は、塾生数約8000名を擁する主力事業。シンボルカラーは黄色で、標語として常在戦場を掲げている。通信教育としてeラーニングを利用した浜学園Webスクールを提供しており、出版事業として小学館と協力し有名中学合格事典を発売。その他、個別指導を行う「Hamax」、幼児教室「はまキッズ」、自学自習プログラム「はま道場」を展開するほか、小学館、小学館集英社プロダクションとテレビドラゼミの運用も行っている。理事長は竹森勝昭。副理事長は橋本憲一。学園長は松本茂。浜学園マスコットキャラクターはオルパス。

沿革

  • 1959年 - 上治貞子により兵庫県尼崎市潮江に創立。当時の名称は「英語・数学塾」。
  • 1960年 - 尼崎市・浜に教室を移転し「浜学園」と改称。当時の浜学園は上治貞子とその夫の上治義雄、そして理事長の弟の3人によって運営された。塾生は創設時2名であった。
  • 1964年 - 尼崎市・下坂部に教室移転。
  • 1972年 - 灘中に創設以来最初の合格者を出す（1名）。
  • 1973年 - 伊丹に最初の分教室を開設。第一回公開学力テストの実施。
  • 1974年 - 西宮進出。上治義雄が理事長に就任。浜学園教育基本方針や公開学力テスト・復習テストのフォーマット作成、生徒による授業アンケートの導入といった現在までに至る浜学園の根幹を創る。
  • 1978年 - 浜学園の入塾資格が得られなかった生徒を対象とした「同学社」設立。現浜学園西宮本部開設。
  • 1979年 - 高校部開設。
  • 1981年 - 灘中合格者日本一(31名)達成。
  • 1982年 - 塾生数5000名突破。
  • 1991年 - 四条烏丸教室開設に伴い京都進出。
  • 1992年 - 上治夫妻に浜学園の後継者として指名され、経営を任されていた当時の学園長前田卓郎と主力講師が、「専任講師不要論」を唱える経営陣に反発し、退職。浜学園の、受験生を含む多くの生徒を引き連れて独立し希学園を設立した。これに対し、浜学園は生徒名簿持ち出し、教材の盗用の2点で前田らを訴える事態に発展する。
  • 1993年 - 浜学園授業宣言「疲れた身に鞭打ち、時間をかけて遠方より来てくれた子供たちに応え、彼らが心から満足する授業を私たちは提供します。」制定。
  • 1995年 - 阪神・淡路大震災により多くの設備が破損。同年1993年より途絶えていた灘中合格者日本一(64名)を奪還。
  • 1996年 - 西大寺教室開設をもって奈良へ進出。
  • 2002年 - 学校週5日制に伴い、浜学園土曜スクール開講。竹森勝昭が理事長に就任。
  • 2003年 - 名古屋教室開設をもって名古屋に進出。Hamax開講。新体制の経営方針に反発した、当時の学園長宗清勝安とこれに賛同した主力級を含む講師陣がWinの母体である投資会社の支援を受け、FELIXを立ち上げ独立。これを受けて、新学園長に歴代最年少の学園長として橋本憲一（算数科）、副学園長に八幡義治（社会科）が就任。
  • 2005年 - 和歌山教室を開設し和歌山県へ進出。また岡山教室も開設され、岡山県に進出を果たす。はまキッズ開講。
  • 2006年 - 姫路教室開設。
  • 2007年 - 神戸住吉教室開設
  • 2008年- 2月に京橋教室、加古川教室開設、7月に千里中央教室と伊丹教室開設、9月に名古屋初の平日授業校千種教室開設。
  • 2009年 - NTTレゾナントとインタラクティブウェブをテーマにした「みんなでチャレンジ・全国統一難関中学模試」を発表[1]。一般コース、公開解説講義、説明会の映像化ならびに塾生向けインターネット配信を開始し、eラーニングに参入した。
  • 2010年 - 一部教室で河合塾マナビスの運営を開始。マスターコースの映像を中心とした浜学園Webスクールの開講。草津教室開設をもって滋賀県に進出。NTTラーニングシステムズ、NTTスマートコネクト、西日本電信電話、デジタルアーツ[2]、SOBAプロジェクトとの協業[3] を開始。テレビ電話システムを活用した個別指導サービスに参入。
  • 2011年 - YouTubeのコンテンツパートナーとなり、パートナーチャンネルを開設[4]。NTTぷららのひかりTVを活用したEラーニング環境トライアル。日本電信電話、西日本電信電話とのAndroidタブレットを活用した共同研究[5]、日立ソリューションズとの電子黒板を活用したデジタル教材の共同研究[6] を発表。JR京都駅前教室、神戸元町教室開設。
  • 2012年 - 2月小学館とデジタルコンテンツの共同研究[7] を発表。11月小学館、西日本電信電話、NTTラーニングシステムズとの4社協業とテレビドラゼミ、浜学園シラベテを発表[8]。泉大津、堺東の両教室開講。また12月27日名古屋市にいりなか教室を開講[9]。
  • 2013年 - 2月浜学園シラベテ正式サービス開始、4月テレビドラゼミ開講。小学館の学習漫画の一部を監修開始、9月小学館と協力し有名中学合格事典発売。10月駿台予備学校と合弁で「駿台浜学園」設立、お茶の水教室開講。
  • 2014年 - 2月NTTスマートコネクト、西日本電信電話、NTTラーニングシステムズとの4社協業による光Webスクールを発表[10]。8月NTTラーニングシステムズと浜学園シラベテへの画像認識機能追加を発表。愛知県高校受験専門「浜進学会」設立。「台湾浜学園」設立(海外に進出)、大阪府小学校受験対応「はまキッズ小学校受験コース」開始
  • 2015年 - 進学会と合弁で「浜進学会」を設立、3月に金山駅前校を開設。
  • 2018年 - 11月に浜学園円町教室開校。翌年2月から授業を開始する。
  • 2019年 - 60周年を迎え、塾生にオリジナルノートと本のしおり、リングファイルをプレゼントする。通算31回目の灘中合格者数日本一で初の100名突破(102名)。
  • 2020年 - 12月に一宮教室開設。
  • 2021年 - 2月に那覇教室開設をもって沖縄県に進出。
  • 2022年 - 2月に刈谷教室開設。4月に橋本憲一学園長が副理事長に、八幡義治副学園長が常務理事に就任。後任の新学園長に松本茂（社会科）が、新副学園長に小澤博則（算数科）、川畑清之（国語科）、加藤博規（理科）の3名が就任する新体制が発足。
  • 2023年 - 2月に奈良県４教室目となる奈良学園前教室開設。また、日能研西宮教室本部を買収し、西宮教室(5号館)とした。

教室一覧

  • 兵庫県
    • 西宮本部
    • 西神中央本部
    • 三田本部
    • 明石本部
    • 伊丹教室
    • 六甲教室
    • 神戸元町教室
    • 川西教室
    • 宝塚教室
    • 神戸住吉教室
    • 姫路教室
    • 加古川教室
    • 芦屋教室
  • 大阪府
    • 上本町本部
    • 天王寺本部
    • 豊中本部　　　　　　　
    • 枚方本部
    • なかもず本部　　　　
    • 茨木教室
    • 天六教室
    • 京橋教室
    • 千里中央本部
    • いずみ教室
    • 堺東教室
    • 泉大津教室
    • 高槻教室
  • 愛知県
    • 名古屋本部
    • 千種教室
    • 八事教室
    • 御器所教室
    • 藤が丘教室
    • 豊田教室
    • 一宮教室
    • 刈谷教室
    • 浜進学会 金山駅前校
    • 浜進学会 八事滝川校
  • 神奈川県
    • 駿台浜学園　センター南教室
    • 駿台浜学園　横浜教室
  • 東京都
    • 駿台浜学園　お茶の水教室
    • 駿台浜学園　吉祥寺教室
    • 駿台浜学園　成城教室
    • 駿台浜学園　自由が丘教室
    • 駿台浜学園　豊洲教室
  • 国外
    • 台湾浜学園

学習システム

マスターコース　塾生必修。

土曜マスターコース　土曜日に1週間分の授業をこの日1日で実施する。

Web マスターコース　マスターコースや土曜マスターコースのように塾に行かずに家でWebを見て勉強する方法。マスターコース・土曜マスターコースと選択可能。

最高レベル特訓算数　小学1年生～小学6年生

最高レベル特訓国語　小学5年生～小学6年生

最高レベル特訓理科　小学6年生

最難関レベル特訓算数　小学6年生（2月～7月）

最難関レベル特訓国語　小学6年生（2月～7月）

神女算数特訓　小学6年生（2月～7月）

日曜錬成特訓　小学6年生（2月～6月）

日曜志望校別特訓　小学6年生（7月～12月）

入試直前特訓　小学6年生（12月～1月）

灘中合格特訓　小学1年生～小学6年生

不祥事

著作権侵害問題

  • 同学園が、学園が使用する小学校の社会科用テキストについて、出版社の許諾を得ないままコピーしたものを、少なくとも約10年以上にわたり使用していたことが、2012年になって発覚した。同学園は謝罪し、今はそのテキストは使用されていない。

教え子に対する猥褻事件

  • 2013年8月21日、大阪府警は茨木教室に勤務していた、28歳男性講師を強制わいせつ罪で逮捕した（起訴後懲戒解雇）と発表した。この講師は“ご褒美”と称して教え子の小学生女子児童（事件後に退塾）の体を触っていた。「褒美」として児童らにキャラクター入りの文房具をプレゼントしており、人気講師の一人だったというが、わいせつ行為をした後にも文房具をあげていたという。

脚注

[脚注の使い方]
  1. ^ http://help.goo.ne.jp/info/detail/1336/
  2. ^ http://www.daj.jp/company/release/2010/r111501.htm
  3. ^ http://www.soba-project.com/03_press/for_media/pdf/hamagakuen_web_private_lesson.pdf
  4. ^ http://www.youtube.com/user/HamagakuenWeb
  5. ^ http://www.ntt-west.co.jp/news/1109/110922b.html
  6. ^ http://www.hitachi-solutions.co.jp/company/press/news/2011/1125.html
  7. ^ http://resemom.jp/article/2012/02/07/6183.html
  8. ^ http://www.ntt-west.co.jp/news/1211/121127a.html
  9. ^ 元名古屋セミナーの教室で、翌年2月末から浜学園の教室として使用。その後、同社の代表に浜学園の専務取締役が就くなどし、実質的に合併。
  10. ^ http://www.ntt-west.co.jp/news/1402/140226a.html

関連項目

外部リンク

ウィキメディア・コモンズには、浜学園に関連するカテゴリがあります。

Read other articles:

Burnt (film)

BurntTeaser posterSutradaraJohn WellsProduser Stacey Sher Erwin Stoff John Wells SkenarioSteven KnightCeritaMichael KalesnikoPemeran Bradley Cooper Sienna Miller Omar Sy Daniel Brühl Matthew Rhys Alicia Vikander Uma Thurman Emma Thompson Penata musikRob SimonsenSinematograferAdriano GoldmanPenyuntingNick MoorePerusahaanproduksi Shiny Penny Productions 3 Arts Entertainment Battle Mountain Films DistributorThe Weinstein CompanyTanggal rilis 22 Oktober 2015 (2015-10-22) (New Yor...

 

Современные мифы

Совреме́нные ми́фы — культурные явления, обладающие мифологической природой, но зародившиеся и существующие в культуре научно-рационального общества[1]. Явление современного мифа соотносится с процессами ремифологизации как стратегией толкования мифа, как зна�...

 

Kedunghalang, Bogor Utara, Bogor

KedunghalangKelurahanNegara IndonesiaProvinsiJawa BaratKotaBogorKecamatanBogor UtaraKodepos16158Kode Kemendagri32.71.05.1003 Kode BPS3271030007 Luas192 HaJumlah penduduk20781 pendudukKepadatan92 penduduk/m2 Pemandangan di Kedunghalang pada tahun 1920-an Kedunghalang adalah salah satu kelurahan di Kecamatan Bogor Utara, Kota Bogor, Jawa Barat, Indonesia. Sebelumnya Kedunghalang merupakan kecamatan di Kabupaten Bogor yang meliputi kecamatan Bogor Utara dan Sukaraja sekarang. Pada tahun 199...

One A.M. (film 1916)

One A.M.SutradaraCharles ChaplinProduserHenry P. CaulfieldSkenarioCharles ChaplinVincent BryanMaverick TerrellPemeranCharles ChaplinSinematograferWilliam C. FosterRoland TotherohPenyuntingCharles ChaplinDistributorMutual Film CorporationTanggal rilis 07 Agustus 1916 (1916-08-07) Durasi2 Reels (jangka penuh tak diketahui)s. 34 menitNegaraAmerika SerikatBahasaFilm bisuIntertitel Inggris One A.M. One A.M. adalah sebuah film bisu Charlie Chaplin yang dibuat untuk Mutual Film pada 1916. Film ...

 

Spermatogenesis

Artikel ini membutuhkan rujukan tambahan agar kualitasnya dapat dipastikan. Mohon bantu kami mengembangkan artikel ini dengan cara menambahkan rujukan ke sumber tepercaya. Pernyataan tak bersumber bisa saja dipertentangkan dan dihapus.Cari sumber: Spermatogenesis – berita · surat kabar · buku · cendekiawan · JSTOR artikel ini perlu dirapikan agar memenuhi standar Wikipedia. Tidak ada alasan yang diberikan. Silakan kembangkan artikel ini semampu Anda. M...

 

القوائم الحزبية للانتخابات التشريعية الإسرائيلية 2021

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (يونيو 2021) القوائم الحزبية للانتخابات التشريعية الإسرائيلية 2021معلومات عامةجزء من الانتخابات التشريعية الإسرائيلية 2021 جانب من جوانب list of Israeli politicians (en) البلد إسرائيل ب...

Ernst Brenner

Ernst Brenner Presiden Konfederasi Swiss Ke-53Masa jabatan1 Januari 1901 – 31 Desember 1901PendahuluWalter HauserPenggantiJosef ZempPresiden Konfederasi Swiss Ke-60Masa jabatan1 Januari 1908 – 31 Desember 1908PendahuluEduard MüllerPenggantiAdolf DeucherAnggota Dewan Federal SwissMasa jabatan25 Maret 1897 – 11 Maret 1911PendahuluEmil FreyPenggantiArthur Hoffmann Informasi pribadiLahir(1856-12-09)9 Desember 1856Meninggal11 Maret 1911(1911-03-11) (umur 54)K...

 

List of top-division football clubs in CONMEBOL countries

  CONMEBOL countries on this map of the world's six football confederations The South American Football Confederation (CONMEBOL) is the administrative and controlling body for association football in most of South America. It consists of 10 member associations, each of which is responsible for governing football in their respective countries.[1] It includes all countries and territories within South America, with the exceptions of Guyana, French Guiana, Suriname, which are ...

 

English Renaissance

Cultural and artistic movement in England dating from the mid-16th century to the early 17th century RenaissanceThe School of Athens (1509–1511) by Raphael Aspects Architecture Dance Fine arts Greek scholars Humanism Literature Magic Music Philosophy Science Technology Warfare Regions England France Germany Italy Poland Portugal Spain Scotland Northern Europe Low Countries History and study Age of Discovery Continuity thesis High Renaissance vte The First Appearance of William Shakespeare o...

Flag of Pembrokeshire

Flag of a Welsh county PembrokeshireProportion3:5Adopted1988DesignAzure a cross Or on an inescutcheon of five Vert a Tudor Rose quarterly counter-changed Argent and Gules.Designed byPeter Stock, Dewi Pritchard, Jim Brock and Marjorie Jacobs The flag of Pembrokeshire (Welsh: Baner Sir Benfro) is the flag of the Welsh county of Pembrokeshire. The flag was designed by Councillors Peter Stock, Dewi Pritchard, Jim Brock and Marjorie Jacobs in the 1970s after the abolition of Pembrokeshire Cou...

 

Commodore Barry Park

Public park in Brooklyn, New York Playing field Commodore Barry Park is an urban park in the Fort Greene neighborhood of the New York City borough of Brooklyn. The park is operated by the New York City Department of Parks and Recreation. It encompasses an area of 10.39 acres (42,000 m2) and holds baseball, basketball, football, swimming pool and playground fields/facilities.[1] The park was acquired in 1836 by the Village of Brooklyn (long before it was absorbed into New York Cit...

 

大字 (数字)

この項目には、一部のコンピュータや閲覧ソフトで表示できない文字が含まれています（詳細）。 数字の大字（だいじ）は、漢数字の一種。通常用いる単純な字形の漢数字（小字）の代わりに同じ音の別の漢字を用いるものである。 概要 壱万円日本銀行券（「壱」が大字） 弐千円日本銀行券（「弐」が大字） 漢数字には「一」「二」「三」と続く小字と、「壱」「�...

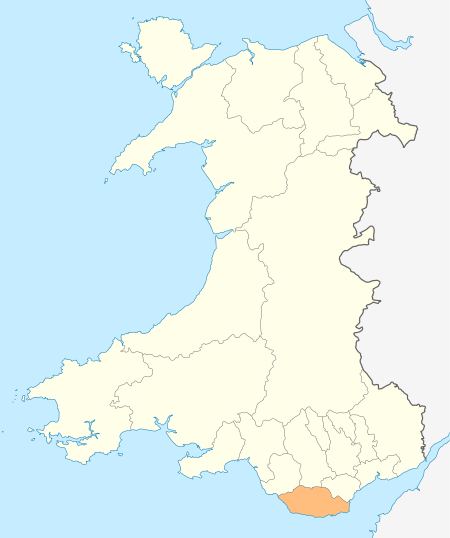
Welsh St Donats

Not to be confused with St Donats. Human settlement in WalesWelsh St DonatsWelsh: LlanddunwydSt Donat's (St Dunwyd's) churchWelsh St DonatsLocation within the Vale of GlamorganPopulation534 Principal areaVale of GlamorganPreserved countySouth GlamorganCountryWalesSovereign stateUnited KingdomPost townCowbridgePostcode districtCF71Dialling code01446PoliceSouth WalesFireSouth WalesAmbulanceWelsh UK ParliamentVale of GlamorganSenedd Cymru – Welsh ParliamentVa...

 

中华人民共和国国家元首列表

  提示：此条目页的主题不是中華人民共和國最高領導人。 中华人民共和国 中华人民共和国政府与政治系列条目 执政党 中国共产党 党章、党旗党徽 主要负责人、领导核心 领导集体、民主集中制 意识形态、组织 以习近平同志为核心的党中央 两个维护、两个确立 全国代表大会 （二十大） 中央委员会 （二十届） 总书记：习近平 中央政治局 常务委员会 中央书记处 �...

 

Massimo Ciancimino

Massimo Ciancimino, dicembre 2010 Massimo Ciancimino (Palermo, 16 febbraio 1963) è un imprenditore italiano. Pregiudicato, agli arresti domiciliari[1], teste in vari processi di mafia, a sua volta egli stesso indagato per calunnia, concorso in associazione mafiosa, condannato in via definitiva per riciclaggio di denaro e per detenzione di esplosivi Indice 1 Biografia 1.1 Il mistero del papello 1.2 Presunte minacce e intimidazioni 1.3 Testimonianze contro Berlusconi e Dell'Utri 1.4 Ac...

Johann Joachim Quantz

Johann Joachim Quantz (1697-1773), Ia adalah seorang komposer Jerman yang mempunyai peran penting dalam sebuah risalah penting suling dan membuat perbaikan mekanik di insturmen, yang menemukan kunci kedua pada seruling Johann Joachim Quantz (lahir, 30 Januari 1697 di Oberscheden, dekat Gottingen, Jerman - meninggal, 12 Juli 1773 di Potsdam, Brandenburg) adalah seorang komposer Jerman yang mempunyai peran dalam sebuah risalah penting suling dan yang membuat perbaikan mekanik di instrumen, yang...

 

بيليفيو (نبراسكا)

  لمعانٍ أخرى، طالع بيليفيو (توضيح). بيليفيو   الاسم الرسمي (بالإنجليزية: Bellevue)‏    الإحداثيات 41°09′31″N 95°56′03″W / 41.158611111111°N 95.934166666667°W / 41.158611111111; -95.934166666667   [1] تاريخ التأسيس 1822  تقسيم إداري  البلد الولايات المتحدة[2][3]  التقسيم ا�...

 

Allocative efficiency

When production relates to consumer preferences in an economy Allocative efficiency is a state of the economy in which production is aligned with the preferences of consumers and producers; in particular, the set of outputs is chosen so as to maximize the social welfare of society.[1] This is achieved if every produced good or service has a marginal benefit equal to the marginal cost of production. Description In economics, allocative efficiency entails production at the point on the ...

Multibrot set

Multibrot 3 at the bottom-left of the main part. detail of multiJulia 8. Multibrot_4. Construct in mathematics Multibrot exponent 0 - 8 In mathematics, a Multibrot set is the set of values in the complex plane whose absolute value remains below some finite value throughout iterations by a member of the general monic univariate polynomial family of recursions.[1][2][3] The name is a portmanteau of multiple and Mandelbrot set. The same can be applied to the Julia set, th...

 

Клязьма

У этого термина существуют и другие значения, см. Клязьма (значения).Клязьма Река Клязьма в черте Ногинска Характеристика Длина 686 км Бассейн 42 500 км² Расход воды 145 м³/с (у г. Коврова) Водоток Исток   (Т) (B)    • Местоположение Московская возвышенность, ...