µ£ēÕÉæķØ×ÕĘĪÕø×Ńé░Ńā®ŃāĢ
|
Read other articles:

American politician (born 1967) For other people named Connie Mack, see Connie Mack (disambiguation). Connie Mack IVMember of the U.S. House of Representativesfrom Florida's 14th districtIn officeJanuary 3, 2005 ŌĆō January 3, 2013Preceded byPorter GossSucceeded byTrey Radel (Redistricting)Member of the Florida House of Representativesfrom the 91st districtIn officeJanuary 3, 2001 ŌĆō October 10, 2003Preceded byDebby P. SandersonSucceeded byEllyn Bogd...

Pengusiran orang Morisco di pelabuhan D├®nia, oleh Vincente Mostre. Pada tanggal 9 April 1609, Raja Philip III dari Spanyol memerintahkan pengusiran orang Morisco. Orang Morisco adalah keturunan umat Islam yang pindah agama menjadi Kristen karena ancaman pengusiran dari Fernando dan Isabel pada tahun 1502. Dari 1609 hingga 1614, pemerintah Spanyol secara sistematis memaksa orang Morisco untuk meninggalkan negara tersebut dan pindah ke Afrika Utara. Mereka hanya diizinkan menyimpan uang dan ha...

Star Wars: The Rise of SkywalkerPoster perilisan teaterSutradaraJ. J. AbramsProduser Kathleen Kennedy J. J. Abrams Michelle Rejwan Ditulis oleh J. J. Abrams Chris Terrio BerdasarkanKarakteroleh George LucasPemeran Daisy Ridley Adam Driver John Boyega Oscar Isaac Lupita Nyong'o Domhnall Gleeson Kelly Marie Tran Joonas Suotamo Billie Lourd Naomi Ackie Richard E. Grant Keri Russell Mark Hamill Anthony Daniels Billy Dee Williams Carrie Fisher Ian McDiarmid Penata musikJohn WilliamsSinematog...

Simon PeggPegg pada bulan Juli 2013.LahirSimon John Beckingham14 Februari 1970 (umur 54)Brockworth, Gloucestershire, InggrisPendidikanMillbrook AcademyAlmamaterUniversitas BristolPekerjaanAktor, komedian, penulis, produser, penyanyi, sutradaraTahun aktif1995ŌĆōsekarangKarya terkenalSpacedShaun of the DeadHot FuzzPaulThe World's EndKekayaan bersih$10 juta (2011)[1]Suami/istriMaureen McCann (m. 2005)Anak1 Simon Pegg (lahir Simon John Beckin...

Pour les articles homonymes, voir 363e r├®giment. 363e r├®giment d'infanterie L'├®tendard et la garde du drapeau du 363e RI au c├┤t├® de celui du 369e RI am├®ricain d├®cor├® par le g├®n├®ral Lebouc, d├®cembre 1918. Cr├®ation Ao├╗t 1914 Dissolution Mars 1919 Pays France Branche Arm├®e de terre Type R├®giment d'infanterie R├┤le Infanterie Guerres Premi├©re Guerre mondiale D├®corations Croix de guerre 1914-1918 modifier Le 363e r├®giment d'infanterie (363e RI) est un r...

Administrative division in western Japan during the Edo period (1600-1871) Saiki DomainõĮÉõ╝»ĶŚ®Domain of Japan1600ŌĆō1871Saiki Castle Mon of the M┼Źri clan CapitalSaiki CastleArea ŌĆó Coordinates32┬░57ŌĆ▓36.83ŌĆ│N 131┬░53ŌĆ▓23.35ŌĆ│E / 32.9602306┬░N 131.8898194┬░E / 32.9602306; 131.8898194 Historical eraEdo periodŌĆó Established 1600ŌĆó Abolition of the han system 1871 Contained within ŌĆó ProvinceBungo Province Today part ofOita Pre...

Pour les autres articles nationaux ou selon les autres juridictions, voir Gendarmerie. Gendarmerie nationaleHistoireFondation Moyen ├ége (┬½ Mar├®chauss├®e ┬╗)[1]1791 (┬½ Gendarmerie nationale ┬╗)CadreType GendarmerieSi├©ge Issy-les-MoulineauxPays FranceOrganisationMembres FIEPForce de gendarmerie europ├®enneEffectif 155 000 personnels civils et militaires (2024)Ministres G├®rald Darmanin (Int├®rieur)S├®bastien Lecornu (Arm├®es)Directeur g├®n├®ral G├®n├®ra...

Pour les articles homonymes, voir Sands. Julian Sands Julian Sands en 2011. Donn├®es cl├®s Nom de naissance Julian Richard Morley Sands Naissance 4 janvier 1958Otley, Yorkshire de l'Ouest (Angleterre, Royaume-Uni) Nationalit├® Britannique Am├®ricaine D├®c├©s 13 janvier 2023 (├Ā 65 ans)Monts San Gabriel, Los Angeles, (Californie, ├ētats-Unis) Profession Acteur Films notables La D├®chirureChambre avec vueWarlockLe Festin nuLeaving Las VegasPour une nuit S├®ries notables Stargate SG-124 he...

Untuk kegunaan lain, lihat Peri (disambiguasi). Rusałki (1877), oleh Witold Pruszkowski Dalam mitologi Slavia, peri adalah makhluk perempuan yang diasosiasikan dengan suatu unsur alam. Peri Slavia muncul dalam berbagai bentuk dan namanya juga bermacam-macam tergantung bahasa. Peri Slavia di antaranya adalah khovanets (atau domovoi), dolia (takdir), polyovyk atau polevoi (roh padang), perelesnyk (roh rayuan), lesovyk atau leshyi (roh hutan), blud (peneglana), mara (hantu, roh kebingungan), ch...

Area VestinaPenne e il Gran Sasso Stati Italia Regioni Abruzzo Superficie634,23 km┬▓ Abitanti60 157[1] (31-12-2023) Densit├Ā94,85 ab./km┬▓ Fusi orariUTC+1 Nome abitantivestini L'area Vestina nella provincia di Pescara L'area Vestina ├© una zona geografica della provincia di Pescara che comprende molti comuni dell'entroterra pescarese a nord del fiume Pescara, e prende il nome dall'antico popolo italico dei Vestini che abitava la zona[2]. Molti...

ĶÄĵŗē┬Ęķś┐õ╗ĆķĀō-Ķź┐ķćīµ┤ø2023Õ╣┤8µ£ł’╝īķś┐õ╗ĆķĀō-Ķź┐ķćīµ┤øń®┐ĶæŚĶ╗Źµ£ŹÕć║ńö¤ (1977-07-09) 1977Õ╣┤7µ£ł9µŚź’╝ł46µŁ▓’╝ē ńŠÄÕ£ŗõĮøńŠģķćīķüöÕĘ×ÕøĮń▒Ź ńŠÄÕ£ŗÕł½ÕÉŹĶÄĵŗē┬Ęķś┐õ╗ĆķĀō’╝łSarah Ashton’╝ēĶÄĵŗē┬ĘĶź┐ķćīµ┤ø’╝łSarah Cirillo’╝ēķćæķ½«Õź│ķāÄ’╝łBlonde’╝ēĶüīõĖÜĶ©śĶĆģŃĆüµ┤╗ÕŗĢÕ«ČŃĆüµö┐µ▓╗µ┤╗ÕŗĢÕ«ČÕÆīÕĆÖķüĖõ║║ŃĆüĶ╗Źķå½µ┤╗ĶĘāµŚČµ£¤2020Õ╣┤ŌĆöķøćõĖ╗Õģ¦ĶÅ»ķüöÕĘ×Õģ▒ÕÆīķ╗©ÕĆÖķüĖõ║║’╝ł2020Õ╣┤’╝ēŃĆŖPolitical.tipsŃĆŗ’╝ł2020Õ╣┤ŌĆö’╝ēŃĆŖLGBTQÕ£ŗÕ║”ŃĆŗ’╝ł2022Õ╣┤3µ£łŌĆö2022Õ╣┤10µ£ł’╝ēńāÅÕģŗĶśŁÕ¬Æ’┐Į...

Chronologies Donn├®es cl├®s 1229 1230 1231 1232 1233 1234 1235D├®cennies :1200 1210 1220 1230 1240 1250 1260Si├©cles :XIe XIIe XIIIe XIVe XVeMill├®naires :-Ier Ier IIe IIIe Chronologies th├®matiques Religion (,) et * Croisades Science () et Sant├® et m├®decine Terrorisme Calendriers Romain Chinois Gr├®gorien Julien H├®bra├»que Hindou H├®girien Persan R├®publicain modifier Ann├®es de la sant├® et de la m├®decine ...

This article relies excessively on references to primary sources. Please improve this article by adding secondary or tertiary sources. Find sources: Art Directors Guild Award for Excellence in Production Design for a Fantasy Film ŌĆō news ┬Ę newspapers ┬Ę books ┬Ę scholar ┬Ę JSTOR (January 2018) (Learn how and when to remove this message) The Art Directors Guild Award for Excellence in Production Design for a Fantasy Film is one of the annual awards given by...

Province of Afghanistan This article is about a province of Afghanistan. For its capital city, see Herat. This article needs to be updated. Please help update this article to reflect recent events or newly available information. (July 2023) Province in AfghanistanHerat ┘ćž▒ž¦ž¬ProvinceFrom the top, Landscape of Herat Province, Great Mosque of Herat, Cheheltan-Chisht.Map of Afghanistan with Herat highlightedDetail map of Herat provinceCoordinates (Capital): 34┬░00ŌĆ▓N 62┬░00ŌĆ▓E / ...

┘ćž░┘ć ž¦┘ä┘ģ┘鞦┘äž® ž╣┘å ┘ł┘āž░┘ä┘ā ž¼ž» ┘ģžŁ┘ģž» ┘ģ┘ćž»┘Ŗ žŁž│┘å ž©žŁž▒ ž¦┘äž╣┘ä┘ł┘ģ ž¦┘äžĘž©ž¦žĘž©ž¦ž”┘Ŗ. ┘ä┘ģž╣ž¦┘å┘Ź žŻž«ž▒┘ēžī žĘž¦┘äž╣ ┘ģžŁ┘ģž» ┘ģ┘ćž»┘Ŗ žŁž│┘å ž¦┘äžĘž©ž¦žĘž©ž¦ž”┘Ŗ. žó┘Ŗž® ž¦┘ä┘ä┘ć ž¦┘äž╣žĖ┘ģ┘ēžī ┘łž¦┘äž│┘Ŗž» ž¦┘äž│┘Ŗž» ┘ģžŁ┘ģž» ┘ģ┘ćž»┘Ŗ ž©žŁž▒ ž¦┘äž╣┘ä┘ł┘ģ ž¦┘äžĘž©ž¦žĘž©ž¦ž”┘Ŗ ┘ģž╣┘ä┘ł┘ģž¦ž¬ ž┤ž«žĄ┘Ŗž® ž¦┘ä┘ģ┘Ŗ┘䞦ž» 1 ž┤┘łž¦┘ä 1155 ┘ć┘Ć┘āž▒ž©┘䞦žĪžī ž¦┘äž╣ž▒ž¦┘é ž¦┘ä┘ł┘üž¦ž® 22 ž▒ž¼ž© 1212 ┘ć┘Ćž¦┘ä┘åž¼┘üžī ž¦┘äž╣ž▒ž¦┘é ┘ģ┘łž¦žĘ┘åž® ž¦’┐Į...

Universit├® Loyola de ChicagoLe Cudahy Science Hall.HistoireFondation 1870StatutType j├®suiteNom officiel Loyola University ChicagoR├®gime linguistique anglaisFondateur Arnold J. Damen S.J.Devise Ad majorem Dei gloriamMembre de Association des universit├®s et facult├®s j├®suites (en), Black Metropolis Research Consortium (d), American Council on Education (en)Site web www.luc.eduChiffres-cl├®s├ētudiants 17 007 (2018)Effectif 3 473 (2020)Budget 750 millions de dollarsLocalisationPays...

µÅÉńż║’╝ܵŁżµØĪńø«ķĪĄńÜäõĖ╗ķóśõĖŹµś»ĶōØńö░ÕÄ┐ŃĆé Õģ│õ║ÄõĖÄŃĆīĶŚŹńö░ (ķ”ÖµĖ»)ŃĆŹµ©ÖķĪīńøĖĶ┐æµł¢ńøĖÕÉīńÜäµØĪńø«ķĪĄ’╝īĶ½ŗĶ”ŗŃĆīĶŚŹńö░ŃĆŹŃĆé ĶŚŹńö░Lam TinĶ¦ĆÕĪśÕŹĆÕ£░ÕŹĆÕØɵĀć’╝Ü22┬░18ŌĆ▓34ŌĆ│N 114┬░14ŌĆ▓10ŌĆ│E / 22.3094┬░N 114.236┬░E / 22.3094; 114.236Õ¤ÄÕĖéķ”ÖµĖ»Õ¤ÄÕĖéÕŹĆÕŖāõ╣ØķŠŹµØ▒ÕŹĆĶ¦ĆÕĪśÕŹĆķ¢ŗÕ¦ŗµ£ēõ║║Õ▒ģõĮÅÕēŹ9õĖ¢ń┤ƵŁĖÕģźõĖŁÕĤķĀśÕ£¤ÕēŹ2õĖ¢ń┤ƵŁĖÕģźķ”ÖµĖ»1898Õ╣┤ķØóń¦» ŌĆó ķÖĖÕ£░2.184Õ╣│µ¢╣Õģ¼ķćī ŌĆó ÕĖéÕŹĆ1.737Õ╣│µ¢╣Õģ¼’┐Į...

See also: Mexico City and Z├│calo The symbol of the founding of Mexico-Tenochtitlan, the central image on the Mexican flag since Mexican independence from Spain in 1821. The history of Mexico City stretches back to its founding ca. 1325 CE as the Mexica city-state of Tenochtitlan, which evolved into the senior partner of the Aztec Triple Alliance that dominated central Mexico immediately prior to the Spanish conquest of 1519ŌĆō1521. At its height, Tenochtitlan had enormous temples and palace...
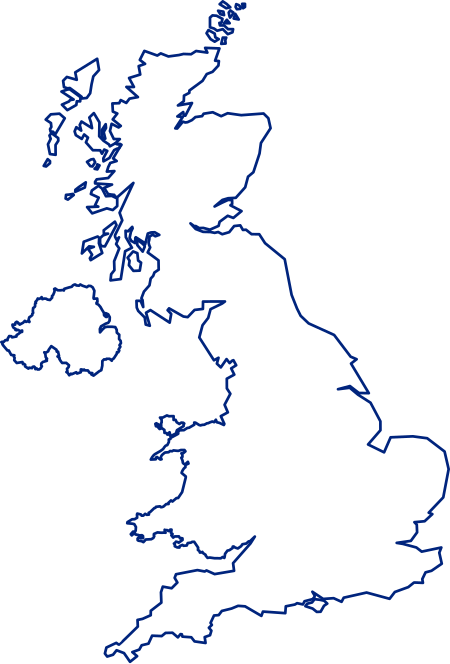
Seacroft mengarah ke sini. Anda mungkin mencari mengenai desa Seacroft, Lincolnshire. 53┬░49ŌĆ▓20ŌĆ│N 1┬░27ŌĆ▓36ŌĆ│W / 53.8222┬░N 1.4599┬░W / 53.8222; -1.4599 Seacroft Pemandangan dari Seacroft Village Green ke Cricketers Arms dan Queensview Flats dengan pusat perbelanjaan tampak di kanan. Seacroft Letak Seacroft di West Yorkshire Population 17.725 (Sensus 2001) Ref. grid OS SE362365 Distrik metropolitan Kota Leeds County metropolitan West...

Dutch politician (born 1973) This biography of a living person needs additional citations for verification. Please help by adding reliable sources. Contentious material about living persons that is unsourced or poorly sourced must be removed immediately from the article and its talk page, especially if potentially libelous.Find sources: Arjan El Fassed ŌĆō news ┬Ę newspapers ┬Ę books ┬Ę scholar ┬Ę JSTOR (April 2015) (Learn how and when to remove this message...