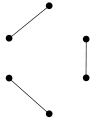
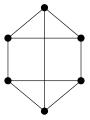
正則グラフ

正則グラフ（せいそくグラフ、英: regular graph）は、グラフ理論において、各頂点の隣接する頂点数が全て同じであるようなグラフである。すなわち、全ての頂点の次数が等しい。頂点の次数が k の正則グラフを 「k-正則グラフ」または「次数 k の正則グラフ」と呼ぶ。

次数2までの正則グラフの分類は容易である。0-正則グラフは連結されていない頂点で構成され、1-正則グラフは連結されていない辺で構成され、2-正則グラフは連結されていない閉路で構成される。

3-正則グラフは立方体グラフとも呼ばれる。

正則グラフのうち、隣接する2つの頂点に共通する隣接点が常に同じ l 個で、隣接しない2つの頂点に共通する隣接点が常に同じ n 個となっているものを強正則グラフという。正則だが強正則でない最小のグラフは、6頂点の閉路グラフかつ循環グラフである。

完全グラフ は任意の について強正則である。

クリスピン・ナッシュ＝ウィリアムズの定理によれば、2k+1 個の頂点から成る k-正則グラフには必ずハミルトン路がある。

  • 0-正則グラフ
    0-正則グラフ
  • 1-正則グラフ
    1-正則グラフ
  • 2-正則グラフ
    2-正則グラフ
  • 3-正則グラフ
    3-正則グラフ

代数的属性

あるグラフの隣接行列を A とする。そのグラフが k-正則であることは、ベクトル が固有値 k に属する A の固有ベクトルであることと同値である[1]。他の固有値に対応した固有ベクトルは と直交なので、そのような固有ベクトル について が成り立つ。

次数 k の正則グラフが連結していることと、固有値 k の重複度が1であることは同値である[1]。

正則な連結グラフの判定基準も存在する。グラフが連結かつ正則であることと、 である行列 J がそのグラフの隣接代数（Aの冪乗の1次結合）にあることは同値である。[要出典]

グラフGはk-正則グラフで、直径D、隣接行列の固有値群は とする。Gが2部グラフでないなら、次が成り立つ。

ここで である。[要出典]

生成

正則グラフを生成するソフトウェアとして GenReg がある[2]。

脚注・出典

  1. ^ a b Cvetković, D. M.; Doob, M.; and Sachs, H. Spectra of Graphs: Theory and Applications, 3rd rev. enl. ed. New York: Wiley, 1998.
  2. ^ Regular Graphs M. Meringer, J. Graph Theory, 1999, 30, 137.

関連項目

外部リンク

  • Weisstein, Eric W. "Regular Graph". mathworld.wolfram.com (英語).
  • Weisstein, Eric W. "Strongly Regular Graph". mathworld.wolfram.com (英語).
  • GenReg software and data by Markus Meringer.
  • Nash-Williams, Crispin (1969), “Valency Sequences which force graphs to have Hamiltonian Circuits”, University of Waterloo Research Report, Waterloo, Ontario: University of Waterloo 
要素・定義・表現
指標
部分構造
全体構造
固有名を持つグラフ
トピック・定理
カテゴリ カテゴリ / コモンズ コモンズ

Read other articles:

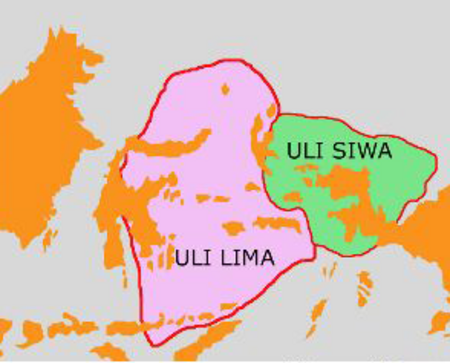
Maluku

Halaman ini berisi artikel tentang provinsi. Untuk kepulauan yang mencakup provinsi tersebut, lihat Kepulauan Maluku. Untuk kegunaan lain, lihat Maluku (disambiguasi). MalukuProvinsiDari kiri ke kanan, atas ke bawah: Bukit Desa Kaibobo, Gunung Api Banda, Tarian Cakalele, Pantai Natsepa, Pantai Yanain, dan Pantai Tanusang Geser, Pantai Ora. BenderaLambangJulukan: The Spice IslandMotto: Siwalima(Ambon) Milik bersamaPetaNegara IndonesiaDasar hukum pendirianUU RI No. 20 Tahun 1958H...

 

بوابة:شتات عربي

[تعديل]  شتات عربي مرحبًا بك يا اسم مستخدم في بوابة شتات عربي. الساعة الآن 12:55 (UTC) من يوم الثلاثاء الموافق 30 رمضان 1445 هـ عرب المهجر لفظ يدل على المهاجرين العرب، وأبنائهم ممن غادروا دولهم الأصلية بمحض إرادتهم أو كلاجئين، ويقطنون الآن في دول غير عربية، أكثرهم في أمريكا اللات...

 

Interstate 15 in California

North–south Interstate and state highway in the U.S. state of California For the original Sign Route 15, see California State Route 15 (1934-1964). This article is about the section of Interstate 15 in California. For the entire route, see Interstate 15. Interstate 15 and State Route 15I-15 highlighted in red, SR 15 in purpleRoute informationMaintained by CaltransLength295.37 mi[1][a] (475.35 km)Existed1957–presentComponenthighways SR 15 from 32nd ...

Panellenio Protathlema 1929-1930

Panellenio Protathlema 1929-1930 Competizione Panellenio Protathlema Sport Calcio Edizione 2ª Organizzatore EPO Date dal 18 maggio 1930al 29 giugno 1930 Luogo  Grecia Partecipanti 3 Risultati Vincitore Panathīnaïkos(1º titolo) Cronologia della competizione 1927-1928 1930-1931 Manuale La Panellenio Protathlema 1929-1930 è stata la seconda edizione del campionato di calcio greco la cui fase finale è stata disputata tra il 18 maggio e il 29 giugno 1930 e conclusa con la vitto...

 

Lady Hester Stanhope

Hester Stanhope Lady Hester Lucy Stanhope (12 Maret 1776 – 23 Juni 1839) adalah seorang sosialita, petualang dan penjelajah asal Inggris. Ekspedisi arkeologinya ke Ashkelon pada 1815 dianggap sebagai ekskavasi modern pertama dalam sejarah arkeologi Tanah Suci. Pemakaiannya terhadap dokumen Italia abad pertengahan disebut sebagai salah satu pemakaian terawal dari sumber-sumber tekstual oleh para arkeolog lapangan.[1][2] Catatan ^ Silberman, Neil Asher (Jul–Aug...

 

IBM 7070

Decimal computer introduced by IBM in 1958 IBM 7070Release date1958; 66 years ago (1958)Memory5,000 or 9,990 wordsPredecessorIBM 650; IBM 705SuccessorIBM System/360 IBM 7074IBM 7074Release date1960; 64 years ago (1960)Memory5,000 to 30,000 wordsPredecessorIBM 7070SuccessorIBM System/360 IBM 7072Release date1961; 63 years ago (1961)SuccessorIBM System/360 IBM 7070 is a decimal-architecture intermediate data-processing system that was introd...

أوراق الموت (مسلسل)

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (ديسمبر 2020) أوراق الموت (مسلسل) أيضاً معروف باسم Death Papers بطولة كينتو يامازاكي نيجيرو موراكامي تاو تسوتشيا البلد  اليابان لغة العمل اللغة الانجليزية عدد الحلقات 8 حلقة...

 

Congregazione dell'Annunziata

La Congregazione dell'Annunziata (in latino Congregatio ab Annuntiatione B.M.V.) è una delle congregazioni monastiche di diritto pontificio che compongono la confederazione benedettina. Indice 1 Origini 2 Missioni 3 Opere intellettuali 4 Diffusione 5 Note 6 Bibliografia Origini L'abbazia di Saint-André, una delle tre che diedero inizio alla congregazione La congregazione fu eretta da papa Benedetto XV con breve Ordo a Divo Benedicto del 20 febbraio 1920 per riunire le abbazie francofone del...

 

2022 Arizona Secretary of State election

2022 Arizona Secretary of State election ← 2018 November 8, 2022 2026 →   Nominee Adrian Fontes Mark Finchem Party Democratic Republican Popular vote 1,320,619 1,200,411 Percentage 52.38% 47.62% County results Congressional district resultsFontes:      50–60%      60–70%      70–80%Finchem:      50–60%      60–70%   &...

Google Cloud Platform

Cloud-based service and infrastructure It has been suggested that Google APIs and Google Cloud be merged into this article. (Discuss) Proposed since December 2023. This article relies excessively on references to primary sources. Please improve this article by adding secondary or tertiary sources. Find sources: Google Cloud Platform – news · newspapers · books · scholar · JSTOR (March 2022) (Learn how and when to remove this message) Google Cloud Platf...

 

Zhijiang Xinyu

Book written by Xi Jinping Zhijiang Xinyu AuthorXi JinpingCountry People's Republic of ChinaLanguageChinesePublisherZhejiang People's Publishing House[1]Publication dateAugust 2007Pages273ISBN9787213035081 Zhijiang Xinyu (Chinese: 之江新语) is a book written by Xi Jinping, then the party secretary of Zhejiang Province using the pen name Zhexin (Chinese: 哲欣). It was initially a personal column about political ideas published on the front page of Zhejiang Daily from...

 

Black's Law Dictionary

Popular American law dictionary Black's Law Dictionary Image of the 7th editionEditorBryan A. Garner(1999–present)CountryUnited StatesLanguageEnglishPublisherWest (Thomson Reuters)Publication date1891 (1st)1910 (2nd)1933 (3rd)1951 (4th)1968 (4thR)1979 (5th)1990 (6th)1999 (7th)2004 (8th)2009 (9th)2014 (10th)2019 (11th)ISBN978-1-5392-2975-9WebsiteBlack's Law Dictionary Black's Law Dictionary [BLD] is the most frequently used legal dictionary in the United States.[1] Henry Campbell...

Ghana Police Service

Main law enforcement agency of Ghana Law enforcement agency Ghana Police ServiceGhana Police Service patch depicting the service logoLogo of the Ghana Police ServiceShield of the Ghana Police ServiceCommon nameGhana Police ServiceAbbreviationGPSMottoService With IntegrityAgency overviewFormed1894Preceding agencies1894 – 1957: known as the Gold Coast Police Force1957 – known as the Ghana Police ServiceEmployees32,684 (30 June 2011)Jurisdictional structureNational agencyRepublic of Gha...

 

Landspout

Tornado not originating from a mesocyclone A landspout tornado forms from a developing thunderstorm near Cheyenne Wells, Colorado. Landspouts are exceptionally common in Eastern Colorado.[1][2] A landspout near North Platte, Nebraska, on May 22, 2004. Note the characteristic smooth, tubular shape, similar to that of a fair-weather waterspout. Landspout on September 29, 2007 Part of a series onWeather Temperate and polar seasons Winter Spring Summer Autumn Tropical seasons Dry ...

 

Kamp Koral: SpongeBob's Under Years

American animated television series Kamp Koral: SpongeBob's Under YearsAlso known asKamp KoralGenreComedyDeveloped by Luke Brookshier Marc Ceccarelli Andrew Goodman Kaz Mr. Lawrence Vincent Waller Voices of Tom Kenny Bill Fagerbakke Rodger Bumpass Clancy Brown Carolyn Lawrence Mr. Lawrence Mary Jo Catlett Jill Talley Lori Alan Carlos Alazraqui Kate Higgins Dee Bradley Baker Theme music composer Luke Brookshier Marc Ceccarelli Andrew Goodman Kaz Mr. Lawrence Eban Schletter Vincent Waller Compo...

1853 California gubernatorial election

1853 California gubernatorial election ← 1851 September 7, 1853 1855 →   Nominee John Bigler William Waldo Party Democratic Whig Popular vote 38,940 37,454 Percentage 50.97% 49.03% Governor before election John Bigler Democratic Elected Governor John Bigler Democratic Elections in California Federal government U.S. President 1852 1856 1860 1864 1868 1872 1876 1880 1884 1888 1892 1896 1900 1904 1908 1912 1916 1920 1924 1928 1932 1936 1940 1944 1948 1952 1956 19...

 

Economy of the Habsburg monarchy

This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (September 2017) (Learn how and when to remove this message) Habsburg monarchy in 1789 Golden ducat of Ferdinand I, minted in Klagenfurt (1555) Economy of the Habsburg monarchy refers to economic development and financial policies of the Habsburg monarchy, until the creation of the Austrian Empire in 1804. Centr...

 

石井道子

この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。 出典を追加して記事の信頼性向上にご協力ください。（このテンプレートの使い方）出典検索?: 石井道子 – ニュース · 書籍 · スカラー · CiNii · J-STAGE · NDL · dlib.jp · ジャパンサーチ · TWL (2016年10月) 石井 道子（いしい みちこ、1933年2月5日 - 2012年12...

Oravské Beskydy

Mountain range in Slovakia See also: Żywiec Beskids Babia Góra, a mountain in the range Oravské Beskydy (Hungarian: Árvai-Beszkidek) is a range of mountains straddling the northern-Slovakia-southern-Poland border, considered part of the Central Beskids, within the Outer Western Carpathians.[1] The highest mountain of the range is Babia Góra (1,725 metres [5,659 ft]), the center of the Babia Góra National Park, one of the first biosphere reserves established worldwide. Refer...

 

Monte Gazzo

Monte GazzoStato Italia Regione Liguria Provincia Genova Altezza419 m s.l.m. CatenaAppennino ligure Coordinate44°26′31.4″N 8°50′52.53″E44°26′31.4″N, 8°50′52.53″E Mappa di localizzazioneMonte Gazzo Modifica dati su Wikidata · Manuale Monte GazzoTipo di areaSIC Class. internaz.IT1331615 Stati Italia Regioni Liguria Province Genova Provvedimenti istitutivilegge regionale n. 28/2009 della Regione Liguria (10/7/2009) Disposizioni per la ...