ĺ˛çˇćłďźăăŁăăăťăďźăžăăŻăťăŤăłăćł[1]ďźčą: secant methodďźă¨ăŻăćąć šă˘ăŤă´ăŞăşă ăŽä¸ç¨Žă§ăăăďźĺ˛çˇă¨ăŻć˛çˇä¸ăŽ2çšäťĽä¸ă¨äş¤ăăç´çˇăŽăă¨ăďź
ĺ˛çˇćł
![]() ĺ˛çˇćłăŤăăĺ垊ăŽć§ĺăĺ˛çˇăŽĺçă揥ăŽĺ¤ă¨ĺŻžĺżăăă
ĺ˛çˇćłăŤăăĺ垊ăŽć§ĺăĺ˛çˇăŽĺçă揥ăŽĺ¤ă¨ĺŻžĺżăăă
éçˇĺ˝˘ćšç¨ĺź f (x) = 0 ăŽč§Ł x∗ ă1ă¤ćąăăă¨ăăďźĺż
čŚăŞăäşĺćłăŞăŠăç¨ăăŚďźĺĺăŤčżăĺćĺ¤ x0, x1 ăé¸ăłă揥ăŽĺ垊č¨çŽăăăăă¨ă§ x∗ ăŽčżäźźĺ¤ăćąăăă

é˘ć° f ă2ĺéŁçśĺžŽĺĺŻč˝ă§ f ′(x∗) â 0 ă㤠f ″(x∗) â 0 ăŞăă°ć°ĺ xk 㯠x∗ ăŤĺćăăăăŽĺć揥ć°ďźčąčŞçďźăŻ ϕ = (1 + √5)/2 ≈ 1.6 ă§ăă[2]ă
ăăĽăźăăłćłă¨ăŽé˘äż
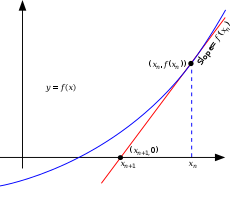 ăăĽăźăăłćłăŤăăĺ垊ăŽć§ĺăćĽçˇăŽĺçă揥ăŽĺ¤ă¨ĺŻžĺżăăă
ăăĽăźăăłćłăŤăăĺ垊ăŽć§ĺăćĽçˇăŽĺçă揥ăŽĺ¤ă¨ĺŻžĺżăăă
ĺ˛çˇćłăŻăăĽăźăăłćłăŽĺ垊č¨çŽ

ăŤçžăă垎ĺäżć° f ′(xk) ăč¨çŽăăăŤ

ăŤăăŁăŚĺˇŽĺĺă§čżäźźăăďźĺšžä˝ĺŚçăŤăŻćĽçˇăĺ˛çˇă§äťŁćżăăďźćšćłăŤç¸ĺ˝ăăă
ĺç´ăŤĺˇŽĺčżäźźăăă ăăŽăăĽăźăăłćłă¨ćŻčźăăă¨ăĺ˛çˇćłăŻĺćăžă§ăŽĺ垊ć°ăŻĺ˘ăăăă1ĺ垊ăăăăŽé˘ć°čŠäžĄĺć°ăŻĺ°ăŞăăăăăăŁăŚçˇćźçŽéăŤĺŻžăé˘ć°čŠäžĄăłăšăăŽĺ ăăĺ˛ĺă大ăăĺ ´ĺăŤăŻăĺćăžă§ăŽč¨çŽćéăç縎ă§ăăăă¨ăăăă
ĺčćçŽ
é˘éŁé
çŽ
ĺ¤é¨ăŞăłăŻ
ĺçť