Spinore
|
Read other articles:

Untuk kapal lain dengan nama serupa, lihat Kapal perusak Jepang Sazanami. Sazanami pada 15 April 1940 Sejarah Kekaisaran Jepang Nama SazanamiAsal nama Kapal perusak Jepang Sazanami (1899)Dipesan 1923 (tahun fiskal)Pembangun Arsenal Angkatan Laut MaizuruNomor galangan Perusak No. 53Pasang lunas 21 Maret 1930Diluncurkan 6 Juni 1931Mulai berlayar 19 Mei 1932Dicoret 10 Maret 1944Nasib Tenggelam pada 14 Januari 1944 Ciri-ciri umum Kelas dan jenis Kapal perusak kelas-FubukiBerat benaman 1...

First Chief Minister of Sikkim Lhendup Dorjee KhangsarpaOfficial Portrait, 1974First Chief Minister of SikkimIn office16 May 1975 – 18 August 1979GovernorB. B. LalPreceded byOffice createdSucceeded byNar Bahadur BhandariPrime Minister of SikkimIn office23 July 1974 – 16 May 1975MonarchPalden Thondup NamgyalPreceded bypost established; Brajbir Saran Das as Chief Administration OfficerSucceeded byoffice abolishedExecutive Council of SikkimIn office1967–1970MonarchPalden Thondup NamgyalCon...

Madyan atau Midian (Arab: مدين, Madyan; Ibrani: מִדְיָן, Madyan; Yunani: Μαδιάμ, Μαδιανίτης, Madianites, untuk orang Midian, Inggris: Midian) adalah sebuah tempat geografis yang disebutkan di dalam Alkitab Ibrani, Alkitab Kristen, Injil dan Al-Qur'an. Madyan diyakini terletak disebelah barat laut Hijaz dipantai timur dari Teluk Aqaba[1] dan ke arah utara Laut Merah,[2] tepatnya di daerah Al-Bad'. Etimologi Negeri Madyan diambil dari nama ...

Ordo Elang HitamBintang dari Ordo Elang HitamTipeState Order (dulunya) House Order (sekarang)Dibentuk17 Januari 1701MottoSuum Cuique (idiomatika-nya, untuk setiap orang menurut sumbangsihnya)KelayakanAnggota dari wangsa yang memerintah, pejabat senior militer dan sipil dan figur-figur lain yang terhormat yang ditunjuk oleh Raja PrusiaDianugerahkan kepadaPenghargaan sipil atau militerStatusGrand MasterTingkatKesatriaStatistikPenganugerahan pertama1701Jumlah penerima407 (sampai 1918)PrioritasTi...

Souliote War (1789–1793)Part of the Russo-Turkish War (1787–1792)Ali PashaDateFebruary 1789 – April 1793LocationSouliot ConfederationPashalik of YaninaResult Souliote victoryBelligerents Souliotes Ibrahim Pasha of Vlorë Mustafa Pasha of Delvinë Cham aghas Gjirokastër beys Pashalik of YaninaCommanders and leaders Georgios Botsaris Lambros Tzavelas Ibrahim Pasha of Vlorë Mustafa Pasha of Delvinë Ali Pasha of IoanninaStrength 10,000–20,000 vteRusso-Turkish War (1787–1792)Austro-Tu...
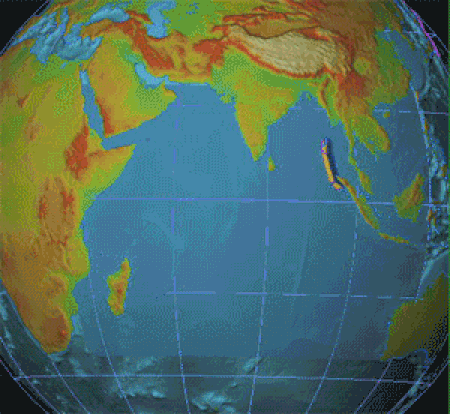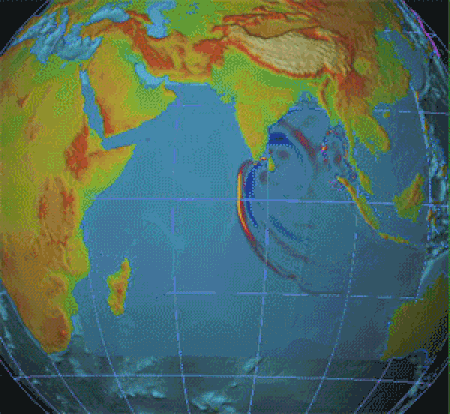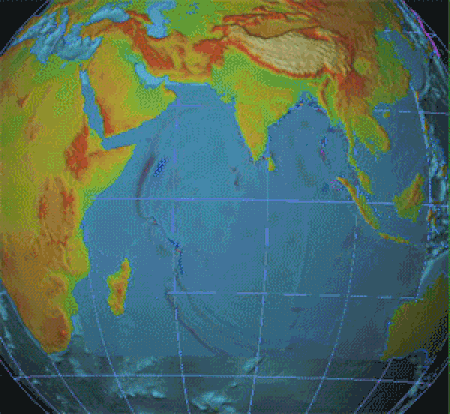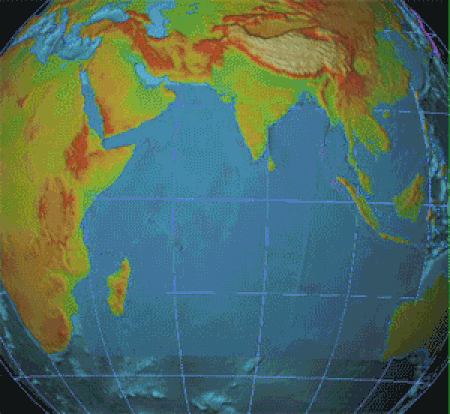
◄ Dezembro ► Dom Seg Ter Qua Qui Sex Sáb 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 1 2 3 4 Ano: 2024 Década: 2020 Século: XXI Milênio: 3.º 26 de dezembro é o 360.º dia do ano no calendário gregoriano (361.º em anos bissextos). Faltam 5 dias para acabar o ano. Eventos históricos 1972: Operação Linebacker II 2004: Sismo e tsunami do Oceano Índico 0887 — Berengário I é eleito rei da Itália pelos senhores da Lombardia. É coroado co...

PT Victoria Insurance TbkJenisPublikKode emitenIDX: VINSIndustriJasa keuanganDidirikan1978KantorpusatJakarta, IndonesiaTokohkunciSuwandi Suharto (Presiden Direktur)ProdukasuransiPendapatanRp 33,9 miliar (2017), Rp 25 miliar (2018) Laba bersihRp 8,8 miliar (2017), Rp 3,9 miliar (2018) Karyawan41 orang (2018)Situs webwww.victoriainsurance.co.id Victoria Insurance merupakan perusahaan publik yang bergerak dalam bidang asuransi dan bermarkas di Jakarta, Indonesia. Perusahaan ini didirikan pada ta...

Željko Komšić Anggota Kepresidenan Bosnia dan Herzegovina dari etnis KroasiaPetahanaMulai menjabat 20 November 2018Perdana MenteriDenis ZvizdićPendahuluDragan ČovićPenggantiPetahanaMasa jabatan6 November 2006 – 17 November 2014Perdana MenteriAdnan TerzićNikola ŠpirićVjekoslav BevandaPendahuluIvo Miro JovićPenggantiDragan ČovićAnggota Dewan Perwakilan Bosnia dan HerzegovinaMasa jabatan9 Desember 2014 – 20 November 2018Ketua Kepresidenan Bosnia dan Herzegov...

American comics superhero, created 1939 Comics character SamsonSamson, on the cover of Fantastic Comics #1 (1939).Publication informationPublisherFox Feature SyndicateFirst appearanceFantastic Comics #1 (Dec. 1939)Created byWill Eisner (writer, uncredited)Alex Blum (artist, as Alex Boon)In-story informationSpeciesHumanAbilitiesSuperhuman strength and enduranceInvunerability Samson is a superhero who appeared in comic books published by Fox Feature Syndicate. He first appeared in Fantastic Com...

Transportation system Leeds trolleybus systemAn original Leeds trolleybus, ca. 1912.OperationLocaleLeeds, West Riding of Yorkshire, England Twentieth century era: 1911 (1911)–1928 (1928) Status Closed Routes Leeds–FarnleyGuiseley–Otley/Burley-in-Wharfedale Electrification *** V DC parallel overhead lines Depot(s) Kirkstall Road; Guiseley Twenty-first century era: NGT Status Cancelled Routes 3 Operator(s) New Generation Transport Electrification *** V DC parallel overhead ...

Voce principale: Unione Sportiva Città di Palermo. SSC PalermoStagione 1980-1981 Sport calcio Squadra Palermo Allenatore Fernando Veneranda, poi Vincenzo Urbani, poi Carmelo Di Bella Presidente Gaspare Gambino Serie B14º Coppa ItaliaPrimo turno Maggiori presenzeCampionato: Vailati (36) Miglior marcatoreCampionato: Calloni (11) StadioLa Favorita Abbonati3 080[1] 1979-1980 1981-1982 Si invita a seguire il modello di voce Questa voce raccoglie le informazioni riguardanti la ...

Questa voce sull'argomento stagioni delle società calcistiche italiane è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Voce principale: Unione Sportiva Fiumana. Unione Sportiva FiumanaStagione 1941-1942Sport calcio Squadra Fiumana Allenatore Angelo Piccaluga Presidente Carlo Descovich Serie B15º posto. Retrocessa in Serie C. Coppa ItaliaSedicesimi di finale. Maggiori presenzeCampionato: Poggi (2...

Soil type Solidago multiradiata, Erigeron aureus, and Adiantum aleuticum in rocky serpentine soil Serpentine soil is an uncommon soil type produced by weathered ultramafic rock such as peridotite and its metamorphic derivatives such as serpentinite. More precisely, serpentine soil contains minerals of the serpentine subgroup, especially antigorite, lizardite, and chrysotile or white asbestos, all of which are commonly found in ultramafic rocks. The term serpentine is commonly used to refer to...

烏克蘭總理Прем'єр-міністр України烏克蘭國徽現任杰尼斯·什米加尔自2020年3月4日任命者烏克蘭總統任期總統任命首任維托爾德·福金设立1991年11月后继职位無网站www.kmu.gov.ua/control/en/(英文) 乌克兰 乌克兰政府与政治系列条目 宪法 政府 总统 弗拉基米尔·泽连斯基 總統辦公室 国家安全与国防事务委员会 总统代表(英语:Representatives of the President of Ukraine) 总...

English computer scientist (1912–1954) Turing redirects here. For other uses, see Turing (disambiguation). Alan TuringOBE FRSTuring in 1936BornAlan Mathison Turing(1912-06-23)23 June 1912Maida Vale, London, EnglandDied7 June 1954(1954-06-07) (aged 41)Wilmslow, Cheshire, EnglandCause of deathCyanide poisoning as an act of suicide[note 1]Alma mater University of Cambridge (BA, MA) Princeton University (PhD) Known for Cryptanalysis of the Enigma Turing's proof T...

BagratuniWangsa indukDinasti OrontidNegaraArmeniaAlbania KaukasiaKelompok etnisArmeniaDidirikan100 SMPendiriAshot IPenguasa terakhirGagik IIGelar Raja Armenia Raja Albania Raja Vaspurakan Raja Syunik Raja Lori Raja Artsakh Pangeran Vanand Pangeran Taron Pangeran Khachen Cabang kadetRubenid (kemungkinan)Hasan-Jalalyan (tidak langsung) Bagratuni atau Bagratid (bahasa Armenia: Բագրատունի) adalah keluarga kerajaan Armenia yang menguasai berbagai negara di wilayah Kerajaan Armenia pa...

Reconstructed ancestor of the Berber languages Proto-BerberProto-LibyanReconstruction ofBerber languagesRegionNorth AfricaReconstructedancestorProto-Afroasiatic Proto-Berber or Proto-Libyan is the reconstructed proto-language from which the modern Berber languages descend. Proto-Berber was an Afroasiatic language, and thus its descendant Berber languages are cousins to the Egyptian language, Cushitic languages, Semitic languages, Chadic languages, and the Omotic languages.[1] His...

Эта страна Автор Фигль-Мигль Жанр Русская литература, отечественный детектив Язык оригинала русский Оригинал издан 2017 Издатель Лимбус Пресс Выпуск 2017 Страниц 376 ISBN 978-5-8370-0812-2 «Эта страна» — роман, детектив писателя современной русской литературы Фигль-Мигль. Ром...

Sebagian dari akropolis yang telah digali Kaminaljuyu adalah sebuah situs peradaban Maya pada zaman pra-Kolumbus. Kota Kaminaljuyu terkubur di bawah Kota Guatemala. Situs ini telah disebut-sebut sebagai salah satu situs arkeologi terbesar di benua Amerika oleh Michael Coe,[1] walaupun peninggalan-peninggalan yang tersisa saat ini (beberapa gundukan) tidak terlihat begitu menarik bila dibandingkan dengan situs-situs Maya lainnya yang sering didatangi wisatawan. Situs ini pertama kali d...

1972 American TV series or program The Corner BarGabriel Dell as Harry Grant, 1972GenreSitcomWritten byNorman BaraschDirected byPeter BaldwinRick EdelsteinStarringGabriel Dell (season 1)Anne Meara (season 2)Eugene Roche (season 2)J. J. BarryShimen RuskinBill FioreCountry of originUnited StatesOriginal languageEnglishNo. of seasons2No. of episodes16ProductionRunning time30 minutesProduction companyAlan King ProductionsOriginal releaseNetworkABCReleaseJune 21, 1972 (1972-06-21) –Sep...




