Profondità (algebra)
|
Read other articles:

Alexei Ivanovich RadzievskyLahir(1911-07-31)31 Juli 1911Uman, Cherkasy, UkrainaMeninggal1978Pengabdian USSRDinas/cabangTentara MerahAngkatan Darat SovietLama dinas1929–1978 Alexei Ivanovich Radzievsky (kelahiran 13 Agustus 1911 - wafat 1978) adalah seorang prajurit profesional Uni Soviet yang berjuang pada Perang Dunia II. Ia kemudian menulis karya-karya tentang strategi militer.[1] Catatan ^ Радзиевский Алексей Иванович Pengawasan otoritas Umum ISNI 1...

Family of caddisflies Philopotamidae Dolophilodes sp. larva Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Arthropoda Class: Insecta Order: Trichoptera Suborder: Annulipalpia Superfamily: Philopotamoidea Family: PhilopotamidaeStephens, 1829 Subfamilies see text Philopotamidae is a family of insects in the order Trichoptera, the caddisflies. They are known commonly as the finger-net caddisflies.[1][2] The aquatic larvae of these caddisflies spin mesh nets...

Questa voce sull'argomento centri abitati della Romania è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. ValcanicomuneLocalizzazioneStato Romania Regione Banato Distretto Timiș TerritorioCoordinate46°00′N 20°24′E / 46°N 20.4°E46; 20.4 (Valcani)Coordinate: 46°00′N 20°24′E / 46°N 20.4°E46; 20.4 (Valcani) Altitudine76 m s.l.m. Su...

Sekolah Tinggi Manajemen Informatika dan Komputer PrabumulihJenisPerguruan tinggi swastaLokasiJl. Patra No.50, Kota Prabumulih, Sumatera Selatan 31111, Prabumulih, IndonesiaNama julukanSTMIK PrabumulihSitus webwww.stmikypprabumulih.ac.id Sekolah Tinggi Manajemen Informatika dan Komputer Prabumulih (disingkat STMIK Prabumulih) adalah sebuah perguruan tinggi swasta di Kota Prabumulih[1] yang dimiliki oleh sekolah tinggi swasta Yayasan Pendidikan Prabumulih (YPP Prabumulih) Wacana Pemeri...

Sculpture by Keith Haring in Berlin, Germany The BoxersThe sculpture in 2008ArtistKeith HaringYear1987 (1987)LocationBerlin, GermanyCoordinates52°30′32″N 13°22′19″E / 52.508767°N 13.371814°E / 52.508767; 13.371814 The Boxers is an outdoor 1987 steel and lacquer sculpture by Keith Haring, installed in Berlin, Germany.[1][2] Description The sculpture shows simplified humanoid figures, one red and one blue, with holes in the head and stoma...

Paranormal terminology and recordings A waveform of white noise plotted on a graph Part of a series on theParanormal Main articles Astral projection Astrology Aura Bilocation Breatharianism Clairvoyance Close encounter Cold spot Crystal gazing Conjuration Cryptozoology Demonic possession Demonology Ectoplasm Electronic voice phenomenon Exorcism Extrasensory perception Forteana Fortune-telling Ghost hunting Magic Mediumship Miracle Occult Orb Ouija Paranormal fiction Paranormal television Prec...

Condition of a nation with self-governance Not to be confused with Interdependence. For other uses, see Independence (disambiguation). The Thirteen British Colonies on the east coast of North America issued a Declaration of Independence in 1776 Chile, one of several Spanish territories in South America, issued a Declaration of independence in 1818 Prince Pedro surrounded by a crowd in São Paulo after breaking the news of Brazil's independence on 7 September 1822. The Finnish Senate of 1917, ...

Genus of birds This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Leptopogon – news · newspapers · books · scholar · JSTOR (January 2021) (Learn how and when to remove this message) Leptopogon Slaty-capped flycatcher(L. superciliaris) Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Chordat...

Russian ballet dancer (1933–2020) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Nikolai Fadeyechev – news · newspapers · books · scholar · JSTOR (November 2022) (Learn how and when to remove this message) Nikolai FadeyechevNikolai Fadeyechev and Maya Plisetskaya in Swan Lake, Milan, 1964BornNikolai Boris...

2014 studio album by the VampsMeet the VampsStudio album by the VampsReleased11 April 2014Recorded2012–2013GenrePop[1]pop rock[2]folk pop[3]Length51:00LabelVirgin EMIProducer TMS Espionage The Vamps chronology Meet the Vamps(2014) Somebody to You(2014) The Vamps studio album chronology Meet the Vamps(2014) Wake Up(2015) Alternative coverDeluxe edition cover Singles from Meet the Vamps Can We DanceReleased: 6 August 2013 Wild HeartReleased: 19 January 2014 Las...

Japanese nativist scholar and priest (1797–1870) You can help expand this article with text translated from the corresponding article in Japanese. (January 2022) Click [show] for important translation instructions. Machine translation, like DeepL or Google Translate, is a useful starting point for translations, but translators must revise errors as necessary and confirm that the translation is accurate, rather than simply copy-pasting machine-translated text into the English Wikipedia....

本表是動態列表,或許永遠不會完結。歡迎您參考可靠來源來查漏補缺。 潛伏於中華民國國軍中的中共間諜列表收錄根據公開資料來源,曾潛伏於中華民國國軍、被中國共產黨聲稱或承認,或者遭中華民國政府調查審判,為中華人民共和國和中國人民解放軍進行間諜行為的人物。以下列表以現今可查知時間為準,正確的間諜活動或洩漏機密時間可能早於或晚於以下所歸�...

Messier 65Foto M65 dari Teleskop luar angkasa Hubble Kredit: NASA/STScI/WikiSkyData pengamatan (J2000 epos)Rasi bintangLeoAsensio rekta 11j 18m 55.9d[1]Deklinasi +13° 05′ 32″[1]Pergeseran merah0.002692Kecepatan radial helio807Kecepatan galaktosentrik723Magnitudo semu (V)10.25[1]Penamaan lainNGC 3623,[1] UGC 6328,[1] PGC 34612[1] Messier 65 (juga dikenal sebagai NGC 3623) adalah sebuah galaksi spiral meneng...

Not to be confused with Canaan (village), Connecticut in the town of North Canaan, Connecticut. Town in Connecticut, United StatesCanaan, ConnecticutTownTown of CanaanSouth Canaan Congregational Church Seal Litchfield County and Connecticut Northwest Hills Planning Region and ConnecticutShow CanaanShow ConnecticutShow the United StatesCoordinates: 41°57′42″N 73°18′30″W / 41.96167°N 73.30833°W / 41.96167; -73.30833Country United StatesU.S. sta...

Spanish footballer In this Spanish name, the first or paternal surname is Ontiveros and the second or maternal family name is Parra. Javi Ontiveros Ontiveros with Spain U18 in 2015Personal informationFull name Javier Ontiveros Parra[1]Date of birth (1997-09-09) 9 September 1997 (age 26)[1]Place of birth Marbella, SpainHeight 1.70 m (5 ft 7 in)[1]Position(s) WingerTeam informationCurrent team CádizYouth career2000–2008 Vázquez Cultural200...

Pour l’article homonyme, voir Constitution polonaise du 3 mai 1791. Si ce bandeau n'est plus pertinent, retirez-le. Cliquez ici pour en savoir plus. Certaines informations figurant dans cet article ou cette section devraient être mieux reliées aux sources mentionnées dans les sections « Bibliographie », « Sources » ou « Liens externes » (février 2017). Vous pouvez améliorer la vérifiabilité en associant ces informations à des références à l'ai...
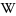
توثيق القالب[عرض] [عدّل] [تاريخ] [محو الاختزان] [استخدامات] هذا القالب يستعمل لوا: وحدة:بطاقة/قالب/موقع ويب استعمال {{بطاقة موقع ويب |اسم= |اسم اصلي= |شعار = | لقطة شاشة = | عنوان= | شعار نصي= | تجاري= | نوع= | مؤلف= | بلد= | تأسيس= | تاريخ الإطلاق= | تاريخ_الاختفاء= | الح�...

Immagine di un lanciatore sovietico Sojuz. Questi lanciatori sono stati i primi razzi a mandare degli oggetti nello spazio Dalla seconda guerra mondiale fino alla dissoluzione dell'Unione Sovietica, il programma spaziale sovietico ha deciso lo sviluppo dei lanciatori, delle sonde e degli strumenti per la guerra e l'esplorazione spaziale. Il programma spaziale sovietico è sempre stato coperto dal segreto. Il leader del programma Sergej Pavlovič Korolëv era indicato solamente come il capo pr...

Mushaga BakengaNazionalità Norvegia Altezza181 cm Calcio RuoloAttaccante Squadra Punjab FC CarrieraGiovanili 2007-2008 Rosenborg Squadre di club1 2009-2011 Rosenborg34 (12)2012 Club Bruges8 (1)2012-2013→ Cercle Bruges27 (7)2013 Club Bruges0 (0)2013-2014→ Esbjerg24 (6)2014-2015→ Eintracht Braunschweig17 (2)2015-2016→ Molde8 (2)2016-2017 Rosenborg21 (8)2017-2019 Tromsø41 (5)2019→ Ranheim12 (2)2020-2021 Odd37 ...

Attack of US Senator by a Representative Caning of Charles SumnerPolitical caricature of the caning, depicting Sumner on the floor holding a pen and his Crime against Kansas speech as Brooks lunges at himLocationOld Senate Chamber, United States Capitol, Washington, D.C.DateMay 22, 1856; 168 years ago (1856-05-22)TargetCharles SumnerAttack typeAssault by caningPerpetratorPreston Smith BrooksMotiveRetaliation to an anti-slavery speech by SumnerVerdictGuiltyConvictionsAssaultS...











![{\displaystyle A=M=K[x,y,z]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/54a2d6d1d37fbea7997e4d42a9d63c8bcd208bbf)



























