Dominio di Krull
|
Read other articles:

Political culture where facts are considered irrelevant A major contributor to this article appears to have a close connection with its subject. It may require cleanup to comply with Wikipedia's content policies, particularly neutral point of view. Please discuss further on the talk page. (March 2024) (Learn how and when to remove this template message) Post-truth politics (which some commentators prefer to call post-factual politics[1] or post-reality politics[2]), amidst var...

American politician For other people with similar names, see Wild Bill (disambiguation) and William Hickman (disambiguation). This section needs additional citations for verification. Relevant discussion may be found on the talk page. Please help improve this article by adding citations to reliable sources in this section. Unsourced material may be challenged and removed. (August 2013) (Learn how and when to remove this template message) Wild Bill HickmanHickman c. 1860BornWilliam A...

Television channel in Australia For other uses, see CMC (disambiguation). Television channel CMT AustraliaCountryAustraliaProgrammingLanguage(s)EnglishOwnershipOwnerParamount Networks UK & AustraliaSister channelsSister channelsHistoryLaunched1 July 2020Former namesCountry Music Channel (2004–2020)AvailabilityStreaming mediaFoxtel GoChannel 805 CMT Australia is an Australian cable and satellite music television channel owned and operated by Paramount Networks UK & Australia. It is t...

Questa voce o sezione sull'argomento sportivi non è ancora formattata secondo gli standard. Commento: Numerosissimi overlink. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. George Foreman George Foreman nel 2016 Nazionalità Stati Uniti Altezza 192 cm Peso 118 kg Pugilato Categoria Pesi massimi Termine carriera 22 novembre 1997 Carriera Incontri disputati Totali 81 Vinti (KO) 76 (68) Persi (KO) 5 (1) Pareggiati 0 ...

Colombian lawyer, general and political figure Eustorgio Salgar10th President of the United States of ColombiaIn officeApril 1, 1870 – April 1, 1872Preceded bySantos GutiérrezSucceeded byManuel Murillo ToroPresiding Member of the Provisional Executive Ministry of the ColombiaIn officeFebruary 9, 1863 – May 14, 1863Serving with Santos Gutiérrez, José Hilario López, Froilan Largacha, Tomás Cipriano de MosqueraPreceded byProvisionary Office*Succeeded byProv...
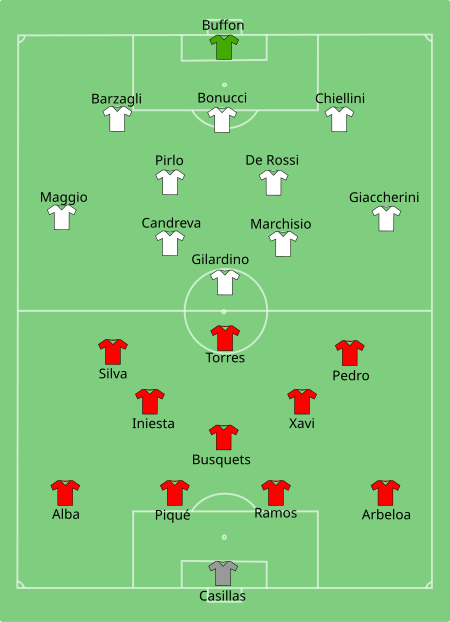
The knockout stage of the 2013 FIFA Confederations Cup began on 26 June with the semi-final round, and concluded on 30 June 2013 with the final at the Estádio do Maracanã, Rio de Janeiro. The top two teams from each group advanced to the knockout stage to compete in a single-elimination style tournament. A third place match was included and played between the two losing teams of the semi-finals. In the knockout stage (including the final), if a match was level at the end of 90 minutes, ext...

جزء من سلسلة مقالات حولالشعب الفلسطيني التركيبة السكانية الهوية فلسطين التاريخ الاسم الشعب النكبة الشتات مخيمات اللجوء السياسةسابق اللجنة العربية العليا القرى المهجرة محمية عموم فلسطين حكومة عموم فلسطين الفدائيون م.ت.ف السلطة الوطنية (س.و.ف) الأحزاب السياسية حالي فتح حم�...

Indian literature Further information: Meitei classical language movement and Meitei linguistic purism movement You can help expand this article with text translated from the corresponding article in Manipuri. Click [show] for important translation instructions. Do not translate text that appears unreliable or low-quality. If possible, verify the text with references provided in the foreign-language article. You must provide copyright attribution in the edit summary accompanying your translat...

ХристианствоБиблия Ветхий Завет Новый Завет Евангелие Десять заповедей Нагорная проповедь Апокрифы Бог, Троица Бог Отец Иисус Христос Святой Дух История христианства Апостолы Хронология христианства Раннее христианство Гностическое христианство Вселенские соборы Н...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Fox Sports Houston – news · newspapers · books · scholar · JSTOR (July 2021) (Learn how and when to remove this message) Television channel Fox Sports HoustonFinal Fox Sports Houston logo, used from September 1 to October 5, 2012.CountryUnited StatesBroadcast a...

Nikolas Nartey Nazionalità Danimarca Altezza 183 cm Peso 75 kg Calcio Ruolo Centrocampista Squadra Stoccarda CarrieraGiovanili 2008-2013 Aalborg2013-2017 Copenaghen2017-2018 ColoniaSquadre di club1 2017-2019 Colonia II27 (3)2017-2019 Colonia2 (0)2019 Stoccarda0 (0)2019-2020→ Hansa Rostock19 (1)2020-2021→ Sandhausen24 (0)2021- Stoccarda17 (0)Nazionale 2015-2016 Danimarca U-165 (0)2016-2017 Danimarca U-1711 (6)2017-2018 Danimarca ...

烏克蘭總理Прем'єр-міністр України烏克蘭國徽現任杰尼斯·什米加尔自2020年3月4日任命者烏克蘭總統任期總統任命首任維托爾德·福金设立1991年11月后继职位無网站www.kmu.gov.ua/control/en/(英文) 乌克兰 乌克兰政府与政治系列条目 宪法 政府 总统 弗拉基米尔·泽连斯基 總統辦公室 国家安全与国防事务委员会 总统代表(英语:Representatives of the President of Ukraine) 总...

Disambiguazione – Se stai cercando la Nazionale maschile, vedi Nazionale di pallacanestro della Svezia. Questa voce sull'argomento nazionali di pallacanestro è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Svezia Uniformi di gara Casa Trasferta Sport Pallacanestro Federazione Federazione cestistica della Svezia Confederazione FIBA (dal 1952) Zona FIBA FIBA Europe Allenatore Marco Crespi Ranking FIBA 42º FIBA EuroBasket Women Partecipazioni 7 Medagl...

جزء من سلسلة مقالات حولالله في الإسلام مصطلحاتالتسبيح: سبحان الله التكبير: الله أكبر الحمد: الحمد لله التشهّد: لا إله إلّا الله تعابير مرتبطة جلَّ جلاله سبحانه وتعالى عزَّ وجلّ أخرى إنَّا لله بسم الله إن شاء الله ما شاء الله استغفر الله لا حول ولا قوة إلا بالله جزاك الله أعو�...

Si ce bandeau n'est plus pertinent, retirez-le. Cliquez ici pour en savoir plus. Cet article ne cite pas suffisamment ses sources (avril 2021). Si vous disposez d'ouvrages ou d'articles de référence ou si vous connaissez des sites web de qualité traitant du thème abordé ici, merci de compléter l'article en donnant les références utiles à sa vérifiabilité et en les liant à la section « Notes et références ». En pratique : Quelles sources sont attendues ? Com...

战俘营奥运会全称中国人民志愿军碧潼战俘营奥林匹克运动会,是朝鲜战争时期在中国人民志愿军朝鲜碧潼戰俘營举办的模拟奥运会。参赛运动员皆为联合国军战俘。 运动会 战俘营奥林匹克运动会于1952年11月15日至27日在朝鲜碧潼举行。有来自11个国家的约500名囚犯参加了比赛。[1]他们是朝鲜所有狱营的代表。并参加了美式足球、棒球、垒球、篮球、排球、田径、足球...

Place for a fire to heat the home and to cook food, usually of masonry This article is about home hearths. For industrial hearths, see open hearth furnace and industrial furnace. Hearth room redirects here. For the album by Frost Children, see Hearth Room. Look up hearth in Wiktionary, the free dictionary. Hearth with cooking utensils A hearth (/hɑːrθ/) is the place in a home where a fire is or was traditionally kept for home heating and for cooking, usually constituted by at least a horiz...

倫敦的一個垃圾搜尋者 垃圾搜尋(dumpster diving)、垃圾桶尋寶、翻垃圾桶等,是指從別人拋棄的東西(有時不一定是垃圾桶)中收集自己有用的東西(例如食物)作為自己用途。進行這種行為的人不一定是因為貧窮,部份人是為了響應環境保護意識,更有部份人是以抗議及痛心資本主義社會的浪費;甚至有視之為嗜好者。 垃圾搜尋是一種行為,從垃圾堆中搜尋個人喜好的「寶�...

Голод в Крыму Картина «Голод в Крыму» Николая Самокиша, 1923 год Причина советская экономическая политика, последствия гражданской войны, неурожай Страна РСФСР СССР Место Крымская АССР Период весна 1921 — лето 1923 Умерло от голода До 100 000 человек Медиафайлы на Ви�...

2012 في البرازيلمعلومات عامةالسنة 2012 البلد البرازيل 2011 في البرازيل 2013 في البرازيل تعديل - تعديل مصدري - تعديل ويكي بيانات سنوات 2010 2011 2012 2013 2014 علم البرازيل الجدول الزمني لتاريخ البرازيل فيما يلي قوائم الأحداث التي وقعت خلال عام 2012 في البرازيل. رياضة 1 يناير – الدوري البرازيلي ...









![{\displaystyle A[\mathbf {X} ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/087ee6801e37019b65cbb3e4014168f9ffd480a9)
![{\displaystyle A[[\mathbf {X} ]]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1eb800c083d14a3918362f1bcc1266c9008250c3)
![{\displaystyle K[X,Y]/(X^{2}-Y^{3})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d482edcfc5763ebdb117d0d67ea339463e0a4fcd)









