Logaritmo naturale
|
Read other articles:

Abul Kalam Azadابول کلام آزاد Menteri Pendidikan IndiaMasa jabatan15 Agustus 1947 – 2 Februari 1958Perdana MenteriJawaharlal Nehru Informasi pribadiLahir(1888-11-11)11 November 1888Mekkah, Hejaz Vilayet, Kekaisaran Ottoman (sekarang Arab Saudi)Meninggal22 Februari 1958(1958-02-22) (umur 69)Delhi, IndiaKebangsaanIndiaPartai politikKongres Nasional IndiaSuami/istriZulaikha BegumPenghargaan sipilBharat RatnaTanda tanganSunting kotak info • L • B Abul Kal...

Uncontrolled nuclear fission chain reaction A criticality accident is an accidental uncontrolled nuclear fission chain reaction. It is sometimes referred to as a critical excursion, critical power excursion, divergent chain reaction, or simply critical. Any such event involves the unintended accumulation or arrangement of a critical mass of fissile material, for example enriched uranium or plutonium. Criticality accidents can release potentially fatal radiation doses if they occur in an unpro...

Family of mammals Balaenidae[1]Temporal range: Miocene to present Montage of two extant balaenids, Balaena mysticetus (right) and Eubalaena australis (left) Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Chordata Class: Mammalia Order: Artiodactyla Infraorder: Cetacea Parvorder: Mysticeti Family: BalaenidaeGray, 1821 Type genus BalaenaLinnaeus, 1758 Genera Balaena Eubalaena †Antwerpibalaena †Archaeobalaena[2] †Balaenella †Balaenula †Balaenotus ...

Baltic German architect Christoph HaberlandBorn(1750-01-01)1 January 1750Riga, Russian EmpireDied7 March 1803(1803-03-07) (aged 53)Riga, Russian EmpireNationalityBaltic GermanKnown forArchitectureMovementClassicism Christoph Haberland (Latvian: Kristofs Hāberlands) was a Baltic German architect, chief architect of Riga and is considered one of the most illustrious masters of classical architecture in Latvian history. Biography Christoph Haberland was born in Riga to a mason on 1 Ja...

Annapurna Pictures, LLCJenisSwastaIndustriFilmDidirikan1 April 2011; 13 tahun lalu (2011-04-01)PendiriMegan EllisonKantorpusatLos Angeles, California, Amerika SerikatTokohkunciLarry Ellison (Ketua dan Pemilik)Jasa Pembuatan film distribusi film produksi televisi pengembang permainan video PemilikLarry Ellison[1]Anakusaha Annapurna International Annapurna Television Annapurna Interactive Mirror (usaha patungan dengan Metro-Goldwyn-Mayer) Situs webwww.annapurna.pictures Annapurna Pictures adal...

South Korean basketball player Park Ji-hyunPark Ji-hyun (2020)No. 1 – Asan Woori Bank WooriWONPositionGuardLeagueWKBLPersonal informationBorn (2000-04-07) 7 April 2000 (age 24)Seongnam, South KoreaNationalitySouth KoreanListed height6 ft 1 in (1.85 m)Career informationPlaying career2018–presentCareer history2018–presentAsan Woori Bank Wibee / WooriWON Career highlights and awards WKBL Rookie of the Year (2019) Medals Women's basketball Representing Sout...

Railway tunnel in Montreal, Quebec, Canada This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Mount Royal Tunnel – news · newspapers · books · scholar · JSTOR (May 2008) (Learn how and when to remove this message) Mount Royal TunnelLooking east towards the portal of the Mount Royal Tunnel and Jean Talon Street ...
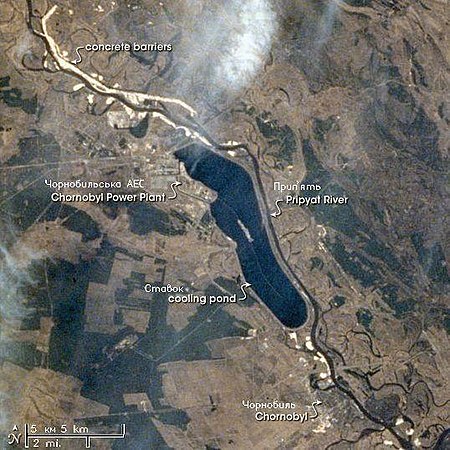
Decommissioned nuclear power plant in Ukraine Chernobyl Nuclear Power PlantView of the plant in 2013. From L to R New Safe Confinement under construction and reactors 4 to 1.Official nameSSE Chernobyl Nuclear Power PlantCountryUkraineLocationnear Pripyat, Kyiv OblastCoordinates51°23′21″N 30°05′58″E / 51.38917°N 30.09944°E / 51.38917; 30.09944StatusUndergoing DecommissioningConstruction began15 August 1972Commission date26 September 1977&...

Japanese folklorist Kunio Yanagita柳田 國男Kunio Yanagita, circa 1940BornKunio Matsuoka(1875-07-31)July 31, 1875Fukusaki, Hyōgo Prefecture, JapanDiedAugust 8, 1962(1962-08-08) (aged 87)Tokyo, JapanNationalityJapaneseOccupation(s)Bureaucrat, Folklorist, Scholar, WriterKnown forTōno Monogatari (遠野物語) Momotarō no Tanjō(桃太郎の誕生) Nihon mukashibanashi meii (Japanese Folk Tales)SpouseTaka Yanagita (1904)ParentYakusai Matsuoka (father) Naohei Yanagita (father-in-l...

American college football season 2012 Sam Houston State Bearkats footballSouthland co-championFCS Championship Game, L 13–39 vs. North Dakota StateConferenceSouthland ConferenceRankingSports NetworkNo. 2FCS CoachesNo. 2Record11–4 (6–1 Southland)Head coachWillie Fritz (3rd season)Offensive coordinatorDoug Ruse (1st season)Offensive schemeSpread optionDefensive coordinatorScott Stoker (4th season)Base defense3–3–5Home stadiumBowers Stadi...

Artikel ini berisi konten yang ditulis dengan gaya sebuah iklan. Bantulah memperbaiki artikel ini dengan menghapus konten yang dianggap sebagai spam dan pranala luar yang tidak sesuai, dan tambahkan konten ensiklopedis yang ditulis dari sudut pandang netral dan sesuai dengan kebijakan Wikipedia. (Desember 2020) Alumniportal DeutschlandDidirikanSeptember 2008Lokasi JermanOrang penting12 karyawan[1]Situs resmiwww.alumniportal-deutschland.org Alumniportal Deutschland adalah sebuah s...

Local government area in Queensland, AustraliaShire of TorresQueenslandPopulation3,421 (2021 census)[1] • Density3.8699/km2 (10.023/sq mi)Established1974Area884 km2 (341.3 sq mi)[2]MayorYen LobanCouncil seatThursday IslandRegionFar North QueenslandState electorate(s)CookFederal division(s)LeichhardtWebsiteShire of Torres LGAs around Shire of Torres: Papua New Guinea Torres Strait Island Region Papua New Guinea Torres Strait Shire of Torres Cora...

Questa voce sull'argomento cestisti neozelandesi è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Micaela CocksNazionalità Nuova Zelanda Altezza174 cm Peso69 kg Pallacanestro RuoloGuardia Squadra Free agent CarrieraGiovanili 2006-2010 Oregon Ducks Squadre di club 2010-2011 COB Calais2011-2018 Townsville Fire2019-2021Townsville Flames2021-2022 Townsville Fire2022Northern Kahu202...

Species of flowering plant in the gooseberry family Grossulariaceae Redcurrant Cultivated redcurrant Scientific classification Kingdom: Plantae Clade: Tracheophytes Clade: Angiosperms Clade: Eudicots Order: Saxifragales Family: Grossulariaceae Genus: Ribes Species: R. rubrum Binomial name Ribes rubrumL. 1753 not Torr. & A. Gray 1840 nor Hook. f. & Thomson 1858 Synonyms[1] List Grossularia rubra (L.) Scop. Ribes acidum Turcz. ex Pojark. Ribes hispidulum (Jancz.) Pojark. Ri...

Artikel ini sudah memiliki daftar referensi, bacaan terkait, atau pranala luar, tetapi sumbernya belum jelas karena belum menyertakan kutipan pada kalimat. Mohon tingkatkan kualitas artikel ini dengan memasukkan rujukan yang lebih mendetail bila perlu. (Pelajari cara dan kapan saatnya untuk menghapus pesan templat ini) Tak KudugaAlbum studio karya Ruth SahanayaDirilisDesember 1989Direkam1988-1989GenrePop, Dance, JazzLabelAquarius MusikindoKronologi Ruth Sahanaya Seputih Kasih (1986)Seputi...

Pour les articles homonymes, voir Gazier. Albert Gazier Fonctions Ministre de l'Information 17 mai 1958 – 1er juin 1958(15 jours) Président René Coty Président du Conseil Pierre Pflimlin Gouvernement Pflimlin Prédécesseur Robert Buron Successeur André Malraux 12 juillet 1950 – 11 août 1951(1 an et 30 jours) Président Vincent Auriol Président du Conseil René PlevenHenri Queuille Gouvernement Pleven IQueuille III Successeur Robert Buron Ministre des Affaires social...

Masataka TaketsuruLahir竹鶴 政孝たけつる まさたか20 Juni 1894Takehara, Hiroshima, JepangMeninggal29 Agustus 1979(1979-08-29) (umur 85)Bunkyō, Tokyo, JepangKebangsaanJepangAlmamaterUniversitas GlasgowUniversitas OsakaDikenal atasPendiri Nikka WhiskySuami/istriRita Taketsuru(1920.01.08-1961.01.17, kematiannya) Penghargaan Order of the Sacred Treasure, 3rd class (en) Masataka Taketsuru (竹鶴 政孝code: ja is deprecated , Taketsuru Masataka, 1894–1979) adalah seorang kim...

Cet article est une ébauche concernant l’architecture ou l’urbanisme et les Yvelines. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Écuries du roi puis de la ReineLa Grande Écurie du château de Versailles, prise depuis le pavillon Dufour.PrésentationDestination initiale écuriesDestination actuelle Cour d'appel de VersaillesConstruction 1672 (achat du terrain)Occupant Cour d'appel de VersaillesPatrimo...

Pour les articles homonymes, voir Colorado (homonymie). Colorado Sceau du Colorado. Drapeau du Colorado. Carte des États-Unis avec le Colorado en rouge.SurnomThe Centennial StateEn français : « l'État du centenaire ».DeviseNil sine numine (latin)« Rien sans la providence ». Administration Pays États-Unis Capitale Denver Adhésion à l’Union 1er août 1876 (148 ans) (38e État) Gouverneur Jared Polis (D) Sénateurs John Hickenlooper (D)Michael Benn...

Late form of ancient Greek religion Serapis, a Greco-Egyptian god worshipped in Hellenistic Egypt The concept of Hellenistic religion as the late form of Ancient Greek religion covers any of the various systems of beliefs and practices of the people who lived under the influence of ancient Greek culture during the Hellenistic period and the Roman Empire (c. 300 BCE to 300 CE). There was much continuity in Hellenistic religion: people continued to worship the Greek gods and to practice the sam...

























































