Insieme di Mandelbrot
|
Read other articles:

Takizo IwasakiLahir12 September 1895Meninggal1965Kebangsaan JepangDikenal atasPelopor makanan palsu Takizo Iwasaki (lahir 12 September 1895 dan meninggal sekitar tahun 1965 di usia 70 tahun) adalah seorang pengusaha makanan asal Jepang. Ia adalah pelopor terciptanya makanan palsu, instrumen pajangan makanan yang lazim ditemukan di restoran Jepang.[1] Kisah Takizo Iwasaki membuat makanan palsu berawal saat ia membuat Omurice palsu. Omurice adalah makanan Jepang yang dibuat menggu...

Serangan wilayah barat Soviet 1918–1919Bagian dari Perang Saudara Rusia, Perang Polandia-Soviet, Perang Kemerdekaan Estonia, Perang Kemerdekaan Latvia, Perang Kemerdekaan Lithuania, dan Perang Kemerdekaan UkrainaPoster propaganda anti-Polandia Soviet 1920Tanggal18 November 1918 – Maret 1919LokasiBelarus, Estonia, Latvia, Lithuania,Polandia, Rusia, UkrainaHasil Soviet defeatPihak terlibat Belarus Estonia Latvia Lituania Polandia Rumania Gerakan Putih Ukraina Britania Raya Ob...

Часть серии статей о Холокосте Идеология и политика Расовая гигиена · Расовый антисемитизм · Нацистская расовая политика · Нюрнбергские расовые законы Шоа Лагеря смерти Белжец · Дахау · Майданек · Малый Тростенец · Маутхаузен ·&...

Langit Sore adalah kelompok musik Indonesia yang didirikan di Yogyakarta pada tahun 2018. Grup ini dimotori oleh Arman Harjo, seorang musisi yang telah aktif menulis lagu sejak masa sekolah menengah pertama pada awal tahun 2000-an. Saat ini, anggota Langit Sore terdiri dari Arman Harjo, Plato Ginting, dan Cacha Scholastica. Langit Sore dikenal sebagai grup musik yang sangat produktif, dengan lebih dari seratus lagu yang telah dirilis sejak mereka pertama kali muncul. Mencerminkan dedikasi da...

This article is part of a series aboutGeorge Washington Early life Family Military career Electoral history American Revolution Virginia Association Commander in Chiefof the Continental Army Valley Forge Battle of Trenton Mount Vernon Conference 1787 Constitutional Convention 1st President of the United States Presidency (Timeline) First term 1788–89 election 1st inauguration Judiciary Act Whiskey Rebellion Thanksgiving Presidential title Coinage Act Residence Act District of Columbia Seco...

كأس أوروبا 1958–59أقيم النهائي على مرسيدس بنز أرينا في شتوتغارت.تفاصيل المسابقةالتواريخ26 أغسطس 1958 – 3 يونيو 1959الفرق28المراكز النهائيةالبطل ريال مدريدالوصيف ستاد ريمسإحصائيات المسابقةالمباريات الملعوبة55الأهداف المسجلة199 (3٫62 لكل مباراة)أفضل هداف جاست فونتين (10 أهداف)�...

Shopping mall in Georgia, United StatesCobb Center MallLocationSmyrna, Georgia, United StatesCoordinates33°54′00″N 84°32′31″W / 33.90000°N 84.54194°W / 33.90000; -84.54194Opening dateAugust 15, 1963Closing date1995No. of anchor tenants2No. of floors1 Cobb Center Mall (originally Cobb County Shopping Center) was a shopping mall in Smyrna, Georgia, United States. It was the second mall built in Georgia, and opened on August 15, 1963. Early years The mall was ...

حسن معاذ معلومات شخصية الاسم الكامل حسن معاذ طاهر فلاته الميلاد 27 يناير 1986 (العمر 38 سنة)السعودية الطول 1.73 م (5 قدم 8 بوصة) مركز اللعب ظهير أيمن الجنسية السعودية مسيرة الشباب سنوات فريق 2003–2004 الأنصار المسيرة الاحترافية1 سنوات فريق م. (هـ.) 2004–2017 الشباب 171 (14) 2017–2018 ا�...

GM Europa OviniInformationsStatut Continentale (depuis 2015)Code UCI GMC (2015) et GME (depuis 2016)Discipline Cyclisme sur routePays ItalieCréation 2015Saisons 3Marque de cycles Hersh (depuis 2015)EncadrementDirecteur général Gabriele Marchesani (d) (depuis 2015)Directeurs sportifs Alessandro Spezialetti (2015)Dario Andriotto (depuis 2016)Alessandro Donati (depuis 2016)Dmitri Nikandrov (d) (depuis 2016)Dénominations2015 GMdepuis 2016 GM Europa Ovinimodifier - modifier le code - mod...

On the Jews and Their Lies Title page of Martin Luther's On the Jews and Their LiesAuthorMartin LutherCountryHoly Roman EmpireLanguageGermanSubjectsReligious antisemitism, antisemitic canardGenreReligionPublished1543Original textOn the Jews and Their Lies at Google BooksTranslationOn the Jews and Their Lies at Wikisource Book by Martin Luther On the Jews and Their Lies (German: Von den Jüden und iren Lügen; in modern spelling Von den Juden und ihren Lügen) is a 65,000-word anti-Judaic and ...

Machine used for studying the effects of air moving around objects NASA wind tunnel with the scale model of the MD-11 wide-body airliner 16-foot supersonic wind tunnel at Arnold Air Force Base, 1960 A model Cessna with helium-filled bubbles showing pathlines of the wingtip vortices Wind tunnels are machines where an object is held stationary inside a tube, and air is blown around it to study the interaction between the object and the moving air. They are used to test the aerodynamic effects o...

У этого термина существуют и другие значения, см. Горностай (значения). Горностай Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:Челюстнороты...

تشمل هذه القائمة الأعلام التي تم استخدامها أو التي تستخدمها حاليًا فرنسا والمجموعات الفرنسية لما وراء البحار ومقاطعات وأقاليم ما وراء البحار الفرنسية. علم فرنسا الوطني. العلم الوطني العلم التاريخ الاستعمال الوصف 1790–1794 العلم الوطني في نهاية مملكة فرنسا وبداية الجمهورية �...

1974 film by Kinji Fukasaku New Battles Without Honor and HumanityTheatrical release posterDirected byKinji FukasakuWritten byFumio KonamiMisao AraiProduced byGoro KusakabeStarringBunta SugawaraTomisaburo WakayamaNobuo KanekoKunie TanakaHiroki MatsukataNarrated bySatoshi Tetsu SakaiCinematographySadaji YoshidaEdited byShintaro MiyamotoMusic byToshiaki TsushimaDistributed byToeiRelease date December 28, 1974 (1974-12-28) Running time98 minutesCountryJapanLanguageJapaneseBox offi...
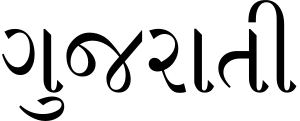
Aksara GujaratJenis aksara Abugida BahasaGujaratSanskertaKutchiAvestanPeriodesekitar 1592–sekarangArah penulisanKiri ke kananAksara terkaitSilsilahAbjad Proto-SinaiAbjad FenisiaAbjad ArameaBrahmiGuptaNāgarīAksara GujaratAksara kerabatRanjanaMoḍīISO 15924ISO 15924Gujr, 320 , GujaratiPengkodean UnicodeNama UnicodeGujaratiRentang UnicodeU+0A80–U+0AFF Artikel ini mengandung transkripsi fonetik dalam Alfabet Fonetik Internasional (IPA). Untuk bantuan dalam memba...

Lauren PotterLauren Potter merayakan upacara pembukaan LA 2015 Special Olympics di Coliseum.Lahir10 Mei 1990 (umur 34)Inland Empire, California, Amerika SerikatPekerjaanPemeran, KomedianTahun aktif2007–sekarang Lauren Elizabeth Potter[1] (lahir 10 Mei 1990) adalah seorang pemeran, advokat, dan komedian Amerika Serikat yang dikenal karena perannya sebagai Becky Jackson dalam seri FOX Glee. Potter mengadvokasi penyandang disabilitas melalui organisasi termasuk AbilityPath, ...

Part of a series onTropical cyclones Structure Central dense overcast Development Eye Effects By Region Warnings and watches Storm surge Preparedness Response Climatology and tracking Basins Climate change effects RSMCs Scales Observation Forecasting Rainfall forecasting Rainfall climatology Tropical cyclone naming History List of historical names Lists of retired names: Atlantic, Pacific hurricane, Pacific typhoon, Philippine, Australian, South Pacific OutlineMedia coverage Tropical cyclone...

لايدي سميث الإحداثيات 48°59′51″N 123°49′13″W / 48.9975°N 123.82027777778°W / 48.9975; -123.82027777778 [1] تاريخ التأسيس 1904 سبب التسمية ليديسميث تقسيم إداري البلد كندا[2][3] خصائص جغرافية المساحة 11.99 كيلومتر مربع ارتفاع 40 متر عدد السكان عدد السك�...

Pandémie de Covid-19 en ÉgypteCarte des gouvernorats avec des cas confirmés (rouges) ou suspectés (bleus) de coronavirus (au 25 mars)Maladie Maladie à coronavirus 2019 (Covid-19)Agent infectieux SARS-CoV-2Origine Wuhan (Hubei, Chine)Localisation ÉgyptePremier cas Le CaireDate d'arrivée Depuis le 14 février 2020 (4 ans, 6 mois et 15 jours)BilanCas confirmés 516 023 (14 janvier 2024)[1]Cas soignés 442 182 (14 janvier 2024)[1]Morts 24 613 (14 janvier 2024)...

King of Aragon and Valencia (1276–85); King of Sicily (1282–85) Peter IIIDetail from the Nuova CronicaKing of Aragon and ValenciaCount of BarcelonaReign27 July 1276 (1276-07-27) – November 1285 (1285-11)PredecessorJames ISuccessorAlfonso IIIKing of Sicily (jure uxoris)Reign4 September 1282 (1282-09-04) – November 1285 (1285-11)PredecessorCharles ISuccessorJames ICo-rulerConstance II of SicilyBornc. 1239Valencia, AragonDiedNovembe...












































