−1 (angka)

−1, terutama dalam matematika, merupakan invers aditif dari bilangan 1, yaitu, suatu bilangan yang bila ditambahkan ke bilangan 1 menghasilkan hasil penjumlahan elemen identitas, atau bilangan 0 ("nol"). Merupakan suatu bilangan bulat negatif yang lebih besar daripada minus dua (−2) dan lebih kecil dari 0.

Bilangan minus satu mempunyai relasi terhadap identitas Euler karena $e^{i\pi }=-1.\!$

Dalam sains komputer, −1 merupakan nilai awal umum untuk "integer" dan juga menunjukkan bahwa suatu variabel tidak memuat informasi yang berguna.

Negatif satu mempunyai sifat-sifat yang mirip tetapi agak berbeda dengan "positif satu".^[1]

Sifat aljabar

Perkalian suatu bilangan dengan −1 ekuivalen dengan mengganti tanda bilangan itu. Ini dapat dibuktikan dengan hukum distribusi dan aksioma bahwa 1 merupakan identitas multiplikatif: untuk bilangan real x, didapatkan

x+(-1)\cdot x=1\cdot x+(-1)\cdot x=(1+(-1))\cdot x=0\cdot x=0

di maan setiap bilangan real x dikalikan 0 sama dengan 0, menyiratkan pembatalan (cancellation) persamaan

0\cdot x=(0+0)\cdot x=0\cdot x+0\cdot x\,

0, 1, −1, i, dan −i dalam bidang kompleks atau Kartesius

Dengan kata lain,

x+(-1)\cdot x=0\,

sehingga (−1) · x merupakan invers aritmetika dari x, atau −x.

Kuadrat dari −1

Kuadrat dari −1, yaitu −1 kali −1, sama dengan 1. Akibatnya, produk dua bilangan real negatif adalah bilangan positif.

Bukti aljabar dari hasil ini dapat diberikan pertama-tama dengan persamaan

0=-1\cdot 0=-1\cdot [1+(-1)]

Persamaan pertama mengikuti hasil di atas. Yang kedua mengikuti definisi −1 sebagai invers aditif dari 1: tepatnya bilangan yang jika ditambahkan ke 1 menghasilkan 0. Menggunakan hukum distributif didapatkan

0=-1\cdot [1+(-1)]=-1\cdot 1+(-1)\cdot (-1)=-1+(-1)\cdot (-1)

Persamaan kedua mengikuti fakta bahwa 1 merupakan identitas multiplikatif. Penambahan 1 ke kedua sisi persamaan terakhir menyiratkan

(-1)\cdot (-1)=1

Argument di atas berlaku pada semua cincin, suatu konsep aljabar abstrak yang mengeneralisasi bilangan bulat dan bilangan real.

Akar kuadrat dari −1

Bilangan kompleks i memenuhi i² = −1, dan sedemikian rupa dapat dianggap sebagai akar kuadrat dari −1. Bilangan kompleks x lain yang memenuhi persamaan x² = −1 hanya −i.^[2] Dalam aljabar kuaternion, yang memuat bidang kompleks, persamaan x² = −1 mempunyai pemecahan tak terhinggal.

Pemangkatan ke bilangan bulat negatif

Pemangkatan ke bilangan real bukan nol dapat dikembangkan ke bilangan bulat negatif. Dibuat definisi bahwa x⁻¹ = 1/x, artinya didefinisikan bahwa pemangkatan suatu bilangan dengan pangkat −1 mempunyai efek yang sama dengan menghitung resiprokal. Definisi ini yang kemudian dikembangkan ke bilangan-bilangan bulat negatif melestarikan hukum eksponensial x^ax^b = x^{(a + b)} untuk bilangan-bilangan real a,b.

Referensi

^ Mathematical analysis and applications By Jayant V. Deshpande, ISBN 978-1-84265-189-6
^ "Ask Dr. Math". Math Forum. Diakses tanggal 2012-10-14.

Read other articles:

Bandar Udara Memanbetsu

Bandar Udara Memanbetsu女満別空港女満別空港Memanbetsu KūkōTerminal penumpang Bandar Udara Memanbetsu (2011)IATA: MMBICAO: RJCMInformasiJenisPublikPengelolaPemerintah JepangLokasiŌzora, JepangKetinggian dpl mdplSitus webmmb-airport.co.jpPetaRJCMLokasi bandar udara di JepangLandasan pacu Arah Panjang Permukaan m kaki 18/36 2.500 8.202 Aspal beton Bandar Udara Memanbetsu (女満別空港code: ja is deprecated , Memanbetsu Kūkō) (IATA: MMB, ICAO: RJCM)[2] mer...

Inter Miami CF

Inter Miami CFNama lengkapClub Internacional de Fútbol MiamiJulukanThe HeronsVice City(El) InterNama singkatInter MiamiBerdiri2020; 4 tahun lalu (2020)PemilikDavid BeckhamJorge MasJose MasPresidenDavid BeckhamKepala pelatihGerardo MartinoLigaMajor League Soccer2023Eastern Conference: 14thOverall: 27thPlayoffs: Did not qualifySitus webSitus web resmi klub Kostum kandang Kostum tandang Musim ini Club Internacional de Fútbol Miami, dikenal dalam bahasa Inggris sebagai Inter Miami CF ...

Scandalo della telefonata

Il cosiddetto scandalo della telefonata riguardò un illecito sportivo commesso durante il campionato di calcio di serie A 1973-74 e che vide coinvolte, con vari ruoli, le società di Foggia e Verona (come direttamente implicate) e Sampdoria (come società danneggiata), nonché il calciatore italo-brasiliano Sergio Clerici e l'arbitro Gino Menicucci, della sezione di Firenze[1]. A seguito di tale vicenda il Verona fu retrocesso in serie B 1974-75, con ripescaggio in serie A della Samp...

Gelang

Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber: Gelang – berita · surat kabar · buku · cendekiawan · JSTOR Gelang emas, atribut kepala suku Batak Karo. Gelang adalah sebuah perhiasan melingkar yang diselipkan atau dikaitkan pada pergelangan tangan ses...

Estrogenic substances

Estrogen medication Not to be confused with Estrogen (medication) or Estrone (medication). Estrogenic substancesEstrone, a major ingredient in estrogenic substancesCombination ofEstroneEstrogen17β-EstradiolEstrogenEquilinEstrogenClinical dataTrade namesAmniotin, Estrogenic Hormones, Estrogenic Substances, Estrolin, Estromone, Folestrin, Follacro, Menformon, Oestroform, Ova-Estrin, Theelestrin, othersOther namesNatural estrogens; Estrone-like preparationsRoutes ofadministrationBy mouth (table...

France 3 Champagne-Ardenne

France 3Champagne-ArdenneCaractéristiquesCréation 25 février 1965Disparition 1er janvier 2017 (disparition informelle)Propriétaire France TélévisionsSlogan « Sur France 3, vous êtes au bon endroit »Format d'image 16/9, 576i (SD), 1080i (HD)Langue FrançaisPays FranceStatut Généraliste régionale publiqueSiège social ReimsAncien nom Télé Lorraine-Champagne (1965-1975)FR3 Lorraine Champagne-Ardenne (1975-1992)France 3 Lorraine Champagne-Ardenne (1992-2010)Site web https...

Mafia state

State system where government is tied with organized crime This article is about systemic corruption of a government by organised crime syndicates. For the 2011 book about Russia, see Mafia State (book). For the greater connotation that literally means rule by thieves, see Kleptocracy. Political corruption Forms and concepts Bribery Cronyism Economics of corruption Electoral fraud Elite capture Influence peddling Kleptocracy Mafia state Nepotism Pyrrhic defeat theory Slush fund Simony State c...

أبر كالسكاغ

أبر كالسكاغ الإحداثيات 61°32′15″N 160°18′58″W / 61.53744°N 160.31607°W / 61.53744; -160.31607 [1] تاريخ التأسيس 13 فبراير 1975 تقسيم إداري البلد الولايات المتحدة[2] خصائص جغرافية المساحة 10.700079 كيلومتر مربع10.700078 كيلومتر مربع (1 أبريل 2010)[3] ارتفاع 12 متر عدد...

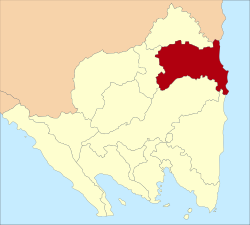
Daftar kecamatan dan kelurahan di Kabupaten Tulang Bawang

Peta Lokasi Kabupaten Tulang Bawang di Lampung Berikut ini adalah daftar kecamatan dan kelurahan/desa di kabupaten Tulang Bawang, Provinsi Lampung, Indonesia. Kabupaten Tulang Bawang terdiri dari 15 kecamatan, 4 kelurahan, dan 147 desa. Pada tahun 2021, jumlah penduduknya mencapai 430,630 jiwa dengan luas wilayah 3.466,32 km² dan sebaran penduduk 124 jiwa/km².[1][2] Daftar kecamatan dan kelurahan di Kabupaten Tulang Bawang, adalah sebagai berikut: Kode Kemendagri Kecamatan J...

土库曼斯坦总统

土库曼斯坦总统土库曼斯坦国徽土库曼斯坦总统旗現任谢尔达尔·别尔德穆哈梅多夫自2022年3月19日官邸阿什哈巴德总统府（Oguzkhan Presidential Palace）機關所在地阿什哈巴德任命者直接选举任期7年，可连选连任首任萨帕尔穆拉特·尼亚佐夫设立1991年10月27日土库曼斯坦土库曼斯坦政府与政治国家政府土库曼斯坦宪法国旗国徽国歌立法機關（英语：National Council of Turkmenistan） ...

Daftar Presiden Togo

Presiden theRepublik TogoPrésident de laRépublique togolaisePetahanaFaure Gnassingbésejak 4 Mei 2005KediamanIstana Gubernur, LoméMasa jabatan5 tahunPejabat perdanaSylvanus OlympioDibentuk27 April 1960 Berikut adalah daftar Presiden Togo sejak pembentukan jabatan Presiden pada 27 April 1960 hingga saat ini. Daftar Presiden Partai politik Komite Persatuan Togo (CUT) Gerakan Rakyat Togo (MPT) Rapat Umum Rakyat Togo (RPT) Persatuan Republik...

Romana

Romana RumànaKomuneComune di RomanaLokasi Romana di Provinsi SassariNegaraItaliaWilayah SardiniaProvinsiSassari (SS)Pemerintahan • Wali kotaLucia CatteLuas • Total21,60 km2 (8,34 sq mi)Ketinggian267 m (876 ft)Populasi (2016) • Total543[1]Zona waktuUTC+1 (CET) • Musim panas (DST)UTC+2 (CEST)Kode pos07010Kode area telepon079Situs webhttp://www.comune.romana.ss.it Romana (bahasa Sardinia: Rumàna) adalah sebua...

يورقون أباد سفلي

يورقون أباد سفلي تقسيم إداري البلد إيران [1] إحداثيات 37°40′52″N 45°08′51″E / 37.6811°N 45.1475°E / 37.6811; 45.1475 الرمز الجغرافي 18490 تعديل مصدري - تعديل يورقون‌ أباد سفلي هي قرية في مقاطعة أرومية، إيران. عدد سكان هذه القرية هو 195 في سنة 2006.[2] مراجع ^ صفحة ي...

Mitsusuke Harada

Japanese master of Shotokai karate (1928–2021) Mitsusuke HaradaBorn(1928-11-16)16 November 1928Dairen, Manchuria, Empire of JapanDied26 February 2021(2021-02-26) (aged 92)Cwmbran, Wales, United KingdomStyleShotokai karateTeacher(s)Shigeru Egami, Gichin Funakoshi, Gigō Funakoshi, Genshin HironishiRank5th dan karateWebsitehttp://www.karatedoshotokai.com/ Mitsusuke Harada, MBE (原田満祐, Harada Mitsusuke, 16 November 1928 – 26 February 2021) was a prominent Japanese master of Shot...

Бєлінський Віссаріон Григорович

Бєлінський Віссаріон ГригоровичБелинский Виссарион Григорьевич Ім'я при народженні Бѣлинскій Виссаріон ГригорьевичъНародився 30 травня (11 червня) 1811[1][2][…]Свеаборг, Велике князівство Фінляндське, Російська імперія[4][1][…]Помер 26 травня (7 червня) 1848[1]...

District of Columbia Organic Act of 1801

1801 U.S. Congress statute which formally placed the District of Columbia under its control For the subsequent act creating a unified government for the whole district, see District of Columbia Organic Act of 1871. The District of Columbia Organic Act of 1801, officially An Act Concerning the District of Columbia (6th Congress, 2nd Sess., ch. 15, 2 Stat. 103, February 27, 1801), is an organic act enacted by the United States Congress in accordance with Article 1, Section 8 of the Un...

Seilbahn Rigiblick

Seilbahn Rigiblick Beide Wagen an der Kreuzungstation Hadlaubstrasse Seilbahn Rigiblick Streckennummer:ZVV Linie 23Fahrplanfeld:2701 (früher 1701)Spurweite:1000 mm (Meterspur)Maximale Neigung: 360 ‰ Legende Zürich, Seilbahn Rigiblick 493 m ü. M. Zürich, Goldauerstrasse 517 m ü. M. Zürich, Hadlaubstrasse (Ausweichstelle) 540 m ü. M. Zürich, Germaniastrasse 565 m ü. M. Zürich, Rigiblick 580 m ü. M....

Boom! (film)

1968 film by Josph Losey This article is about the 1968 British drama film. For the 2004 Bollywood film, see Boom (film). Boom!Theatrical release posterDirected byJoseph LoseyScreenplay byTennessee WilliamsBased onThe Milk Train Doesn't Stop Here Anymoreby Tennessee WilliamsProduced byJohn HeymanStarring Elizabeth Taylor Richard Burton Noël Coward CinematographyDouglas SlocombeEdited byReginald BeckMusic byJohn BarryColor processTechnicolorProductioncompanies World Film Services Moon Lake Jo...

Ellen Clark Sargent

Ellen Clark SargentBornEllen Clark1826 (1826)MassachusettsDiedJuly 13, 1911(1911-07-13) (aged 84–85)San Francisco, CaliforniaNationalityAmericanSpouse Aaron Augustus Sargent (m. 1852⁠–⁠1887) his death Ellen Clark Sargent (Massachusetts, 1826–1911) was an active American women's suffragist. She was influential in advocacy for the Nineteenth Amendment to the United States Constitution, which sought to give women the right ...

2024 Austin mayoral election

2024 Austin mayoral election ← 2022 November 5, 2024 2028 → Incumbent Mayor Kirk Watson Elections in Texas Federal government Presidential elections 1848 1852 1856 1860 1872 1876 1880 1884 1888 1892 1896 1900 1904 1908 1912 1916 1920 1924 1928 1932 1936 1940 1944 1948 1952 1956 1960 1964 1968 1972 1976 1980 1984 1988 1992 1996 2000 2004 2008 2012 2016 2020 2024 Presidential primaries Democratic 2000 2004 2008 2012 2016 2020 2024 Republican 1996 2000 2004 2008 2012 2016 ...