Általánosított inverz eloszlásfüggvény
|
Read other articles:

The CodeAlbum mini karya Monsta XDirilis07 November 2017 (2017-11-07)GenreK-pophip hopBahasaKoreaLabelStarship EntertainmentLOEN EntertainmentKronologi Monsta X The Clan Pt. 2.5: The Final Chapter(2017) The Code(2017) The Connect: Dejavu(2018) Singel dalam album The Code DramaramaDirilis: 7 November 2017 The Code adalah album mini kelima dari boy band asal Korea Selatan Monsta X. Album mini ini dirilis pada tanggal 7 November 2017, oleh Starship Entertainment. Album ini terdiri dari ...

American physician (born 1949) Peter AgreBorn (1949-01-30) January 30, 1949 (age 75)Northfield, Minnesota, U.S.Alma materAugsburg College (BA)Johns Hopkins University (MD)Known forAquaporinsAwardsNobel Prize in Chemistry (2003) Bloomberg Distinguished Professorships (2014)Scientific careerFieldsMedicineChemistryBiochemistryInstitutionsJohns Hopkins Malaria Research Institute Duke University Case Western Reserve Peter Agre (/ˈɑːɡriː/; born January 30, 1949) is an American p...

Artikel ini perlu diwikifikasi agar memenuhi standar kualitas Wikipedia. Anda dapat memberikan bantuan berupa penambahan pranala dalam, atau dengan merapikan tata letak dari artikel ini. Untuk keterangan lebih lanjut, klik [tampil] di bagian kanan. Mengganti markah HTML dengan markah wiki bila dimungkinkan. Tambahkan pranala wiki. Bila dirasa perlu, buatlah pautan ke artikel wiki lainnya dengan cara menambahkan [[ dan ]] pada kata yang bersangkutan (lihat WP:LINK untuk keterangan lebih lanjut...

Prostate cancer treatment BicalutamideClinical dataPronunciationBicalutamide:• /ˌbaɪkəˈluːtəmaɪd/[1]• BY-kə-LOO-tə-myde[1] Trade namesCasodex, Calutex, othersOther namesICI-176,334; ZD-176,334AHFS/Drugs.comMonographMedlinePlusa697047License data US DailyMed: Bicalutamide US FDA: Bicalutamide Pregnancycategory AU: D Routes ofadministrationBy mouth[2]Drug classNonsteroidal antiandrogenATC codeL02BB03 (WHO) Legal status...

Kongres Nasional Partai Komunis Tiongkok ke-11 diselenggarakan pada 12-18 Agustus 1977, sekitar lima tahun sebelum Kongres Nasional ke-12 dan empat tahun setelah Kongres Nasional ke-10. Kongres ini secara resmi mendeklarasikan bahwa Revolusi Kebudayaan telah berakhir setelah berlangsung selama 11 tahun, mengakhiri babak panjang sejarah Tiongkok. Kelompok Empat sepenuhnya dikritik karena peran mereka dalam Revolusi Kebudayaan. Hua Guofeng secara resmi terpilih sebagai Ketua Komite Sentral ke-1...

كتلة سوداء في مسيرة فرعية بالقرب من البنك الدولي في واشنطن العاصمة في عام 2009. لاحظ أن بعض المتظاهري الكتلة السوداء قد يرتدون اغطية الرأس ببساطة، مما يسمح بعرض وجوههم، والبعض الآخر قد يستخدم أشياء مثل الوشاح والنظارات الشمسية الداكنة أو أقنعة لإخفاء وجوههم قدر الأمكان. بلا�...

Homeless advocacy group and newspaper in Portland, Oregon, United States Street RootsA Street Roots salesman with newspapersTypeWeekly alternative newspaperFormatCompactEditorK. Rambo [1]Founded1998 [2]Political alignmentHomeless advocacyHeadquartersPortland, Oregon, U.S.Circulation10,000 (as of 2018)[3]Websitestreetroots.org Street Roots is a Portland, Oregon, United States based homeless advocacy group[4] and a weekly alternative newspaper that covers hom...
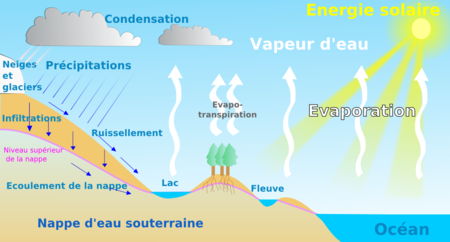
Ne doit pas être confondu avec Petit cycle de l'eau. Cycle de l'eauSchéma du cycle de l'eau.PrésentationPartie de Hydrologiemodifier - modifier le code - modifier Wikidata Le cycle de l'eau, ou cycle hydrologique correspond à l'ensemble des transferts d'eau (liquide (eau du robinet), solide (grêle )ou gazeuse (vapeur d'eau)) entre les réservoirs d'eau sur Terre (les océans, l'atmosphère, les lacs, les cours d'eau, les nappes d'eau souterraine et les glaciers). Le « moteur ...

Eccellenza 2010-2011 Competizione Eccellenza Sport Calcio Edizione 20ª Organizzatore Lega Nazionale Dilettanti Luogo Italia Partecipanti 477 Formula 28 gironi all'italiana Cronologia della competizione 2009-2010 2011-2012 Manuale Il campionato italiano di calcio di Eccellenza 2010-2011 è il sesto livello del campionato italiano di calcio per la stagione 2010-2011 ed il primo livello regionale. È costituito da 28 gironi gestiti direttamente dai Comitati Regionali della Lega Nazionale...

Goodluck Jonathan Presiden Nigeria ke-14Masa jabatan5 Mei 2010 – 29 Mei 2015Wakil PresidenNamadi SamboPendahuluUmaru Yar'AduaPenggantiMuhammadu BuhariWakil Presiden NigeriaMasa jabatan29 Mei 2007 – 5 Mei 2010PresidenUmaru Yar'AduaPendahuluAtiku AbubakarPenggantiPetahanaGubernur BayelsaMasa jabatan9 Desember 2005 – 28 Mei 2007PendahuluDiepreye AlamieyeseighaPenggantiTimipre Sylva Informasi pribadiLahir20 November 1957 (umur 66)Ogbia, NigeriaPartai politikP...

本條目存在以下問題,請協助改善本條目或在討論頁針對議題發表看法。 此條目需要編修,以確保文法、用詞、语气、格式、標點等使用恰当。 (2013年8月6日)請按照校對指引,幫助编辑這個條目。(幫助、討論) 此條目剧情、虛構用語或人物介紹过长过细,需清理无关故事主轴的细节、用語和角色介紹。 (2020年10月6日)劇情、用語和人物介紹都只是用於了解故事主軸,輔助�...

Les problèmes du prix du millénaire sont un ensemble de sept défis mathématiques réputés insurmontables, posés par l'Institut de mathématiques Clay en 2000. La résolution de chacun des problèmes est dotée d'un prix d'un million de dollars américains offert par l'institut Clay. En 2024, six des sept problèmes demeurent non résolus. Description générale Chacun des défis consiste à : soit démontrer, soit infirmer, une hypothèse ou une conjecture qui n'a été ni confirm�...

Starting point of a river Headwater redirects here. For other uses, see Headwater (disambiguation). This article is about the heads of rivers. For the insurance company, see RiverSource. River Wey near its source at Farringdon The headwater of a river or stream is the farthest point on each of its tributaries upstream from its mouth/estuary into a lake/sea or its confluence with another river. Each headwater is considered one of the river's sources, as it is the place where surface runoffs fr...

For the suburb within the City of York, see Acomb, North Yorkshire. Human settlement in EnglandAcombAcomb rooftopsAcombLocation within NorthumberlandPopulation1,184 (2001 census)[1]OS grid referenceNY931664Unitary authorityNorthumberlandCeremonial countyNorthumberlandRegionNorth EastCountryEnglandSovereign stateUnited KingdomPost townHEXHAMPostcode districtNE46Dialling code01434PoliceNorthumbriaFireNorthumberlandAmbulanceNorth East UK Parli...

Scottish writer Johann HariHari in 2011BornJohann Eduard Hari (1979-01-21) 21 January 1979 (age 45)Glasgow, ScotlandCitizenship United Kingdom Switzerland Alma materKing's College, CambridgeOccupationWriterNotable workChasing the ScreamWebsitejohannhari.com Johann Eduard Hari (born 21 January 1979) is a Scottish writer and journalist who wrote for The Independent and The Huffington Post. In 2011, Hari was suspended from The Independent and later resigned, after admitting to plagiari...

Kamis HitamNilai grafik Dow Jones mencapai tertinggi sepanjang masa pada Februari 2020, dan kemudian jatuh pada akhir Februari hingga Maret 2020.Tanggal12 Maret 2020JenisPenurunan pasar sahamPenyebab Pandemi COVID-19–ketidakstabilan pasar yang disebabkan oleh pandemi Pelarangan perjalanan warga negara Amerika Serikat ke Kawasan Schengen Keputusan Bank Sentral Eropa untuk tidak memotong suku bunga Kamis Hitam adalah penurunan pasar saham global pada 12 Maret 2020, sebagai bagian dari penurun...

Archivio centrale dello Stato Sede dell'Archivio Centrale dello Stato SiglaACS Stato Italia Tipoarchivio Istituito1875 PredecessoreArchivio del Regno SovrintendenteAndrea De Pasquale SedeRoma IndirizzoPiazzale degli Archivi, 27 (EUR) Sito webacs.cultura.gov.it/ Modifica dati su Wikidata · Manuale Archivio Centrale dello StatoUbicazioneStato Italia CittàRoma IndirizzoPiazzale degli Archivi, 27, 00144 Roma e Piazzale degli Archivi, 27 - Roma Dati generaliTipologia funzionalearc...

Pietro Scaglione Pietro Scaglione (Lercara Friddi, 2 marzo 1906 – Palermo, 5 maggio 1971) è stato un magistrato italiano, assassinato da Cosa nostra[1]. Con decreto del Ministero della Giustizia del 1991, previo parere favorevole del Consiglio Superiore della Magistratura, Pietro Scaglione fu riconosciuto magistrato caduto vittima del dovere e della mafia[2]. È sepolto nel Cimitero dei Cappuccini di Palermo. Indice 1 Biografia 1.1 L'ingresso e la carriera nella magistratur...

Velodromo Paolo Borsellino Informazioni generaliStato Italia UbicazioneVia Giuseppe Lanza di ScaleaPalermo Inizio lavori1989 Inaugurazione2 febbraio 1991 ProprietarioComune di Palermo ProgettoRocco Abbate Prog. strutturaleMaurizio Arici Intitolato aPaolo Borsellino Informazioni tecnichePosti a sedere12 000 Strutturapianta ovale Coperturalignea sulla sola tribuna Mat. del terrenoErba Dim. del terreno100x60 m Uso e beneficiariFootball americano Sharks Palermo Cardinals Paler...

Yosua 9Kitab Yosua lengkap pada Kodeks Leningrad, dibuat tahun 1008.KitabKitab YosuaKategoriNevi'imBagian Alkitab KristenPerjanjian LamaUrutan dalamKitab Kristen6← pasal 8 pasal 10 → Yosua 9 (disingkat Yos 9) adalah pasal kesembilan Kitab Yosua dalam Alkitab Ibrani dan Perjanjian Lama di Alkitab Kristen yang memuat riwayat Yosua dalam memimpin orang Israel menduduki tanah Kanaan.[1] Pasal ini berisi riwayat akal orang Gibeon supaya tidak dimusnahkan oleh orang Israel.[...
























