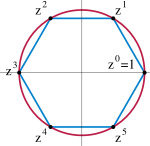
Normálosztó
|
Read other articles:

The State of Kerala consist of 14 districts, 27 revenue divisions, and 78 taluks. Each revenue division is headed by a Revenue Divisional Officer, who is also the Sub-divisional Magistrate and assisted by Senior Superintendent among others.[1] Administrative map of Kerala Kasaragod District Kasaragod RDO: Manjeshwaram (HQ: Uppala), Kasaragod Kanhangad RDO: Vellarikundu, Hosdurg (HQ: Kanhangad) Kannur District Taliparamba RDO: Payyanur, Taliparamba, Kannur Thalassery RDO: Thalassery, ...

Georg Maria StenzGeorg Maria StenzLahir22 November 1869Horhausen, WesterwaldMeninggal23 April 1928 (umur 58)Techny, Illinois, Amerika SerikatKebangsaanJermanNama lainHanzi: 薛田资; Pinyin: Xuē TiánzīPekerjaanMisionaris di Shandong, TiongkokTahun aktif1893 hingga 1927OrganisasiSerikat Sabda AllahDikenal atasInsiden Juye, Insiden JietouTanda tangan Georg Maria Stenz (Hanzi: 薛田资; Pinyin: Xuē Tiánzī, 22 November 1869[1] – 23 April 1928[2]...
Him LawNama Tionghoa羅仲謙 (Tradisional)Nama Tionghoa罗仲谦 (Sederhana)PinyinLuó Zhòngqiān (Mandarin)JyutpingLo4 Zung6 Him1 (Kanton)PekerjaanAktorTahun aktif2005–sekarangPasanganTavia YeungPartnerTheresa Fu (2010-2011) Law Chung-him (lahir 28 Agustus 1984) dikenal juga sebagai Him Law adalah aktor film dan televisi asal Hongkong. Filmografi Film Judul Tahun Peran Catatan Mob Sister 2005 Little Red Cap Black Night 2006 Segment: Next Door Eye in the Sky 2007 policeman Kidnap 2007 Fat...

Music startup based in San Francisco, California BandPageType of siteTools & Application For MusiciansFoundedSeptember 2009; 14 years ago (2009-09)HeadquartersSan Francisco, California, United StatesOwnerGoogleLaunchedMarch 2010Current statusInactive BandPage was a music startup based in San Francisco, California that produced the application BandPage, which powered over 500,000 artists' Facebook Pages.[1] Artists could upload and share tracks, videos, ...

Assassinat de Samuel Paty Fleurs déposées devant le collège du Bois-d'Aulne, à Conflans-Sainte-Honorine, en hommage à Samuel Paty. Localisation 39-41, rue du Buisson-Moineau, Éragny-sur-Oise, Val-d'Oise, France[1] Cible Samuel Paty Coordonnées 49° 00′ 50″ nord, 2° 06′ 54″ est Date 16 octobre 2020 16 h 52[2] (HAEC) Type AssassinatDécapitation Armes Couteauxpistolet airsoft Morts 2 (Samuel Paty et le terroriste) Auteurs Abdoullakh Anzor...

Nama ini menggunakan cara penamaan Spanyol: nama keluarga pertama atau paternalnya adalah Sánchez dan nama keluarga kedua atau maternalnya adalah Moreno. Carlos Sánchez Informasi pribadiNama lengkap Carlos Alberto Sánchez MorenoTanggal lahir 6 Februari 1986 (umur 38)Tempat lahir Quibdó, KolombiaTinggi 1,82 m (5 ft 11+1⁄2 in)[1]Posisi bermain GelandangInformasi klubKlub saat ini Fiorentina (pinjaman dari Aston Villa)Nomor 6Karier junior2003–2005 Dan...

French engineer Philippe-Jean Bunau-VarillaPhilippe-Jean Bunau-Varilla in 1924Personal detailsBorn(1859-07-26)26 July 1859Paris, French EmpireDied18 May 1940(1940-05-18) (aged 80)Paris, FranceNationalityFrenchKnown forPanama Canal Philippe-Jean Bunau-Varilla (French: [filip ʒɑ̃ byno vaʁija]; 26 July 1859 – 18 May 1940) was a French engineer and soldier. With the assistance of American lobbyist and lawyer William Nelson Cromwell, Bunau-Varilla greatly influenced Washingt...

Zakharia 13Sebagian Kitab Zakharia pada Codex Gigas, yang dibuat sekitar abad ke-13.KitabKitab ZakhariaKategoriNabi-nabi KecilBagian Alkitab KristenPerjanjian LamaUrutan dalamKitab Kristen38← pasal 12 pasal 14 → Zakharia 13 (disingkat Zak 13) adalah bagian dari Kitab Zakharia dalam Alkitab Ibrani dan Perjanjian Lama di Alkitab Kristen. Memuat Firman Allah yang disampaikan dengan perantaraan nabi Zakharia.[1][2] Teks Naskah aslinya ditulis dalam bahasa Ibrani. Pasal...

This article is about the video game. For the Japanese military operation on Ceylon and the Indian ocean, see Indian Ocean raid (1942). This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Operation C video game – news · newspapers · books · scholar · JSTOR (April 2022) (Learn how and when to remove this tem...

Сибирский горный козёл Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:СинапсидыКла�...

4th race of the 2023 NASCAR Xfinity Series 2023 United Rentals 200 Race details Race 4 of 33 of the 2023 NASCAR Xfinity Series Date March 11, 2023Official name 19th Annual United Rentals 200Location Phoenix Raceway, Avondale, ArizonaCourse Permanent racing facility1 mi (1.6 km)Distance 200 laps, 200 mi (320 km)Scheduled Distance 200 laps, 200 mi (320 km)Average speed 82.079 mph (132.093 km/h)Pole positionDriver Cole Custer Stewart-Haas RacingTime 27.701Most laps ledDriver Sammy Smit...

Congolese footballer Delvin N'Dinga N'Dinga with Lokomotiv in 2016Personal informationFull name Delvin Chanel N'Dinga[1]Date of birth (1988-03-14) 14 March 1988 (age 36)Place of birth Pointe Noire, Republic of the CongoHeight 1.81 m (5 ft 11+1⁄2 in)Position(s) MidfielderYouth career2002 CNFF2003–2005 Diables NoirsSenior career*Years Team Apps (Gls)2005–2008 Auxerre B 57 (3)2008–2012 Auxerre 78 (2)2012–2016 Monaco 27 (0)2013–2015 → Olympiacos (loan...

内華達州 美國联邦州State of Nevada 州旗州徽綽號:產銀之州、起戰之州地图中高亮部分为内華達州坐标:35°N-42°N, 114°W-120°W国家 美國建州前內華達领地加入聯邦1864年10月31日(第36个加入联邦)首府卡森城最大城市拉斯维加斯政府 • 州长(英语:List of Governors of {{{Name}}}]]) • 副州长(英语:List of lieutenant governors of {{{Name}}}]])喬·隆巴爾多(R斯塔...

Sporting event delegationTogo at the2018 Winter OlympicsFlag of TogoIOC codeTOGNOCComité National Olympique Togolaisin Pyeongchang, South KoreaFebruary 9–25, 2018Competitors1 in 1 sportFlag bearer Mathilde-Amivi Petitjean (opening & closing)Medals Gold 0 Silver 0 Bronze 0 Total 0 Winter Olympics appearances (overview)201420182022 Togolese-born skier and former competitor for France Mathilde-Amivi Petitjean competed in cross-country skiing as the only athlete representing Togo. To...

Main cast Cast lists for different versions of The Hitchhiker's Guide to the Galaxy. A blank cell in the table indicates that the information is unknown. N/A indicates that the role in question does not exist for that version of the story. Columns are in chronological order from 1978–2005, except for the two German radio series (1981 and 1990–1991). Character's Name Primary and Secondary Phases[1] Stage Adaptation LP Adaptations[2][3] TV series[4] Illustra...

European immigration to the Americas was one of the largest migratory movements in human history. Between the years 1492 and 1930, more than 60 million Europeans immigrated to the American continent. Between 1492 and 1820, approximately 2.6 million Europeans immigrated to the Americas, of whom just under 50% were British, 40% were Spanish or Portuguese, 6% were Swiss or German, and 5% were French. But it was in the 19th century and in the first half of the 20th century that European imm...

ХуторНововесёлый 46°40′44″ с. ш. 42°50′43″ в. д.HGЯO Страна Россия Субъект Федерации Ростовская область Муниципальный район Зимовниковский Сельское поселение Савоськинское История и география Часовой пояс UTC+3:00 Население Население 186[1] человек (2010) Назва�...

Perceived cardiac abnormality in which one's heartbeat can be felt Not to be confused with palpation. Medical conditionPalpitationArtistic impression of a woman experiencing syncope, which may accompany heart palpitationsSpecialtyCardiologyDifferential diagnosisTachycardia Palpitations are perceived abnormalities of the heartbeat characterized by awareness of cardiac muscle contractions in the chest, which is further characterized by the hard, fast and/or irregular beatings of the heart.[...

Human settlement in ScotlandCairnbaanScottish Gaelic: An Càrn BànCup and ring marks on a stone near CairnbaanCairnbaanLocation within Argyll and ButeOS grid referenceNR830907Council areaArgyll and ButeLieutenancy areaArgyll and ButeCountryScotlandSovereign stateUnited KingdomPost townLOCHGILPHEADPostcode districtPA31PoliceScotlandFireScottishAmbulanceScottish UK ParliamentArgyll and ButeScottish ParliamentArgyll and Bute List of places UK Scotland 56...

Core group of ancient Hebrew scriptures Tanakh redirects here. For other uses, see Tanakh (disambiguation). This article is about the Jewish text. For other uses, see Old Testament, Bible translations into Hebrew, and Hebrew Bible: A Critical Edition. Hebrew Bibleתַּנַ״ךְ, TanakhComplete set of scrolls, constituting the TanakhInformationReligionJudaismChristianityLanguageBiblical HebrewBiblical AramaicPeriod8th/7th centuries BCE – 2nd/1st centuries BCEHebrew Bible at Hebrew W...