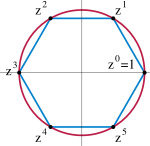
Csoport (matematika)
|
Read other articles:

Stasiun Suzuka鈴鹿駅Stasiun SuzukaLokasi1-11-1 Yabase, Suzuka, Mie(三重県鈴鹿市矢橋一丁目11-1)JepangOperatorIse RailwayJalurJalur IseInformasi lainKode stasiun4SejarahDibuka1973PenumpangFY2010220 per hari Sunting kotak info • L • BBantuan penggunaan templat ini Stasiun Suzuka (鈴鹿駅code: ja is deprecated , Suzuka-eki) adalah sebuah stasiun kereta api di Suzuka, Prefektur Mie, Jepang, yang dioperasikan olehIse Railway. Stasiun tersebut berjarak 3.8 kilometer...

American novel about gambling The Hustler First editionAuthorWalter TevisPublisherHarper & BrothersPublication date1959 The Hustler is a 1959 debut novel by American writer Walter Tevis. It tells the story of a young pool hustler, Edward Fast Eddie Felson, who challenges the legendary Minnesota Fats.[1] The novel was well-received by critics, and was adapted into a 1961 film of the same title, starring Paul Newman as Fast Eddie, Jackie Gleason as Minnesota Fats, and Piper Laurie ...

Reverendus PaterJohannes Maria HämmerleOFM.Cap.Provinsi gerejawiMedanKeuskupanSibolgaImamatTahbisan imam1968; 56 tahun lalu (1968)Informasi pribadiNama lahirMartin Georg HammerleLahir9 Juli 1941 (umur 82)Hausach, Baden-Württemberg, JermanKewarganegaraanIndonesiaDenominasiKatolik RomaPekerjaanImamPenulis R.P. Johannes Maria Hämmerle, OFM.Cap. (lahir 9 Juli 1941) adalah seorang imam Gereja Katolik asal Jerman, misionaris Kapusin di Pulau Nias, budayawan Nias, dan juga penulis. Ia b...

Часть серии статей о Холокосте Идеология и политика Расовая гигиена · Расовый антисемитизм · Нацистская расовая политика · Нюрнбергские расовые законы Шоа Лагеря смерти Белжец · Дахау · Майданек · Малый Тростенец · Маутхаузен ·&...

المجلس الوطني الاتحادي النوع التأسيس 1971 النوع غرفة واحدة البلد الإمارات العربية المتحدة القيادة صقر غباش الأعضاء 40 مكان الاجتماع أبوظبي الموقع الإلكتروني www.almajles.gov.ae تعديل مصدري - تعديل المجلس الوطني الاتحادي يعرف بالسلطة التشريعية للإمارات العربية المتحد...

Zainichi Korean wrestler (born 1980) Ryoji SaiBorn (1980-06-03) June 3, 1980 (age 43)[1]Osaka, Japan[2]Professional wrestling careerRing name(s)Ryoji Sai[1]Billed height6 ft 3 in (1.91 m)[1]Billed weight231 lb (105 kg) [1]Trained byGerard GordeauZero1 DojoDebutSeptember 1, 2001[3] Ryoji Sai[1] (崔領二, Sai Ryōji, 최영이) (born Choi Young-ii June 3, 1980) is a Korean professional wrestler, mixed martia...

هذه مقالة غير مراجعة. ينبغي أن يزال هذا القالب بعد أن يراجعها محرر؛ إذا لزم الأمر فيجب أن توسم المقالة بقوالب الصيانة المناسبة. يمكن أيضاً تقديم طلب لمراجعة المقالة في الصفحة المخصصة لذلك. (أكتوبر 2022) الميثاقمعلومات عامةالنوع الكترونية ورقيةبلد المنشأ اليمنالتأسيس 1982موقع ...

Rektor Universitas BrawijayaPetahanaProf. Dr. Ir. Nuhfil Hanani AR, MSsejak 28 Juni 2018Menjabat selama4 TahunPemegang pertamaDr. Doel ArnowoDibentuk5 Januari 1963Situs webhttps://pilrek.ub.ac.id/ Universitas Brawijaya (UB) sudah memiliki 13 rektor yang menjabat sejak awal pendiriannya pada tahun 1963. Nama Rektor Universitas Brawijaya berubah dari waktu ke waktu sebagai berikut:[1] Presiden Universitas Brawijaya (1963–1966) Ketua Presidium Universitas Brawijaya (1966) Rektor U...

Jacques Maritain Jacques Maritain (Parigi, 18 novembre 1882 – Tolosa, 28 aprile 1973) è stato un filosofo francese, convertitosi al cattolicesimo. Allievo di Henri Bergson, fu autore di più di sessanta opere ed è generalmente considerato come uno dei massimi esponenti del neotomismo nei primi decenni del XX secolo, nonché uno tra i più grandi pensatori cattolici del secolo. Fu anche il filosofo che più di ogni altro avvicinò gli intellettuali cattolici alla democrazia allontanandoli ...

Russian school subject Visual identity of Conversations about Important Things.[1] Conversations about Important Things[2] (Russian: Разговоры о важном, romanized: Razgovory o vazhnom, lit. 'Conversations about that which is important'), or Important Conversations for short,[3] is a name for a series of compulsory school lessons in Russia that covers various topics from the Russian government's perspective, such as national identity, public h...

Chemical compound GuanoclorClinical dataATC codeC02CC05 (WHO) Identifiers IUPAC name 2-{[2-(2,6-Dichlorophenoxy)ethyl]amino}guanidine CAS Number5001-32-1PubChem CID71835ChemSpider64857UNIIM4HBT852YOCompTox Dashboard (EPA)DTXSID10198184 ECHA InfoCard100.023.334 Chemical and physical dataFormulaC9H12Cl2N4OMolar mass263.12 g·mol−13D model (JSmol)Interactive image SMILES C1=CC(=C(C(=C1)Cl)OCCNNC(=N)N)Cl InChI InChI=1S/C9H12Cl2N4O/c10-6-2-1-3-7(11)8(6)16-5-4-14-15-9(12)13/h1-3,14...

State agency of Kentucky This article may rely excessively on sources too closely associated with the subject, potentially preventing the article from being verifiable and neutral. Please help improve it by replacing them with more appropriate citations to reliable, independent, third-party sources. (June 2022) (Learn how and when to remove this message) The Kentucky Department of Juvenile Justice (KYDJJ) is a state agency of Kentucky headquartered in unincorporated Franklin County, near Fran...

British thriller series This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article possibly contains original research. Please improve it by verifying the claims made and adding inline citations. Statements consisting only of original research should be removed. (August 2023) (Learn how and when to remove this message) This article needs additional citations for verification. Please hel...

Italian stew CiambottaAlternative namesCiambotta, giambotta, ciambrotta, ciammotta, cianfotta, ciabottaTypeStewCourseSide dish or entréePlace of originItalyRegion or stateSouthern ItalyMain ingredientsVegetables Ciambotta or giambotta is a summer vegetable stew of southern Italian cuisine. The dish has different regional spellings;[1][2] it is known as ciambotta or ciambrotta in Calabria and elsewhere,[2][3] ciammotta in Basilicata[3] and Calabria,[...

International trademark registration system Madrid Agreement redirects here. For other uses, see Madrid Agreement (disambiguation). For the Madrid Protocol relating to mining in the Antarctic, see Protocol on Environmental Protection to the Antarctic Treaty. For the great-power agreement over the Sulu Archipelago, see Madrid Protocol of 1885. This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages...

American educator, artist and researcher (1961–2020) Michael HawleyMichael Hawley in Siem Reap 2002Born(1961-11-18)November 18, 1961Camp Pendleton, California, U.S.DiedJune 24, 2020(2020-06-24) (aged 58)Cambridge, Massachusetts, U.S.Alma materYale University, Massachusetts Institute of TechnologySpouseNina YouChildren1AwardsTetelman Fellow, Van Cliburn competition, Kilby International AwardsScientific careerFieldsComputer ScienceDoctoral advisorMarvin Minsky Michael Jerome Hawley...

Vorobyovy GoryStasiun Metro MoskwaLokasiRussiaPemilikMoskovsky MetropolitenJalur!C 1 Jalur Sokolnicheskaya Jumlah peron1 peron pulauJumlah jalur2KonstruksiTinggi peron1ParkirTidak adaFasilitas sepedaTidak adaInformasi lainKode stasiun016SejarahDibuka1 Desember 1959; 64 tahun lalu (1959-12-01)Dibangun kembali20 Oktober 1983; 40 tahun lalu (1983-10-20) to 14 Desember 2002; 21 tahun lalu (2002-12-14)Nama sebelumnyaLeninskye GoryOperasi layanan Stasiun sebelum...

Australian morning tabloid newspaper Northern Territory NewsTypeDaily newspaperFormatTabloidOwner(s)News Corp AustraliaFounder(s)Don Whitington, Eric White & John ColemanEditorMelanie PlaneFounded8 February 1952Political alignmentCentre-right[1] or syncretic[2][3]HeadquartersPrinters Place Darwin, Northern TerritorySister newspapersCentralian Advocate (online only)ISSN1837-3909OCLC number1126462895 Websitentnews.com.au The Northern Territory News (also known and br...

American college basketball season 2015–16 North Carolina Central Eagles men's basketballConferenceMid-Eastern Athletic ConferenceRecord13–19 (7–9 MEAC)Head coachLeVelle Moton (7th season)Assistant coaches Chris Skinkis Chuck Taylor Eric Wilson Home arenaMcLendon–McDougald GymnasiumSeasons← 2014–152016–17 → 2015–16 MEAC men's basketball standings vte Conf Overall Team W L PCT W L PCT Hampton † 13 – 3 .813...

This article is part of a series aboutGeorge W. Bush Political positions Electoral history Early life Professional life Family Public image Honors 46th Governor of Texas Governorship 43rd President of the United States Presidency timeline Transition Inaugurations first second Policies Domestic Economic Foreign Bush Doctrine international trips Space Climate change Legislation and programs Pardons Appointments Cabinet Judiciary Roberts Miers Alito First term September 11 attacks War on terror...