Ötszögszámok
|
Read other articles:

Chronologies François Mitterrand lors d'un meeting électoral à Strasbourg le 19 avril.Données clés 1978 1979 1980 1981 1982 1983 1984Décennies :1950 1960 1970 1980 1990 2000 2010Siècles :XVIIIe XIXe XXe XXIe XXIIeMillénaires :-Ier Ier IIe IIIe Chronologies géographiques Afrique Afrique du Sud, Algérie, Angola, Bénin, Botswana, Burkina Faso, Burundi, Cameroun, Cap-Vert, République centrafricaine, Comores, République d...

29CuTembagaTembaga asli (berukuran ~4 cm) Garis spektrum tembagaSifat umumNama, lambangtembaga, CuPengucapan/têmbaga/[1] Penampilanmetalik merah-jinggaTembaga dalam tabel periodik 29Cu Hidrogen Helium Lithium Berilium Boron Karbon Nitrogen Oksigen Fluor Neon Natrium Magnesium Aluminium Silikon Fosfor Sulfur Clor Argon Potasium Kalsium Skandium Titanium Vanadium Chromium Mangan Besi Cobalt Nikel Tembaga Seng Gallium Germanium Arsen Selen Bromin Kripton Rubidium Strontium Yttrium ...

Untuk Golongan VIIIA, golongan paling kanan pada tabel periodik, lihat Gas mulia. Artikel utama: besi, rutenium, osmium, dan hasium Golongan 8 dalam tabel periodik Hidrogen Helium Lithium Berilium Boron Karbon Nitrogen Oksigen Fluor Neon Natrium Magnesium Aluminium Silikon Fosfor Sulfur Clor Argon Potasium Kalsium Skandium Titanium Vanadium Chromium Mangan Besi Cobalt Nikel Tembaga Seng Gallium Germanium Arsen Selen Bromin Kripton Rubidium Strontium Yttrium Zirconium Niobium Molybdenum T...

هذه المقالة عن فريق الرجال. لفريق السيدات، طالع منتخب السعودية لكرة القدم للسيدات. منتخب السعودية لكرة القدم منتخب السعودية لكرة القدم معلومات عامة اللقب الأخضر الصقور الخضر بلد الرياضة السعودية الفئة كرة القدم للرجال رمز الفيفا KSA الاتحاد الاتحاد الس�...

Ishinomaki 石巻市KotaDari atas ke bawah, kiri ke kanan : Pulau Kinkasan, Ishinomori Manga Museum, Gereja Ortodoks Santo Yohanes Rasul, Taman Hiyoriyama, dan hidangan Sasa Kamaboko. BenderaEmblemLokasi Ishinomaki di Prefektur MiyagiIshinomakiLokasi di JepangKoordinat: 38°26′03″N 141°18′10″E / 38.43417°N 141.30278°E / 38.43417; 141.30278Koordinat: 38°26′03″N 141°18′10″E / 38.43417°N 141.30278°E / 38.43417; 141.30278...

Pour les articles homonymes, voir Siège de Dantzig. Siège de Dantzig (1813) plan du siège en 1813 Informations générales Date 22 janvier 1813 au 2 janvier 1814 Lieu autour de Dantzig Issue Victoire russo-prussienne par reddition de la place Belligérants Empire français Confédération du Rhin Royaume de Bavière Royaume de Saxe Royaume de Prusse Empire russe Commandants • Jean Rapp • Matveï Platov •Alexandre de Wurtemberg • Friedrich von Löwis of Menar Forces en présence ~3...

وحدة معالجة الرسومياتمعلومات عامةصنف فرعي من coprocessor (en) معالج شعاعي جزء من بطاقة الرسوميات لديه جزء أو أجزاء texture mapping unit (en) texture cache (en) L2 cache (en) تعديل - تعديل مصدري - تعديل ويكي بيانات وحدة معالجة الرسوميات GeForce 6600GT NV43 إن وحدات معالجة الرسوميات[1] (بالإنجليزية: Graphics Processing Unit �...

Tribe of insects Diapheromerini Paraclonistria nigramal Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Arthropoda Class: Insecta Order: Phasmatodea Family: Diapheromeridae Subfamily: Diapheromerinae Tribe: Diapheromerini Diapheromerini is a tribe of walkingsticks in the family Diapheromeridae. There are at least 30 genera Diapheromerini.[1] Northern Walkingstick, Diapheromera femorata Genera These 37 genera belong to the tribe Diapheromerini: Alienobostra Zompro...

A modern trabàccolo in Cesenatico, Italy The trabàccolo, trabaccalo, trabacalo (in Italian) or trabakul (in Croatian), is a type of Adriatic Sea sailing coaster. The name comes from the word trabacca, which means tent, which in turn recalls the vessel's sails. The trabàccolo was a typical Venetian boat-form that dates back to the first half of the 15th century and that spread throughout the Adriatic. Built of oak and larch, trabàccoli were slow but reliable cargo vessels ranging between 5...

1167–1250 Italian anti-Imperial alliance For the political party, see Lega Lombarda. Member cities of the first and second Lombard League. The Lombard League (Liga Lombarda in Lombard, Lega Lombarda in Italian) was a medieval alliance formed in 1167,[1] supported by the popes, to counter the attempts by the Hohenstaufen Holy Roman emperors to assert influence over the Kingdom of Italy as a part of the Holy Roman Empire. At its apex, it included most of the cities of Northern Italy, ...

British politician from Wales, UKIP leader Neil HamiltonOfficial portrait, 2016Leader of the UK Independence PartyIncumbentAssumed office 12 September 2020[a]DeputyRebecca JanePreceded byFreddy VachhaLeader of UKIP WalesIn office26 September 2016 – 13 April 2024Leader List Diane JamesNigel Farage (acting)Paul NuttallSteve Crowther (acting)Henry BoltonGerard BattenPiers Wauchope (acting)Richard BrainePat Mountain (acting)Freddy VachhaHimself Preceded byNathan GillSucceed...

American baseball player (1860–1920) Baseball player Frank FennellyShortstopBorn: (1860-02-18)February 18, 1860Fall River, MassachusettsDied: August 14, 1920(1920-08-14) (aged 60)Fall River, MassachusettsBatted: RightThrew: RightMLB debutMay 1, 1884, for the Washington NationalsLast MLB appearanceJune 18, 1890, for the Brooklyn GladiatorsMLB statisticsBatting average.257Home runs34Runs batted in408Stolen bases175 Teams Washington Nationals (1884) Cincinnat...

Pour les articles homonymes, voir N'avoue jamais (film). N'avoue jamais Chanson de Guy Mardel auConcours Eurovision de la chanson 1965 Sortie 1965 Langue Français Genre Chanson française Auteur Françoise Dorin Compositeur Guy Mardel Chansons représentant la France au Concours Eurovision de la chanson Le Chant de Mallory(1964) Chez nous(1966)modifier N'avoue jamais est une chanson écrite par Françoise Dorin et composée et interprétée par Guy Mardel, sortie en 45 tours en 1965. C...

Sceaux 行政国 フランス地域圏 (Région) イル=ド=フランス地域圏県 (département) オー=ド=セーヌ県郡 (arrondissement) アントニー郡小郡 (canton) 小郡庁所在地INSEEコード 92071郵便番号 92330市長(任期) フィリップ・ローラン(2008年-2014年)自治体間連合 (fr) メトロポール・デュ・グラン・パリ人口動態人口 19,679人(2007年)人口密度 5466人/km2住民の呼称 Scéens地理座標 北緯48度4...

Cricket team in the Channel Islands This article is about the men's team. For the women's team, see Guernsey women's cricket team. GuernseyAssociationGuernsey Cricket BoardPersonnelCaptainMatthew StokesCoachAndrew CornfordInternational Cricket CouncilICC statusAffiliate (2005) Associate member (2008)ICC regionEuropeICC Rankings Current[1] Best-everT20I 47th 35th (2-May-2019)International cricketFirst international Guernsey v. Jersey (Saint Helier, Jersey; 14 August 1922)Twen...

Historic ranch near Santa Paula, California United States historic placeRancho CamulosU.S. National Register of Historic PlacesU.S. National Historic LandmarkCalifornia Historical Landmark No. 553 A view of Rancho Camulos from the northwest.Show map of CaliforniaShow map of the United StatesLocation5164 East Telegraph Road, Piru, CaliforniaCoordinates34°24′24″N 118°45′24″W / 34.40667°N 118.75667°W / 34.40667; -118.75667Built1853Architectural ...

Medical school affiliated with a teaching hospital An academic medical centre (AMC), variously also known as academic health science centre, academic health science system, or academic health science partnership, is an educational and healthcare institute formed by the grouping of a health professional school (such as a medical school) with an affiliated teaching hospital or hospital network. AMCs are intended to ensure that medical research breakthroughs lead to direct clinical benefits for ...

American football player and coach (born 1939) For other people named Bill Snyder, see Bill Snyder (disambiguation). Bill SnyderSnyder in 2009Current positionTitleSpecial ambassadorTeamKansas StateConferenceBig 12Biographical detailsBorn (1939-10-07) October 7, 1939 (age 84)St. Joseph, Missouri, U.S.Playing career1958Missouri1959–1962William Jewell Position(s)Quarterback, defensive backCoaching career (HC unless noted)1962Gallatin HS (MO) (assistant)1964–1965Indio HS (CA) (assistant)...

Частина серії проФілософіяLeft to right: Plato, Kant, Nietzsche, Buddha, Confucius, AverroesПлатонКантНіцшеБуддаКонфуційАверроес Філософи Епістемологи Естетики Етики Логіки Метафізики Соціально-політичні філософи Традиції Аналітична Арістотелівська Африканська Близькосхідна іранська Буддій�...
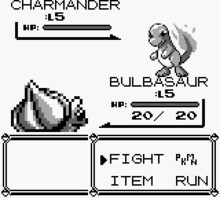
1996 video games 1996 video gamePokémon Red VersionPokémon Blue VersionPokémon Yellow VersionNorth American cover art for Pokémon Red (left), Pokémon Blue (center), and Pokémon Yellow (right)Developer(s)Game FreakPublisher(s)NintendoDirector(s)Satoshi TajiriProducer(s)Shigeru MiyamotoTakashi KawaguchiTsunekazu IshiharaDesigner(s)Satoshi TajiriProgrammer(s)Junichi MasudaShigeki MorimotoTetsuya WatanabeSousuke TamadaArtist(s)Ken SugimoriAtsuko NishidaWriter(s)Satoshi TajiriRyosuke Taniguc...





