Oszthatóság
|
Read other articles:

Rickettsia Rickettsia rickettsii (en) PenyakitPenyakit Rickettsia, rickettsialpox (en) dan rickettsiosis (en) Pewarnaan GramGram-negatif TaksonomiSuperdomainBiotaDomainBacteriaKerajaanPseudomonadatiFilumPseudomonadotaKelasAlphaproteobacteriaOrdoRickettsialesFamiliRickettsiaceaeGenusRickettsia Henrique da Rocha Lima, 1916 Tipe taksonomiRickettsia prowazekii Tata namaDinamakan berdasarkanHoward Taylor Ricketts (en) Spesies Rickettsia felis Rickettsia prowazekii Rickettsia rickettsii Rickettsia ...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Februari 2023. Alberto BarcelLahir1907ArgentinaMeninggal1975ArgentinaPekerjaanPemeranTahun aktif1948-1966 Alberto Barcel (1907–1975) adalah seorang pemeran asal Argentina. Ia tampil dalam 68 film antara 1948 dan 1966. Ia tampil dalam film Circe, yang masu...

Argentine footballer Oscar Ustari Ustari with Atlas in 2017Personal informationFull name Oscar Alfredo Ustari[1]Date of birth (1986-07-03) 3 July 1986 (age 37)[1]Place of birth América, ArgentinaHeight 1.84 m (6 ft 0 in)[1]Position(s) GoalkeeperTeam informationCurrent team Audax ItalianoYouth career Rivadavia2000–2005 IndependienteSenior career*Years Team Apps (Gls)2005–2007 Independiente 63 (1)2007–2012 Getafe 41 (0)2012–2013 Boca Juniors ...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada November 2022. Joshua K. IngallsLahir(1816-07-16)16 Juli 1816Swansea, Massachusetts, Amerika SerikatMeninggal3 Maret 1899(1899-03-03) (umur 82)Glenora, New York, Amerika SerikatPekerjaanPenemu, pendeta Kristen, penulis, reformer lahanSuami/istriAmanda Gray R...

Gambaran seniman tentang sebuah pemandangan dari eksoplanet, dengan cahaya dari awan debu antarplanet ekstrasurya Awan debu antarplanet, atau awan zodiak, terdiri dari debu kosmik (partikel kecil yang mengambang di luar angkasa) yang menyelimuti ruang antarplanet dalam sistem planet , seperti Tata Surya.[1] Sistem partikel ini telah dipelajari selama bertahun-tahun untuk memahami sifat, asal, dan hubungannya dengan benda yang lebih besar. Di Tata Surya, partikel debu antarplanet berpe...

Aron Gunnarsson Gunnarson pada tahun 2014Informasi pribadiNama lengkap Aron Einar Malmquist GunnarssonTanggal lahir 22 April 1989 (umur 34)[1]Tempat lahir Akureyri, IslandiaTinggi 5 ft 10 in (1,78 m)[1]Posisi bermain GelandangInformasi klubKlub saat ini Cardiff CityNomor 17Karier junior2004–2005 Þór AkureyriKarier senior*Tahun Tim Tampil (Gol)2005–2006 Þór Akureyri 11 (0)2006–2008 AZ 1 (0)2008–2011 Coventry City 123 (6)2011– Cardiff City 105 ...

Cristiana Carlotta di Württemberg-WinnentalMargravia di Brandeburgo-AnsbachIn carica28 agosto 1709 – 7 gennaio 1723 NascitaKirchheim unter Teck, 20 agosto 1694 MorteAnsbach, 25 dicembre 1729 Casa realeCasato del Württemberg PadreFederico Carlo di Württemberg-Winnental MadreEleonora Giuliana di Brandeburgo-Ansbach Consorte diGuglielmo Federico, margravio di Brandeburgo-Ansbach FigliCarlo Guglielmo Federico, margravio di Brandeburgo-Ansbach Cristiana Carlotta di Württemberg-Winnenta...

Wilderness park in Ontario, Canada Chiniguchi Waterway Provincial ParkIUCN category II (national park)View of Wolf LakeLocationSudbury District, Ontario, CanadaNearest citySudbury, OntarioCoordinates46°50′N 80°33′W / 46.833°N 80.550°W / 46.833; -80.550Area9,368 ha (36.17 sq mi)Established2006[1]Governing bodyOntario Parks The Chiniguchi Waterway Provincial Park consists of 9,368 ha (36.17 sq mi)[2] of prot...
Halaman ini berisi artikel tentang seluruh genus. Untuk spesies laboratorium yang paling umum digunakan, lihat Drosophila melanogaster. Untuk tipe subgenus, lihat Drosophila (upagenus). Untuk jamur yang pernah memiliki nama ini, lihat Psathyrella candolleana. Drosophila Drosophila repleta Klasifikasi ilmiah Kerajaan: Animalia Filum: Arthropoda Kelas: Insecta Ordo: Diptera Famili: Drosophilidae Tribus: Drosophilini Subtribus: Drosophilina Genus: DrosophilaFallén, 1823 Spesies tipe Musca funeb...

Voce principale: Piacenza Calcio 1919. Piacenza FCStagione 1999-2000 Sport calcio Squadra Piacenza Allenatore Luigi Simoni, poi Daniele Bernazzani e Maurizio Braghin Presidente Stefano Garilli, poi Fabrizio Garilli Serie A18º (retrocesso in Serie B) Coppa ItaliaOttavi di finale Maggiori presenzeCampionato: Roma (32)Totale: Roma (36) Miglior marcatoreCampionato: Di Napoli (4) StadioLeonardo Garilli Media spettatori10 763[1] 1998-1999 2000-2001 Si invita a seguire il modello...

Gekijōban Meiji Tokyo Renka: Hana Kagami no FantasiaNama lainJepang明治東亰恋伽~弦月の小夜曲~ SutradaraHiroshi WatanabeSkenarioYoshiko NakamuraBerdasarkanMeiji Tokyo Renkaoleh MagesPemeranSumire MorohoshiNobuhiko OkamotoDaisuke NamikawaKENNKousuke ToriumiJun FukuyamaShinnosuke TachibanaToshiyuki MorikawaYoshimasa HosoyaPenata musikImagine VoiceSinematograferAsahiko KoshiyamaPenyuntingRie MatsubaraPerusahaanproduksiStudio DeenTanggal rilis 6 Mei 2016 (2016-05-...

Nama ini menggunakan cara penamaan Portugis. Nama keluarga pertama atau maternalnya adalah Mota Veiga dan nama keluarga kedua atau paternalnya adalah de Carvalho Silva. Bernardo Silva Silva bersama Portugal pada Piala Dunia FIFA 2018Informasi pribadiNama lengkap Bernardo Mota Veiga de Carvalho e Silva[1]Tanggal lahir 10 Agustus 1994 (umur 29)Tempat lahir Lisboa, PortugalTinggi 1,73 m (5 ft 8 in)Posisi bermain Gelandang, PenyerangInformasi klubKlub saat ini Manc...

Федеральное агентство по делам Содружества Независимых Государств, соотечественников, проживающих за рубежом, и по международному гуманитарному сотрудничествусокращённо: Россотрудничество Общая информация Страна Россия Юрисдикция Россия Дата создания 6 сентября...

iOS 16 This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Applied Micro Circuits Corporation – news · newspapers · books · scholar · JSTOR (September 2007) (Learn how and when to remove this message) Applied Micro Circuits CorporationCompany typePublic:Traded asNasdaq: AMCCIndustrySemiconductors & Rela...

Spokane Neighborhood in Washington, United StatesSouthgateSpokane NeighborhoodHamblen Park in springLocation within the city of SpokaneCoordinates: 47°36′48.7″N 117°22′06.3″W / 47.613528°N 117.368417°W / 47.613528; -117.368417CountryUnited StatesStateWashingtonCountySpokaneCitySpokanePopulation (2017 [1]) • Total9,700Time zoneUTC-8 (PST) • Summer (DST)UTC-7 (PDT)ZIP Codes99203, 99223Area code509 Southgate is a neighborho...

Rock music festival in Seinäjoki, Finland This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Provinssirock – news · newspapers · books · scholar · JSTOR (March 2007) (Learn how and when to remove this message) Patti Smith at Provinssirock, 2007 HIM at Provinssirock, 2006 Provinssirock is one of the biggest roc...

Family of gastropods Pleuroceridae Io fluvialis Athearnia anthonyi Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Mollusca Class: Gastropoda Subclass: Caenogastropoda Superfamily: Cerithioidea Family: PleuroceridaeFischer, 1885 Diversity[1][2] About 150 extant species Pleuroceridae, common name pleurocerids, is a family of small to medium-sized freshwater snails, aquatic gilled gastropod mollusks in the superfamily Cerithioidea.These snails have an operc...
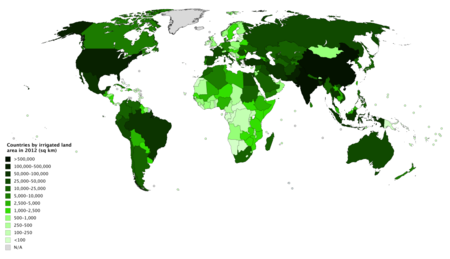
Countries by irrigated land area in 2012. Countries/territories shown with irrigated land area as '0' are shaded with the '<100' colour (lightest green); those with no data are shaded with the 'N/A' colour (grey). This is a list of countries by irrigated land area based on The World Factbook of the Central Intelligence Agency.[1] The two countries with the largest irrigated land area are India and China, which make up 22.06% and 21.33% of worldwide irrigated land area respectively...

Line of smartwatch It has been suggested that this article should be split into multiple articles. (discuss) (September 2023) Apple WatchApple Watch Series 8 in a Midnight aluminium case.DeveloperAppleManufacturerQuanta Computer[1]Compal Electronics[2](contract manufacturer)TypeSmartwatchRelease date1st generation: April 24, 2015; 9 years ago (2015-04-24)Series 1 and Series 2: September 16, 2016; 7 years ago (2016-09-16)Series 3: September&#...

This is a list of notable Malaysian politicians of Tamil origin, including original immigrants who obtained Malaysian citizenship and their Malaysian descendants. Entries on this list are demonstrably notable by having a linked current article or reliable sources as footnotes against the name to verify they are notable and define themselves either full or partial Indian origin, whose ethnic origin lie in India. This list also includes emigrant Malaysian politicians of Indian origin and could...






























































