ОеОЎОдОЋОБ ОћОЋОљ ОЏОЎОАОЋОЎ ОЕОю ОъОЕОўОЌ ОљОЋ ОДОЉОЋОдОћ ОЏОюОюОЎОф ОЎОЋОфОе ОЉОљОеОЎОЌОЎОЮ ОъОљОЋОфОЋ ОАОЋОњ.
![]() ОеОдОцОћ ОЉОЉОЎОф ОЉОЕОЏОЋОаОф ОДОўОъОЋОЪ ОЉОЎОеОЋОЕОюОЎОЮ
ОеОдОцОћ ОЉОЉОЎОф ОЉОЕОЏОЋОаОф ОДОўОъОЋОЪ ОЉОЎОеОЋОЕОюОЎОЮ
ОъОбОЉОе ОюОЕОЎОъОЋОЕ ОћОЌОЕОЋОЉ ОЕОю ОеОЎОдОЋОцОЎОЮ ОЉОЉОаОЎОЎОф ОеОдОцОћ, ОеОЎОдОЋОцОЎОЮ ОћОЮ ОаОЋОЕОљ ОЕОаОЌОДОе ОеОЉОЋОф ОЉОљОъОаОЋОф ОЋОЉОъОфОъОўОЎОДОћ. ОЏОъОЋ ОЏОЪ ОеОЎОдОЋОцОЎОЮ ОъОАОЋОњОЎОЮ ОЕОЋОаОЎОЮ ОъОЋОцОЎОбОЎОЮ ОеОЉОЋОф ОЉОўОЉОб ОћОдОЋОъОЌ ОЋОћОЌОЎ (ОЊОЋОњОъОћ ОЉОЋОюОўОф ОћОЎОљ ОЏОЋОЋОеОф ОЊОЉОЋОеОЎОЮ ОћОъОЉОЋОАОАОф ОбОю ОеОЎОдОЋОБ ОЕОю ОъОЕОЋОЕОЎОЮ), ОЋОЏОЪ ОЉОфОЋОцОбОЋОф ОцОЎОќОЎОДОюОЎОЋОф ОеОЉОЋОф.
ОеОЎОдОЋОцОЎОЮ ОЉОљОъОаОЋОф
 ОљОеОъОЋОаОЋОф ОљОюОћОъОЉОеОћ
ОљОеОъОЋОаОЋОф ОљОюОћОъОЉОеОћ
ОћОЕОЎОъОЋОЕ ОЉОдОЋОеОЋОф ОњОљОЋОъОўОеОЎОЋОф, ОЉОАОЎОъОўОеОЎОЋОф, ОЋОЉОеОЎОдОЋОцОЎОЮ ОћОЋОљ ОбОфОЎОД ОъОљОЋОЊ ОЉОљОъОаОЋОф. ОЉОћОъОЕОџ ОћОбОеОџ ОЎОЋОЉОљОЋ ОЊОЋОњОъОљОЋОф ОюОЕОЎОъОЋОЕОЎОЮ ОЉОеОЎОдОЋОцОЎОЮ ОЉОДОЎОЕОЋОўОЎОЮ ОАОЎОаОЎОЎОЮ, ОЉОдОЎОЋОеОЎ ОДОЎОе ОъОдОеОЎОЎОЮ, ОЉОДОЎОЕОЋОў ОЏОю ОЌОеОА ОЋОЉОеОЋОаОќОћ ОЉОљОЕОЋОе, ОЋОбОЋОЊ. ОъОЏОЎОЋОЋОЪ ОЕОЉОЎОћОЊОЋОф ОЋОЉОљОАОюОљОЮ ОаОљОАОе ОюОфОюОЋОф ОфОъОЋОаОЋОф ОЕОю ОЉОаОЎ ОљОЊОЮ, ОћОњОЎОбОћ ОћОљОъОаОЋОф ОЕОю ОћОЕОЎОъОЋОЕ ОЉОдОЋОеОЋОф ОњОљОЋОъОўОеОЎОЋОф ОюОъОЎОЊОф ОЕОЏОюОЋОю ОњОЊОЋОюОћ. ОљОф ОћОЕОЎОљ ОЕОю ОћОЕОЎОъОЋОЕ ОЉОеОЎОдОЋОцОЎОЮ ОаОћОЋОњ ОюОеОљОЋОф ОЉОъОАОњОЊОЎОЮ ОЋОъОЉОаОЎОЮ ОъОЋОАОюОъОЎОЮ ОъОфОДОЋОцОф ОЎОъОЎ ОћОЉОЎОаОЎОЎОЮ ОЉОљОюОћОъОЉОеОћ ОЕОЉОАОцОеОЊ.
ОЉОъОљОћ Оћ-20 ОъОљОЋОеОЎОЦ ОДОЋОеОаОюОЎОА ОљОЕОе, ОЌОДОе ОюОбОЋОъОД ОАОЋОњОЎОЮ ОЕОЋОаОЎОЮ ОЕОю ОеОЎОдОЋОцОЎОЮ ОЉОЎОдОЎОеОЋОфОЎОЋ. ОљОЕОе ОЌОДОе ОљОф ОЏОю ОћОАОЎОъОўОеОЎОЋОф ОћОЉОАОЎОАОЎОЋОф ОЕОю ОеОЎОдОЋОцОЎОЮ ОЋОЎОдОе ОеОЎОдОЋОцОЎОЮ ОЕОЉОћОЮ ОљОеОЎОЌ ОљОЌОЊ ОћОЋОцОџ ОЉОћОЊОеОњОћ ОюОљОеОЎОЌ ОљОЌОе, ОфОъОЋОаОЋОф ОЕОЉОћОЮ ОљОеОЎОЌОЎОЮ ОЎОЋОдОљОЎОЮ ОЉОћОЊОеОњОфОЎОЋОф ОъОфОЋОџ ОћОЊОБ ОЋОћОЋОцОЏОЎОЮ ОюОњОЋОцОЎОЮ ОфОюОфоЙОъОъОЊОЎОЎОЮ, ОЋОбОЋОЊ. ОљОЕОе ОЌОДОе ОњОЮ ОеОЎОдОЋОцОЎОЮ ОъОЋОЏОюОюОЎОЮ. ОЏОџ, ОюОЊОЋОњОъОћ, ОћОдОЎОЋОе "ОњОЉОЋОю ОъОбОњОю 4 - ОЕОъОЎОЮ ОЋОњОЎОћОаОЋОЮ" ОћОЋОљ ОюОъОбОЕОћ ОеОЎОдОЋОБ ОћОъОфОЉОАОА ОбОю ОъОЋОЊОю ОћОЊОЎОАОД ОЕОю ОцОЋОљОаОДОеОћ (ОљОа') (ОеОЎОдОЋОБ ОЕОю ОъОЕОўОЌ ОюОљ ОљОЋОДОюОЎОЊОЎ).
ОеОЎОдОЋОцОЎОЮ ОЉОўОЉОб
 ОЏОЋОЋОеОф ОЊОЉОЋОеОЎОЮ
ОЏОЋОЋОеОф ОЊОЉОЋОеОЎОЮ
ОаОЎОфОЪ ОюОъОдОЋОљ ОеОЎОдОЋОцОЎОЮ ОЉОъОДОЋОъОЋОф ОеОЉОЎОЮ ОЉОўОЉОб. ОЏОџ, ОюОЊОЋОњОъОћ, ОћОАОЎОЊОЋОе ОЕОю ОћОфОљОЎОЮ ОЉОЏОЋОЋОеОф ОЊОЉОЋОеОЎОЮ ОћОЋОљ ОбОю ОЉОАОЎОА ОЕОю ОеОЎОдОЋОБ ОЉОбОќОеОф ОъОЕОЋОЕОЎОЮ. ОЉОЊОЎОаОъОЎОДОћ ОюОљ ОюОЎОаОЎОљОеОЎОф ОаОЎОфОЪ ОюОъОдОЋОљ ОъОбОеОЉОЋОюОЋОф ОћОЎОЋОдОеОЋОф ОъОЉОаОЎОЮ ОЕОю ОеОЎОдОЋОцОЎОЮ. ОЏОџ, ОъОбОеОЉОЋОюОЋОф ОЕОю ОќОеОъОЎ ОюОЉОћ ОЎОЋОдОеОЋОф ОеОЎОдОЋОцОЎОЮ ОбОю ОЉОАОЎОА ОъОЕОЋОЕОЎОЮ, ОЏОъОЋ ОќОЋ ОљОЕОе ОаОЎОфОЪ ОюОъОдОЋОљ, ОюОЊОЋОњОъОћ, ОЉОЉОеОЎОЏОф ОћОъОЕОЋОЕОЎОЮ.
ОЉОњОЉОЎОЕОЎОЮ, ОћОљОўОЋОъОЎОЮ ОъОАОфОЊОеОЎОЮ ОЉОъОЉОаОћ ОъОЌОќОЋОеОЎ ОфОюОф-ОъОъОЊОЎ ОЏОџ ОЕОЌОфОџ ОЕОю ОњОЉОЎОЕ ОъОћОЋОЋОћ ОеОЎОдОЋОБ. ОљОЌОф ОъОћОЕОЎОўОЋОф ОћОъОЌОДОеОЎОЋОф ОюОЌОДОе ОъОЉОаОћ ОњОЉОЎОЕОЎ ОќОћ ОћОаОћ ОЕОЎОўОф ОћОДОеОЎОАОўОюОЋОњОеОцОЎОћ ОЉОДОеОаОЎ ОеОаОўОњОЪ. ОЉОЕОЎОўОћ ОќОЋ, ОћОњОЉОЎОЕ ОъОЋОДОеОЪ ОЉОДОеОаОЎ ОеОаОўОњОЪ ОЋОаОъОЊОЊОф ОфОЉОаОЎОф ОћОћОфОљОЉОЏОЋОф ОћОъОфОДОЉОюОф. ОћОфОъОЋОаОћ ОћОаОъОЊОЊОф ОъОћОЋОЋОћ ОюОъОбОЕОћ ОћОфОъОеОф ОцОЋОеОЎОЎОћ ОЕОю ОћОњОЉОЎОЕ, ОЋОъОДОЎОЎОъОф ОљОф ОљОЋОфОЪ ОћОАОЎОъОўОеОЎОЋОф ОЕОю ОћОЕОеОЎОњ ОћОъОЋОљОе. ОъОАОЎОЉОћ ОќОљОф ОбОЉОЋОЊОЋОф ОеОЉОЋОф, ОЏОЋОюОю ОъОдОЎОљОф 17 ОЌОЉОЋОеОЋОф ОћОАОЎОъОўОеОЎОћ ОЕОю ОеОЎОдОЋОцОЎОЮ, ОъОДОЋОеОЮ ОЉОъОЊОбОаОЎОЮ ОЕОбОАОДОЋ ОЉОДОеОЎОАОўОюОЋОњОеОцОЎОћ.
ОЎОдОЎОеОф ОеОЎОдОЋОцОЎОЮ ОъОЋОеОЏОЉОЎОЮ ОбОю ОЉОАОЎОА ОеОЎОдОЋОцОЎОЮ ОцОЕОЋОўОЎОЮ
 ОЎОдОЎОеОф ОеОЎОдОЋОцОЎОЮ ОЉОаОЋОАОЌ Оъ.ОД.ОљОЕОе
ОЎОдОЎОеОф ОеОЎОдОЋОцОЎОЮ ОЉОаОЋОАОЌ Оъ.ОД.ОљОЕОе
ОЉОфОъОЋОаОћ ОъОЋОцОЎОб ОћОАОЉОе ОЏОЎОдОЊ ОбОю ОЉОАОЎОА ОЕОю ОеОЎОдОЋОцОЎОЮ ОцОЕОЋОўОЎОЮ ОаОЎОфОЪ ОюОЉОаОЋОф ОеОЎОдОЋОцОЎОЮ ОъОАОЋОЉОЏОЎОЮ ОЎОЋОфОе, ОЏОњОЋОЪ ОљОюОЋ ОЕОљОЕОе ОћОЕОфОъОЕ ОЉОћОЮ ОЉОдОЎОЋОеОЎОЋ. ОћОћОфОЌОюОћ ОћОЎОљ ОъОљОеОЎОЌ ОцОЕОЋОў ОћОъОеОдОБ ОљОф ОћОъОЎОЕОЋОе, ОюОЊОЋОњОъОћ: ОеОЎОЉОЋОб (ОъОЕОЉОдОф 1). ОбОфОћ ОњОЋОќОеОЎОЮ ОъОћОдОюОб ОћОбОюОЎОЋОаОћ ОЕОюОЋ ОдОЋОеОћ ОЏОюОЕОћОЎ (ОъОЕОЉОдОф 2), ОЋОъОЊОЉОЎОДОЎОЮ ОљОЋОфОћ ОбОю ОћОдОюОб ОћОфОЌОфОЋОаОћ (ОъОЕОЉОдОф 3). ОъОЉОдОбОЎОЮ ОљОЋОфОћ ОцОбОЋОюОћ ОбОю ОћОдОюОбОЋОф ОћОЎОъОаОЎОф ОЋОћОЕОъОљОюОЎОф (ОъОЕОЉОдОЋОф 4,5), ОЋОюОЉОАОЋОБ ОъОфОДОЉОю ОЉОљОЋОцОЪ ОќОћ ОћОљОеОЎОЌ ОћОаОеОљОћ ОЉОъОЕОЉОдОф 6. ОЉОљОЋОфОЋ ОљОЋОцОЪ ОаОЎОфОЪ ОюОЉОаОЋОф ОеОЎОдОЋОБ ОъОЋОеОЏОЉ ОЎОЋОфОе ОЉОљОъОдОбОЋОф ОћОљОеОЎОЌ ОћОЌОЊОЕ (ОъОЕОЉОдОф 7). ОаОЎОфОЪ ОюОћОЕОЎОњ ОњОЮ ОАОЎОъОўОеОЎОћ ОЕОЋОаОћ ОбОю ОЎОЊОЎ ОАОЎОЉОЋОЉ ОЋОћОЊОЉОДОћ ОбОю ОћОдОюОб ОћОЎОъОаОЎОф.
ОеОЎОдОЋОцОЎОЮ ОЉОбОќОеОф ОъОдОЋОюОбОЎОЮ ОъОЕОЋОЏОюОюОЎОЮ
ОћОеОЎОдОЋОцОЎОЮ ОћОцОЕОЋОўОЎОЮ ОЋОћОъОЋОЏОеОЎОЮ ОЉОЎОЋОфОе ОћОЮ ОљОюОЋ ОћОаОбОЕОЎОЮ ОЉОбОќОеОф ОъОдОЋОюОбОЎОЮ ОъОЕОЋОЏОюОюОЎОЮ. ОъОЉОЎОЪ ОћОеОЎОдОЋОцОЎОЮ ОћОаОбОЕОЎОЮ ОЉОбОќОеОф ОдОЋОеОЋОф ОъОЕОЋОЏОюОюОЋОф ОЉОюОЉОЊ ОаОЎОфОЪ ОюОъОдОЋОљ ОъОАОцОе ОфОфОЎ ОДОЉОЋОдОЋОф:
ОеОЎОдОЋОцОЎОЮ ОъОЕОЋОЏОюОюОЎОЮ
ОеОЎОдОЋОцОЎОЮ ОъОЕОЋОЏОюОюОЎОЮ ОћОЮ ОеОЎОдОЋОцОЎОЮ ОћОЉОаОЋОЎОЎОЮ ОъОљОеОЎОЌ ОъОАОЋОњ ОљОЌОЊ ОћОъОћОЋОЋОћ ОъОдОЋОюОб ОъОЕОЋОЏОюОю. ОЊОеОЎОЕОћ ОаОЋОАОцОф ОћОЎОљ ОЕОћОеОЎОдОЋОБ ОЎОћОЎОћ ОдОюОб-ОюОдОюОб. ОъОЏОЎОЋОЋОЪ ОЕОАОЏОЋОЮ ОћОќОЋОЎОЋОф ОЉОЏОю ОДОЋОЊОДОЋОЊ ОЌОЎОЎОЉ ОюОћОЎОЋОф 360 ОъОбОюОЋОф, ОДОю ОюОеОљОЋОф ОЕОДОЎОЎОъОЎОЮ ОеОД 3 ОеОЎОдОЋОцОЎОЮ ОЏОљОюОЋ:
ОеОЎОдОЋОцОЎОЮ ОљОЋОаОЎОцОЋОеОъОЎОЎОЮ
ОеОЎОдОЋОцОЎОЮ ОљОЋОаОЎОцОЋОеОъОЎОЎОЮ ОћОЮ ОеОЎОдОЋОцОЎОЮ ОЉОћОЮ ОЏОю ОћОДОЋОЊОДОЋОЊОЎОЮ ОќОћОЎОЮ. ОЏОю ОћОеОЎОдОЋОцОЎОЮ ОћОъОЕОЋОЏОюОюОЎОЮ ОћОЮ ОъОАОЋОњ ОќОћ, ОЋОЉОаОЋОАОБ ОбОю ОЏОџ ОЎОЕОаОЮ ОЕОъОЋОаОћ ОАОЋОњОЎОЮ ОаОЋОАОцОЎОЮ ОЕОю ОеОЎОдОЋОцОЎОЮ ОћОъОЉОЋОАОАОЎОЮ ОбОю ОЕОЎОюОЋОЉ ОЕОю ОъОдОЋОюОбОЎОЮ ОъОЕОЋОЏОюОюОЎОЮ ОЎОЌОЊ. ОеОЎОдОЋОцОЎОЮ ОљОюОЋ ОаОДОеОљОЎОЮ ОњОЮ ОеОЎОдОЋОцОЎОЮ ОАОъОЎ-ОъОЕОЋОЏОюОюОЎОЮ ОљОЋ ОеОЎОдОЋОцОЎОЮ ОљОеОЏОЎОъОЊОЎОЎОЮ.
-
Snub Hexagonal Tiling
-
Trihexagonal Tiling
-
Elongated Triangular Tiling
-
Snub Square Tiling
-
Small Rhombitrihexagonal Tiling
-
Truncated Square Tiling
-
Truncated Hexagonal Tiling
-
Great Rhombitrihexagonal Tiling
ОАОЎОъОўОеОЎОЋОф ОЕОю ОеОЎОдОЋОцОЎОЮ
ОЏОю ОћОеОЎОдОЋОцОЎОЮ ОЕОћОЋОдОњОЋ ОбОЊ ОЏОћ ОћОЮ ОеОЎОдОЋОцОЎОЮ ОъОЌОќОЋОеОЎОЎОЮ, ОЏОюОЋОъОе, ОеОЎОдОЋОцОЎОЮ ОЕОАОЎОъОўОеОЎОЎОЮ ОфОЌОф ОцОбОЋОюОф ОћОќОќОћ, ОЉОЕОаОЎ ОЏОЎОЋОЋОаОЎОЮ ОЕОЋОаОЎОЮ. ОЉОаОЋОАОБ ОюОАОЎОъОўОеОЎОћ ОюОћОќОќОЋОф, ОюОеОЎОдОЋОБ ОбОЕОЋОЎОЋОф ОюОћОЎОЋОф ОАОЎОъОўОеОЎОЋОф ОаОЋОАОцОЋОф. ОюОЊОЋОњОъОћ, ОћОеОЎОдОЋОБ ОъОеОЎОЉОЋОбОЎОЮ (ОюОЋОЌ ОъОЕОЉОдОЋОф) ОАОЎОъОўОеОЎ ОњОЮ ОюОАОЎОЉОЋОЉОЎОЮ ОЉ-90 ОъОбОюОЋОф ОЋОЏОъОЋ ОЏОЪ ОюОЕОЎОДОЋОцОЎОЮ ОЉОљОеОЉОбОћ ОЏОЎОЋОЋОаОЎОЮ ОЕОЋОаОЎОЮ: ОЕОЎОДОЋОБ ОљОаОЏОЎ ОЊОеОџ ОъОеОЏОќ ОћОеОЎОЉОЋОб, ОЕОЎОДОЋОБ ОљОЋОцОДОЎ ОЋОЏОЪ ОЕОЎОДОЋОцОЎОЮ ОЊОеОџ ОЕОаОЎ ОћОљОюОЏОАОЋОаОЎОЮ ОЕОю ОћОеОЎОЉОЋОб.
ОаОЎОфОЪ ОюОАОЋОЋОњ ОеОЎОдОЋОцОЎОЮ ОюОцОЎ ОћОАОЎОъОўОеОЎОЋОф ОЕОћОЮ ОъОДОЎОЎОъОЎОЮ, ОћОљОеОЋОќОЋОф ОЉОЌОЉОЋОеОф ОћОАОЎОъОўОеОЎОЋОф. ОюОцОбОЋОюОЋОф ОћОЎОЋОдОеОЋОф ОАОЎОъОўОеОЎОЋОф ОДОЋОеОљОЎОЮ ОљОЎОќОЋОъОўОеОЎОЋОф. ОцОбОЋОюОЋОф ОљОюОЋ ОаОЎОфОаОЋОф ОюОћОњОЊОеОћ ОбОю ОЎОЊОЎ ОцОЋОаОДОдОЎОћ ОћОцОЋОбОюОф ОбОю ОЏОю ОћОаОДОЋОЊОЋОф ОЉОъОЎОЕОЋОе ОфОЋОџ ОЕОъОЎОеОф ОъОеОЌОД ОЏОџ ОЕОћОъОеОЌОД ОЉОЎОЪ ОЕОфОЎ ОаОДОЋОЊОЋОф ОЎОћОЎОћ ОЕОЋОЋОћ ОюОъОеОЌОД ОЕОю ОћОфОъОЋОаОЋОф ОЕОю ОЕОфОЎ ОћОаОДОЋОЊОЋОф. ОЎОЕОаОЮ ОљОеОЉОбОћ ОАОЋОњОЎОЮ ОЕОю ОљОЎОќОЋОъОўОеОЎОЋОф: ОћОќОќОЋОф, ОАОЎОЉОЋОЉОЎОЮ, ОЕОЎОДОЋОцОЎОЮ ОЋОЏОЪ ОЕОЎОДОЋОБ ОњОюОЎОЕОћ - ОцОбОЋОюОћ ОћОъОЕОюОЉОф ОЕОЎОДОЋОБ ОЋОњОюОЎОЕОћ. ОаОЎОфОЪ ОюОћОЋОЏОЎОЌ ОЏОЎ ОеОЎОдОЋОцОЎОЮ ОъОЌОќОЋОеОЎОЎОЮ ОЎОЏОЋОюОЎОЮ ОюОћОЎОЋОф ОАОЎОъОўОеОЎОЎОЮ ОюОАОЎОЉОЋОЉ ОеОД ОЉОАОЎОЉОЋОЉОЎОЮ ОЕОћОЮ ОЏОцОЋОюОЋОф ОЕОю 90 ОъОбОюОЋОф ОљОЋ ОЕОю 60 ОъОбОюОЋОф.
ОДОЉОЋОдОф ОЏОю ОћОАОЎОъОўОеОЎОЋОф ОЕОю ОеОЎОдОЋОБ ОъОћОЋОЋОћ ОЌОЉОЋОеОћ. ОаОЎОфОЪ ОюОћОЋОЏОЎОЌ ОЕОЎОЕОаОЪ ОеОД 17 ОЌОЉОЋОеОЋОф ОЕОеОЎОдОЋОБ ОъОЌОќОЋОеОЎ ОЎОЏОЋОю ОюОДОЎОЎОЮ (ОћОаОДОеОљОЋОф wallpaper group). ОЉОфОъОЋОаОЋОф ОюОћОюОЪ ОаОЎОфОЪ ОюОеОљОЋОф ОЊОЋОњОъОљОЋОф ОюОЏОю ОљОЌОф Оъ-17 ОЌОЉОЋОеОЋОф ОћОАОЎОъОўОеОЎОћ, ОЋОЏОЪ ОљОф ОћОЕОЮ ОћОДОеОЎОАОўОюОЋОњОеОцОЎ ОЕОюОћОЪ. ОеОљОЋ ОњОЮ ОЌОЉОЋОеОф ОАОЎОъОўОеОЎОЋОф ОаОДОЋОЊОфОЎОф.
-
ОћОЌОЉОЋОеОћ p1: ОљОЎОЪ ОАОЎОъОўОеОЎОЋОф ОљОЌОеОЋОф ОюОъОбОў ОћОќОќОЋОф
-
ОћОЌОЉОЋОеОћ p2: ОъОЏОЎОюОћ ОАОЎОъОўОеОЎОЋОф ОюОћОќОќОћ ОЋОЏОЪ ОюОАОЎОЉОЋОЉ ОЉ-180 ОъОбОюОЋОф. (ОћОфОъОЋОаОћ ОюОДОЋОЌОћ ОъОЕОўОЎОЌ
ОъОдОеОЎ)
-
ОћОЌОЉОЋОеОћ pm: ОбОЉОЋОеОћ ОДОЎОЎОъОф ОњОЮ ОАОЎОъОўОеОЎОћ ОюОЕОЎОДОЋОБ ОЉОдОЎОе ОљОЌОЊ
-
ОћОЌОЉОЋОеОћ pg: ОбОЉОЋОеОћ ОДОЎОЎОъОЎОЮ ОњОюОЎОЕОћ-ОЕОЎОДОЋОБ ОљОџ ОюОљ ОДОЎОЎОъОф ОАОЎОъОўОеОЎОћ ОюОАОЎОЉОЋОЉОЎОЮ ОљОЋ ОЕОЎОДОЋОцОЎОЮ.
-
ОћОЌОЉОЋОеОћ pmm: ОДОЎОЎОъОЎОЮ ОЕОЎОДОЋОцОЎОЮ ОЉОЕОаОЎ ОдОЎОеОЎОЮ ОаОЎОдОЉОЎОЮ ОЋОЏОЪ 4 ОъОеОЏОќОЎОЮ ОюОАОЎОЉОЋОЉОЎОЮ ОЉ-180 ОъОбОюОЋОф (ОћОдОЎОюОЋОЮ ОћОЋОљ ОЕОю
ОњОЊОе ОбОЦ ОЉ
ОљОеОдОЋОф ОћОЉОеОЎОф)
-
ОћОЌОЉОЋОеОћ pmg: ОДОЎОЎОъОЎОЮ ОЕОаОЎ ОдОЎОеОЎОЮ ОЕОю ОАОЎОЉОЋОЉ ОЉ-180 ОъОбОюОЋОф, ОдОЎОе ОЕОЎОДОЋОБ ОљОЌОЊ ОЋОдОЎОе ОљОЌОЊ ОЕОю ОњОюОЎОЕОћ-ОЕОЎОДОЋОБ (ОћОдОЎОюОЋОЮ ОћОЋОљ ОЕОю
ОеОДОъОћ Оъ
ОћОЋОЋОљОЎ)
-
ОћОЌОЉОЋОеОћ pgg: ОЕОаОЎ ОдОЎОеОЎОЮ ОюОАОЎОЉОЋОЉ ОЉ- 180 ОъОбОюОЋОф ОЋОЏОЪ ОЕОаОЎ ОдОЎОеОЎОЮ ОљОаОЏОЎОЎОЮ ОЕОю ОњОюОЎОЕОћ-ОЕОЎОДОЋОБ (ОћОдОЎОюОЋОЮ ОћОЋОљ ОЕОю ОъОЊОеОЏОћ ОЉ
ОЉОЋОЊОцОЕОў)
-
ОћОЌОЉОЋОеОћ cmm: ОъОЏОЎОюОћ ОЕОЎОДОЋОцОЎОЮ ОЉОЕОаОЎ ОдОЎОеОЎОЮ ОЕОЋОаОЎОЮ ОЋОЏОЪ ОАОЎОЉОЋОЉОЎОЮ ОЉ- 180 ОъОбОюОЋОф (ОћОдОЎОюОЋОЮ ОћОЋОљ ОЕОю ОДОЎОе ОюОЉОаОЎОЮ)
-
ОћОЌОЉОЋОеОћ p4: ОЉОЌОЉОЋОеОћ ОќОљОф ОЕОаОЎ ОъОеОЏОќОЎОЮ ОюОАОЎОЉОЋОЉОЎОЮ ОЉ-90 ОъОбОюОЋОф ОЋОъОеОЏОќ ОљОЌОЊ ОюОАОЎОЉОЋОЉОЎОЮ ОЉ-180 ОъОбОюОЋОф. (ОћОдОЎОюОЋОЮ ОћОЋОљ ОЕОю ОфОДОеОф ОДОЉОе ОъОдОеОЎ)
-
ОћОЌОЉОЋОеОћ p4m: ОДОЎОЎОъОЎОЮ ОЕОаОЎ ОъОеОЏОќОЎОЮ ОюОАОЎОЉОЋОЉОЎОЮ ОЉОЏОцОЋОюОЋОф ОЕОю 90 ОъОбОюОЋОф ОЋОЏОЪ ОљОеОЉОбОћ ОдОЎОеОЎОЮ ОюОЕОЎОДОЋОцОЎОЮ
-
ОћОЌОЉОЋОеОћ p4g: ОДОЎОЎОъОЎОЮ ОЕОаОЎ ОъОеОЏОќОЎОЮ ОюОАОЎОЉОЋОЉОЎОЮ ОЉОЏОцОЋОюОЋОф ОЕОю 90 ОъОбОюОЋОф ОљОџ ОеОД ОЕОаОЎ ОдОЎОеОЎОЮ ОюОЕОЎОДОЋОцОЎОЮ ОЋОЏОЪ ОЕОаОЎ ОдОЎОеОЎОЮ ОюОЕОЎОДОЋОБ-ОњОюОЎОЕОћ (ОћОдОЎОюОЋОЮ ОћОЋОљ ОЕОю
ОцОЋОеОдОюОЪ ОАОЎОаОЎ)
-
ОћОЌОЉОЋОеОћ p3: ОъОЏОЎОюОћ ОЕОюОЋОЕОћ ОъОеОЏОќОЎОЮ ОюОАОЎОЉОЋОЉОЎОЮ ОЉОЏОцОЋОюОЋОф ОЕОю 120, ОљОЉОю ОюОљ ОъОЏОЎОюОћ ОЕОЎОДОЋОцОЎОЮ ОљОЋ ОЕОЎОДОЋОБ ОњОюОЎОЕОћ (ОћОдОЎОюОЋОЮ ОћОЋОљ ОЕОю ОдОЎОЋОе ОДОЎОе Оъ
ОљОюОћОъОЉОеОћ ОЉ
ОАОцОеОЊ)
-
ОћОЌОЉОЋОеОћ p3m1: ОъОЏОЎОюОћ 3 ОдОЎОеОЎОЮ ОюОЕОЎОДОЋОцОЎОЮ, 3 ОъОеОЏОќОЎОЮ ОюОАОЎОЉОЋОЉОЎОЮ ОЉОЏОцОЋОюОЋОф ОЕОю 120 ОъОбОюОЋОф ОЕОЏОю ОљОЌОЊ ОъОћОЮ ОаОъОдОљ ОбОю ОдОЎОе ОЕОЎОДОЋОБ ОЋ-3 ОдОЎОеОЎОЮ ОЕОю ОЕОЎОДОЋОБ-ОњОюОЎОЕОћ
-
ОћОЌОЉОЋОеОћ p31m: ОЏОъОЋ ОћОЌОЉОЋОеОћ ОћОДОЋОЊОъОф ОћОЎОљ ОъОЏОЎОюОћ ОЕОюОЋОЕОћ ОъОеОЏОќОЎОЮ ОюОАОЎОЉОЋОЉОЎОЮ ОъОАОЊОе ОЕОюОЎОЕОЎ (ОЏОцОЋОюОЋОф ОЕОю 120 ОъОбОюОЋОф), ОЋОЕОюОЋОЕОћ ОдОЎОеОЎОЮ ОЕОю ОЕОЎОДОЋОцОЎОЮ ОљОЉОю ОћОъОеОЏОќ ОЕОю ОюОцОЌОЋОф ОљОЌОЊ ОћОАОЎОЉОЋОЉОЎОЮ ОюОљ ОаОъОдОљ ОбОю ОдОЎОе ОЕОЎОДОЋОБ. ОЏОъОЋ ОЏОЪ ОЎОЕОаОЮ ОЕОюОЋОЕОћ ОдОЎОеОЎОЮ ОЕОю ОЕОЎОДОЋОБ-ОњОюОЎОЕОћ (ОћОдОЎОюОЋОЮ ОћОЋОљ ОЕОю ОцОЋОеОдОюОЪ ОАОЎОаОЎ)
-
ОћОЌОЉОЋОеОћ p6: ОъОЏОЎОюОћ ОАОЎОЉОЋОЉОЎОЮ ОЉОЏОцОЋОюОЋОф ОЕОю 60 ОъОбОюОЋОф ОЉОюОЉОЊ (ОЉОфОъОЋОаОћ ОДОЎОЕОЋОў
ОцОеОАОЎ)
-
ОћОЌОЉОЋОеОћ p6m: ОъОЏОЎОюОћ ОАОЎОЉОЋОЉОЎОЮ ОЉОЏОцОЋОюОЋОф ОЕОю 60 ОЋОЏОЪ ОЕОЎОДОЋОцОЎОЮ ОЉ-6 ОдОЎОеОЎОЮ (ОЉОфОъОЋОаОћ ОеОЎОдОЋОБ ОцОеОАОЎ)
ОеОЎОдОЋОБ ОЉОљОъОдОбОЋОф ОъОдОЋОюОбОЎОЮ ОДОъОЋОеОЎОЮ
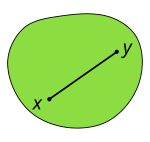 ОдОЋОеОћ ОДОъОЋОеОћ - ОћОЎОЕОе ОћОъОЌОЉОе ОЏОю ОЕОфОЎ ОаОДОЋОЊОЋОф ОћОЕОЎОЎОЏОЋОф ОюОдОЋОеОћ ОбОЋОЉОе ОЉОфОЋОЏОћ ОдОЋОеОћ ОДОъОЋОеОћ - ОћОЎОЕОе ОћОъОЌОЉОе ОЏОю ОЕОфОЎ ОаОДОЋОЊОЋОф ОћОЕОЎОЎОЏОЋОф ОюОдОЋОеОћ ОбОЋОЉОе ОЉОфОЋОЏОћ
|
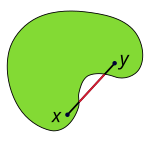 ОдОЋОеОћ ОЕОљОЎОаОаОћ ОДОъОЋОеОћ ОдОЋОеОћ ОЕОљОЎОаОаОћ ОДОъОЋОеОћ
|
ОъОдОЋОюОб ОДОъОЋОе ОћОЋОљ ОъОдОЋОюОб ОЕОбОЉОЋОеОЋ ОћОДОЋ ОћОъОЌОЉОе ОЉОЎОЪ ОЏОю ОЕОфОЎ ОаОДОЋОЊОЋОф ОбОЋОЉОе ОЉОфОЋОџ ОћОъОдОЋОюОб. ОЏОю ОъОЕОЋОюОЕ ОЋОЏОЪ ОЏОю ОъОеОЋОЉОб ОДОъОЋОеОЎОЮ ОЎОЏОЋОюОЎОЮ ОюОеОдОБ ОљОф ОћОъОЎОЕОЋОе. ОюОбОЋОъОф ОќОљОф, ОъОдОЋОюОб ОДОъОЋОе ОЉОбОю ОЕОЉОб ОдОюОбОЋОф ОљОЋ ОЎОЋОфОе ОюОљ ОЎОЏОЋОю ОюОеОдОБ ОљОф ОћОъОЎОЕОЋОе. ОбОЉОЋОе ОъОЌОЋОъОЕОЎОЮ ОЋОъОЕОЋОЕОЎОЮ ОћОЉОбОЎОћ ОДОдОф ОЎОЋОфОе ОъОАОЋОЉОЏОф, ОЕОЏОЪ, ОюОЊОЋОњОъОћ, ОЉОбОќОеОф ОћОъОЌОЋОъОЕ ОћОъОЕОЋОЏОюОю ОюОљ ОаОЎОфОЪ ОюОеОдОБ ОљОф ОћОъОЎОЕОЋОе, ОљОџ ОбОЮ ОќОљОф ОЎОЕОаОЮ ОъОЌОЋОъОЕОЎОЮ ОљОЌОеОЎОЮ ОЕОљОЎОфОЮ ОЏОЪ ОаОЎОфОЪ ОюОеОдОБ ОљОф ОћОъОЎОЕОЋОе. ОаОЋОЕОљ ОћОЌОЎОцОЋОЕ ОљОЌОе ОАОЋОњОЎОЮ ОЕОю ОъОдОЋОюОбОЎОЮ ОДОъОЋОеОЎОЮ ОљОЎОфОЮ ОаОЎОфОЪ ОюОеОдОБ ОљОф ОћОъОЎОЕОЋОе ОћОбОАОЎОД ОъОфОъОўОЎОДОљОЎОЮ ОеОЉОЎОЮ.
ОЉОЕОаОф 1968 ОаОеОљОћ ОћОЎОћ ОЕОћОЉОбОЎОћ ОаОцОфОеОћ, ОъОЏОЎОЋОЋОЪ ОЕОћОъОфОъОўОЎОДОљОЎ ОеОЎОд'ОеОЊ ОДОеОЕОаОе ОўОбОЪ ОЉОбОЉОЋОЊОф ОћОЊОЋОДОўОЋОеОў ОЕОюОЋ ОЕОћОдОюОЎОЌ ОюОАОЋОЋОњ ОљОф ОЏОю ОАОЋОњОЎ ОћОъОЌОЋОъОЕОЎОЮ ОЋОћОъОЕОЋОЕОЎОЮ ОЉОбОќОеОфОЮ ОаОЎОфОЪ ОюОеОдОБ ОљОф ОћОъОЎОЕОЋОе. ОбОЊ ОюОЕОаОф 1968 ОћОЎОЋ ОЎОЊОЋОбОЎОЮ ОеОД 5 ОАОЋОњОЎОЮ ОЕОЋОаОЎОЮ ОЕОю ОъОЌОЋОъОЕОЎОЮ ОЏОљОюОЋ ОЋОДОеОЕОаОе ОћОдОюОЎОЌ ОюОъОдОЋОљ 3 ОАОЋОњОЎОЮ ОаОЋОАОцОЎОЮ ОЋОЏОЪ "ОюОћОЋОЏОЎОЌ" ОЕОљОюОЋ ОЏОю ОАОЋОњОЎ ОћОъОЌОЋОъОЕОЎОЮ ОћОљОцОЕОеОЎОЎОЮ. ОЉОЕОаОф 1975 ОцОеОАОЮ ОъОеОўОЎОЪ ОњОеОЊОаОе ОЉОўОЋОе ОћОЎОЊОЋОб ОЕОюОЋ ОЉОАОЎОЎОаОўОЎОцОЎОД ОљОъОеОЎОДОЪ ОъОљОъОе ОбОю ОЉОбОЎОћ ОќОЋ, ОЎОЌОЊ ОбОЮ ОћОфОЋОдОљОЋОф ОЕОю ОДОеОЕОаОе. ОљОЌОЊ ОъОДОЋОеОљОЎОЋ ОЕОю ОњОеОЊОаОе, ОъОфОЏОаОф ОъОЌОЕОЉОЎОЮ ОЉОЕОЮ ОеОЎОд'ОеОЊ Оњ'ОЎОЎОъОА ОћОЕОюОЎОЕОЎ, ОћОЌОюОЎОў ОюОЌОцОЕ ОљОЌОе ОцОфОеОЋОЪ ОюОЌОЎОЊОћ ОъОЉОюОЎ ОюОДОеОЋОљ ОљОф ОћОцОфОеОЋОаОЋОф ОЕОю ОДОеОЕОаОе. ОћОЋОљ ОљОЏОЪ ОћОдОюОЎОЌ ОюОъОдОЋОљ ОъОЌОЋОъОЕ ОћОъОеОдОБ ОљОф ОћОъОЎОЕОЋОе ОЋОюОћОцОфОбОфОЋ ОћОъОЌОЋОъОЕ ОюОљ ОаОЏОюОю ОЉ-8 ОћОАОЋОњОЎОЮ ОЕОфОЋОљОеОЋ ОбОю ОЎОЊОЎ ОДОеОЕОаОе. ОъОЏОљОЪ, ОЕОЉОћОЋОЏОЌОћ ОЕОю ОДОеОЕОаОе ОаОцОюОћ ОўОбОЋОф ОЋОћОЉОбОЎОћ ОаОцОфОЌОћ ОъОЌОЊОЕ. ОћОаОЋОЕОљ ОћОдОЎОф ОљОф ОЊОъОЎОЋОаОћ ОЕОю ОъОеОњ'ОЋОеОЎ ОеОЎОЎОА (Marjorie Rice), ОбОДОеОф ОЉОЎОф ОъОцОюОЋОеОЎОЊОћ, ОЕОъОдОљОћ ОЉОеОЎОдОЋОцОЎОЮ ОЕОЎОюОЋОЉ ОЉОЎОЪ ОљОћОЉОфОћ ОюОъОфОъОўОЎОДОћ ОЋОљОћОЉОфОћ ОюОљОъОаОЋОф. ОеОЎОЎОА ОћОЌОюОћ ОюОЌОДОЋОе ОЉОдОЋОеОћ ОЕОЎОўОфОЎОф ОљОф ОАОЋОњОЎ ОћОеОЎОдОЋОцОЎОЮ ОЕОцОЋОеОАОъОЋ ОЋОюОЌОцОЕ ОљОЌОе ОЌОЊОЕОЎОЮ, ОЋОюОдОЋОеОџ ОЏОџ ОцОЎОфОЌОћ ОюОбОдОъОћ ОъОбОЎОЪ ОљОюОњОЉОеОћ ОъОЎОЋОЌОЊОф ОъОЕОюОћ. ОћОъОљОъОдОЎОЮ ОЕОюОћ ОаОЕОљОЋ ОцОеОЎ ОЋОбОЊ ОюОЕОаОф 1977 ОћОЎОљ ОћОдОюОЎОЌОћ ОюОъОдОЋОљ 3 ОАОЋОњОЎОЮ ОаОЋОАОцОЎОЮ ОЕОю ОъОЌОЋОъОЕОЎОЮ ОљОЎОфОЮ ОаОЎОфОЪ ОюОеОдОБ ОљОф ОћОъОЎОЕОЋОе ОЋОЏОЪ 60 ОАОЋОњОЎОЮ ОЕОю ОеОЎОдОЋОцОЎОЮ ОЉОбОќОеОф ОъОЌОЋОъОЕОЎОЮ ОЕОюОљ ОћОЎОЋ ОЎОЊОЋОбОЎОЮ ОДОЋОЊОЮ ОюОЏОЪ. ОЉОЕОаОф 1985, ОАОўОЋОЊОаОў ОњОеОъОаОЎ ОЉОЕОЮ ОеОЋОюОБ ОЕОўОЎОЎОЪ ОъОдОљ ОАОЋОњ ОаОЋОАОБ ОЕОю ОъОЌОЋОъОЕ ОћОъОеОдОБ ОљОф ОћОъОЎОЕОЋОе, ОЉОЕОаОф 2015 ОъОдОљОЋ ОЕОюОЋОЕОћ ОъОфОъОўОЎОДОљОЎОЮ (Mann/McLoud/Von Derau) ОъОљОЋОаОЎОЉОеОАОЎОўОф ОЋОЋОЕОЎОаОњОўОЋОЪ ОЉОЉОЋОф'ОљОю ОАОЋОњ ОаОЋОАОБ ОЕОю ОъОЌОЋОъОЕ. ОЉОАОџ ОћОЏОю ОЎОЊОЋОбОЎОЮ 15 ОАОЋОњОЎОЮ ОЕОю ОъОЌОЋОъОЕОЎОЮ ОДОъОЋОеОЎОЮ ОЕОЉОљОцОЕОеОЋОфОЮ ОюОеОдОБ ОљОф ОћОъОЎОЕОЋОе.
ОеОЎОдОЋОцОЎОЮ ОюОљ ОъОЌОќОЋОеОЎОЎОЮ
ОЉОбОЎОЋОф ОћОЌОюОўОћ ОЋОљОеОЎОЌОЎ ОЋОљОаОњ
ОћОЕОљОюОћ ОћОљОЮ ОЎОЕ ОДОЉОЋОдОћ ОЕОю ОљОеОЎОЌОЎОЮ ОЉОбОќОеОфОЮ ОаОЎОфОЪ ОюОеОдОБ ОљОф ОћОъОЎОЕОЋОе, ОљОџ ОюОљ ОаОЎОфОЪ ОюОеОдОцОЋ ОЉОдОЋОеОћ ОъОЌОќОЋОеОЎОф ОћОфОбОЋОеОеОћ ОюОеОљОЕОЋОаОћ ОЉОћОъОЕОџ ОюОЉОбОЎОћ Оћ-18 Оъ-23 ОћОЉОбОЎОЋОф ОЕОю ОћОЎОюОЉОеОў, ОЋОцОбОЮ ОаОЋОАОцОф ОЉОЕОаОф 1961 ОЏОљОЕОе ОћОюОЋОњОЎОДОљОЎ ОћОљОЋ ОЋОљОаОњ (Hao Wang) ОбОАОД ОЉОЉОбОЎОЎОф ОћОЊОЋОъОЎОаОЋ. ОЉОбОЎОЎОф ОћОЊОЋОъОЎОаОЋ ОћОЎОљ ОЉОбОЎОЎОф ОћОЏОеОбОћ, ОћОЊОЋОеОЕОф ОюОќОћОЋОф ОћОљОЮ ОАОў ОаОфОЋОЪ ОЕОю ОљОеОЎОЌОЎОЮ ОЎОЏОЋОю ОюОеОдОБ ОљОф ОћОъОЎОЕОЋОе ОљОЋ ОюОљ. ОЋОљОаОњ ОћОеОљОћ ОЏОЎ ОЎОЕОаОЋ ОљОюОњОЋОеОЎОфОЮ ОћОцОЋОфОе ОЉОбОЎОћ ОќОЋ, ОЉОфОаОљОЎ ОЕОЏОю ОАОў ОАОЋОцОЎ ОЕОю ОљОеОЎОЌОЎОЮ ОћОъОеОдОБ ОљОф ОћОъОЎОЕОЋОе ОЎОЏОЋОю ОюОеОдОБ ОљОЋОфОЋ ОЉОдОЋОеОћ ОъОЌОќОЋОеОЎОф. ОћОЌОю ОъОЕОаОф 1966 ОћОЌОюОЋ ОюОћОфОњОюОЋОф ОАОўОЎОЮ ОЕОю ОљОеОЎОЌОЎОЮ ОЕОъОћОЋОЋОЎОЮ ОЊОЋОњОъОљОЋОф ОаОњОЊОЎОЋОф: ОћОЮ ОъОАОЋОњОюОЎОЮ ОюОеОдОБ ОљОф ОћОъОЎОЕОЋОе ОеОД ОЉОдОЋОеОћ ОюОљ ОъОЌОќОЋОеОЎОф, ОЋОљОюОЋ ОаОДОеОљОЎОЮ ОбОю ОЕОъОЋ ОљОеОЎОЌОЎ ОЋОљОаОњ. ОДОеОЋОЉОћ ОюОќОћ ОЉОбОЎОЎОф ОћОњОеОбОЎОЪ, ОћОЕОЋОљОюОф ОљОЮ ОљОцОЕОе ОюОеОдОБ ОљОф ОћОъОЎОЕОЋОе ОЉОАОў ОаОфОЋОЪ ОЕОю ОљОеОЎОЌОЎОЮ, ОЏОЕОъОфОЌОЎОюОЎОЮ ОъОфОдОЋОеОћ ОъОАОЋОЎОъОф ОЕОю ОћОљОеОЎОЌОЎОЮ.
 ОљОеОЎОЌОЎ ОеОЋОЉОЎОаОАОЋОЪ
ОљОеОЎОЌОЎ ОеОЋОЉОЎОаОАОЋОЪ
ОЉОЕОаОф 1966 ОћОдОюОЎОЌ ОеОЋОЉОеОў ОЉОеОњОе (Robert Berger) ОюОъОдОЋОљ ОАОў ОЕОъОЏОЎОю 20,426 ОљОеОЎОЌОЎ ОЋОљОаОњ. ОЉОћОъОЕОџ ОћОдОюОЎОЌ ОЉОеОњОе ОюОдОъОдОЮ ОљОф ОъОАОцОе ОћОљОеОЎОЌОЎОЮ Ою-104, ОЋОћОаОА ОюОЋо╣ОЎОЏОюОЎ (Hans L├цuchli) ОћОдОюОЎОЌ ОюОћОЋОеОЎОЊ ОљОф ОћОъОАОцОе Ою-40. ОЉОЕОаОф 1971 ОћОдОюОЎОЌ ОеОцОљОю ОеОЋОЉОЎОаОАОЋОЪ (Raphael M. Robinson) ОюОЎОдОЋОе ОАОў ОљОеОЎОЌОЎ ОЋОљОаОњ ОћОъОЏОЎОю ОеОД 6 ОљОеОЎОЌОЎОЮ. ОцОеОў ОюОћОцОеОЏОф ОћОЕОбОеОфОЋ ОЕОю ОЋОљОаОњ, ОЉОеОњОе ОЋОеОЋОЉОЎОаОАОЋОЪ ОњОЮ ОћОдОЎОњОЋ ОћОЋОЏОЌОћ ОюОЏОџ ОЕОюОљ ОДОЎОЎОЮ ОљОюОњОЋОеОЎОфОЮ ОъОћОАОЋОњ ОћОъОЉОЋОДОЕ - ОЏОюОЋОъОе, ОЉОбОЎОЎОф ОћОЊОЋОъОЎОаОЋ ОћОЎОљ ОЉОбОЎОћ ОюОљ ОЏОеОЎОбОћ. ОћОћОЋОЏОЌОћ ОъОфОЉОАОАОф ОбОю ОЉОЎОдОЋОб ОАОЎОъОЋОюОдОЎОћ ОЕОю ОеОЎОдОф ОъОЏОЋОаОф ОўОЎОЋОеОЎОаОњ ОЉОљОъОдОбОЋОф ОљОеОЎОЌОЎ ОЋОљОаОњ ОЋОћОфОЉОАОАОЋОф ОбОю ОљОЎ ОЏОеОЎОбОЋОф ОЉОбОЎОЎОф ОћОбОдОЎОеОћ. ОЉОЏОџ ОъОЋОЊОњОЮ ОЕОЉОбОЎОЋОф ОеОЎОдОЋОБ "ОъОАОфОЎОеОЋОф" ОЉОфОЋОЏОЪ ОъОЋОЊОю ОЌОЎОЕОЋОЉОЎ ОюОљ ОўОеОЎОЋОЋОЎОљОюОЎ. ОЉОЕОаОф 1973 ОЌОюОћ ОћОфОДОЊОъОЋОф ОњОЊОЋОюОћ ОЏОљОЕОе ОћОцОЎОќОЎОДОљОЎ ОеОЋОњ'Ое ОцОаОеОЋОќ ОъОдОљ 3 ОАОўОЎОЮ ОаОЋОАОцОЎОЮ ОЕОю ОљОеОЎОЌОЎОЮ ОЏОљОюОЋ, ОЏОџ ОЕОЉОЏОю ОАОў ОЎОЕОаОЮ ОЕОаОЎ ОљОеОЎОЌОЎОЮ ОЉОюОЉОЊ. ОЉОЕОаОф 1977 ОцОеОАОЮ ОеОЋОЉОеОў ОљОъОЪ (Robert Ammann) ОЏОъОћ ОАОўОЎОЮ ОаОЋОАОцОЎОЮ.
ОЏОљОъОЋОе, ОеОЎОдОЋОцОЎ ОцОаОеОЋОќ (Penrose tiling) ОћОфОњОюОЋ ОбОю ОЎОЊОЎ ОеОЋОњ'Ое ОцОаОеОЋОќ ОЉОЕОаОф 1973, ОЋОюОъОбОЕОћ ОћОЋОљ ОњОЎОюОћ ОъОАОцОе ОќОЋОњОЋОф ОЕОю ОљОеОЎОЌОЎОЮ ОЏОљОюОЋ ОЉОбОќОеОфОЮ ОаОЎОфОЪ ОюОеОдОБ ОљОф ОћОъОЎОЕОЋОе ОљОџ ОюОљ ОЉОдОЋОеОћ ОъОЌОќОЋОеОЎОф. ОЉОфОъОЋОаОЋОф ОюОъОўОћ ОаОЎОфОЪ ОюОъОдОЋОљ ОљОф ОЕОаОЎ ОћОќОЋОњОЋОф ОћОъОцОЋОеОАОъОЎОЮ ОЉОЎОЋОфОе, ОќОЋОњ ОћОъОбОЋОЎОаОЎОЮ ОЋОћОќОЋОњ ОћОДОеОЋОЎ "ОћОбОцОЎОцОЋОЪ ОЋОћОЌОЦ". ОцОаОеОЋОќ ОАОЎОцОе ОЕОћОћОЕОеОљОћ ОюОеОЎОдОЋОцОЎОЮ ОћОљОюОЋ ОЉОљОћ ОъОфОЋОџ ОДОеОЎОљОф ОћОАОцОе Harmonis Mondis ОЕОю ОЎОЋОћОљОаОА ОДОцОюОе, ОЕОбОАОД ОЉОЎОЪ ОћОЎОфОе ОњОЮ ОЉОеОЎОдОЋОцОЎОЮ.
-
ОљОеОЎОЌОЎ ОцОаОеОЋОќ ОћОъОЉОЋОАОАОЎОЮ ОбОю ОъОбОЋОЎОаОЎОЮ
-
ОеОЎОдОЋОБ ОЕОаОЉОаОћ ОЉОљОъОдОбОЋОф ОљОеОЎОЌОЎ ОцОаОеОЋОќ ОћОъОбОЋОЎОаОЎОЮ
-
ОеОЎОдОЋОБ 'ОЏОЋОЏОЉ' ОЉОљОъОдОбОЋОф ОљОеОЎОЌОЎ ОцОаОеОЋОќ
-
ОћОбОцОЎОцОЋОЪ ОЋОћОЌОЦ.
ОеОЎОдОЋОБ ОћОЏОЋОЏОЉ ОъОеОљОћ ОЏОъОћ ОъОћОфОЏОЋОаОЋОф ОћОъОеОфОДОЋОф ОЕОю ОеОЎОдОЋОцОЎ ОцОаОеОЋОќ. ОеОљОЕОЎОф ОаОЎОфОЪ ОюОеОљОЋОф ОЕОюОеОЎОдОЋОБ ОЎОЕ ОфОЏОЋОаОћ ОЕОю ОЊОъОЎОЋОЪ ОбОдОъОЎ - ОаОЎОфОЪ ОюОЉОаОЋОф ОЉОбОќОеОфОЋ ОбОЋОфОДОЎОЮ ОњОЊОЋОюОЎОЮ ОЎОЋОфОе ОЋОЎОЋОфОе ОЕОю ОћОЏОЋОЏОЉ. ОЉОаОЋОАОБ ОюОеОЎОдОЋОБ ОЎОЕ ОАОЎОъОўОеОЎОћ ОюОАОЎОЉОЋОЉОЎОЮ ОъОАОЊОе ОЌОъОЎОЕОЎ, ОАОЎОЉОЋОЉОЎОЮ ОЉ 360/5=72 ОъОбОюОЋОф.
ОеОЎОдОЋОцОЎ ОцОаОеОЋОќ ОќОЏОЋ ОюОцОеОАОЋОЮ ОњОЊОЋОю ОЉОбОДОЉОЋОф ОЏОфОЉОћ ОЕОцОеОАОЮ ОбОюОЎОћОЮ ОъОеОўОЎОЪ ОњОеОЊОаОе ОЉОўОЋОеОЋ, ОљОџ ОќОЏОЋ ОюОфОћОЋОЊОћ ОњОЊОЋОюОћ ОЉОћОеОЉОћ ОЉОќОЏОЋОф ОћОњОЎОюОЋОЎ ОЕОю ОњОЉОЎОЕОЎОЮ ОЏОъОЋ-ОъОЌОќОЋОеОЎОЎОЮ (Quasicrystals) ОЉОЕОаОф 1982. ОЉОЕОаОф 1982 ОњОЎОюОћ ОцОеОЋОц' ОЊОЪ ОЕОЏОўОъОЪ ОъОћОўОЏОаОЎОЋОЪ ОЉОЎОЕОеОљОю ОњОЉОЎОЕ ОЉОбОю ОАОЎОъОўОеОЎОћ ОљОЎОДОЋОАОћОЊОеОюОЎОф, ОЏОюОЋОъОе ОЉОбОю ОАОЎОъОўОеОЎОћ ОюОАОЎОЉОЋОЉОЎОЮ ОЉ-72 ОъОбОюОЋОф. ОЕОЏОўОъОЪ ОъОЊОЊ ОфОъОЋОаОЋОф ОеОаОўОњОЪ ОЕОю ОњОЉОЎОЕОЎОЮ ОћОъОдОЎОњОЋОф ОАОЎОъОўОеОЎОћ ОќОЋ ОЉОдОЋОеОћ ОЉОеОЋОеОћ. ОЉОфОЌОЎОюОћ, ОаОфОДОюОћ ОћОфОњОюОЎОф ОЉОЌОЋОАОе ОљОъОЋОЪ ОЕОю ОћОДОћОЎОюОћ ОћОъОЊОбОЎОф, ОЏОЎОЋОЋОЪ ОЕОћОљОъОЋОаОћ ОћОеОЋОЋОЌОф ОћОЎОЎОфОћ ОЏОЎ ОњОЉОЎОЕОЎОЮ ОъОЌОќОЋОеОЎОЎОЮ ОљОЎОаОЮ ОЎОЏОЋОюОЎОЮ ОюОћОЎОЋОф ОЉОбОюОЎ ОАОЎОъОўОеОЎОћ ОъОАОЋОњ ОќОћ. ОћОфОњОюОЎОф ОћОфОцОеОАОъОћ ОеОД ОЕОаОфОЎОЎОЮ ОъОљОЋОЌОе ОЎОЋОфОе, ОЉ-1984. ОЏОЌОЋОЊОЕ ОюОљОЌОе ОћОцОеОАОЋОЮ, ОћОЋОдОбОћ ОфОљОЋОеОЎОћ ОюОцОЎОћ ОљОцОЕОе ОюОћОАОЉОЎОе ОљОф ОћОфОЋОдОљОЋОф ОЕОю ОЕОЏОўОъОЪ ОЉОбОќОеОф ОеОЎОдОЋОцОЎ ОцОаОеОЋОќ. ОфОњОюОЎОф ОќОљОф ОЌОЋОюОюОћ ОАОбОеОћ ОњОЊОЋОюОћ ОЋОъОћОцОЏОћ ОъОЌОЕОЉОфОЎОф ОЉОфОЌОЋОЮ ОћОъОдОЉ ОћОъОбОЋОЉОћ. ОљОЌОеОЎОћ ОћОфОњОюОЋ ОњОЉОЎОЕОЎОЮ ОЏОъОЋ-ОъОЌОќОЋОеОЎОЎОЮ ОеОЉОЎОЮ ОаОЋОАОцОЎОЮ. ОбОю ОфОњОюОЎОф ОќОЋ ОќОЏОћ ОЕОЏОўОъОЪ ОЉОцОеОА ОаОЋОЉОю ОюОЏОЎОъОЎОћ ОюОЕОаОф 2011.
ОеОЎОдОЋОБ ОАОцОЎОеОюОЎ
ОАОцОЎОеОюОћ ОЎОЏОЋОюОћ ОюОеОдОБ ОљОф ОћОъОЎОЕОЋОе, ОбОЮ ОЌОюОДОЎОЮ ОљОЕОе ОќОћОЎОЮ ОќОћ ОюОќОћ ОљОЋ ОбОЮ ОЌОюОДОЎОЮ ОћОЋОюОЏОЎОЮ
ОЋОњОЊОюОЎОЮ[1].
ОћОъОДОеОћ ОћОеОљОЕОЋОЪ ОъОЋОЊОњОЮ ОЉОљОъОдОбОЋОф ОеОЎОдОЋОБ ОЋОЋОЊОеОЉОеОњ, ОЕОњОЎОюОћ ОћОљОаОА ОЋОЋОЊОеОЉОеОњ (Voderberg) ОЉОЕОаОф 1936, ОЋОаОЎОфОЪ ОњОЮ ОюОъОдОЋОљ ОЊОЋОњОъОљОЋОф ОЕОюОЋ ОЉОўОЉОб, ОЉОљОЉОДОаОЎ ОцОеОЌОЎОЮ ОюОъОЕОю.
ОћОъОДОеОћ ОћОЕОаОЎ ОЕОю ОеОЎОдОЋОБ ОАОцОЎОеОюОЎ ОћОЋОљ ОЌОюОДОЎОЮ ОЊОЋОъОЎОЮ ОќОћ ОюОќОћ ОљОџ ОћОЋОюОЏОЎОЮ ОЋОњОЊОюОЎОЮ, ОеОЎОдОЋОБ ОъОАОЋОњ ОќОћ ОаОДОеОљ ОеОЎОдОЋОБ ОАОцОЎОеОюОЎ ОюОЋОњОеОЎОфОъОЎ. ОЊОЋОњОъОљОЋОф ОюОеОЎОдОЋОБ ОюОЋОњОеОЎОфОъОЎ ОаОЎОфОЪ ОюОъОдОЋОљ ОЉОўОЉОб, ОЉОДОЋОаОЏОЎОЎОф ОћОаОљОЋОўОЎОюОЋОА, ОЏОъОЋ ОњОЮ ОЉОеОЎОдОЋОцОЎОЮ ОъОбОЕОћ ОљОЊОЮ.[2] ОћОњОЋОЊОю ОЕОю ОЏОю ОљОеОЎОЌ ОњОЊОЋОю ОъОДОЋОЊОъОЋ ОцОЎ ОъОАОцОе ОДОЉОЋОб, ОЏОџ ОЕОћОњОЊОюОЎОЮ ОаОфОЋОаОЎОЮ ОбОю ОАОЋОюОЮ ОюОЋОњОеОЎОфОъОЎ ОЋОъОЏОљОЪ ОћОЕОЮ. ОаОЎОфОЪ ОюОћОЌОЕОЎОЉ ОеОЎОдОЋОБ ОАОцОЎОеОюОЎ ОюОЋОњОеОЎОфОъОЎ ОњОЮ ОЏОАОЋОњ ОЕОю ОеОЎОдОЋОБ ОЉОбОю ОЊОъОЎОЋОЪ ОбОдОъОЎ.
-
ОДОЋОаОЏОЎОЎОф ОаОљОЋОўОЎОюОЋОА ОЌОдОЋОЎОћ ОюОЕОаОЎОЎОЮ, ОћОъОъОЌОЎОЕОћ ОеОЎОдОЋОБ ОЉОљОъОдОбОЋОф ОАОцОЎОеОюОћ ОюОЋОњОеОЎОфОъОЎОф
-
ОеОЎОдОЋОБ ОЋОЋОЊОеОЉОеОњ, ОеОЎОдОЋОБ ОАОцОЎОеОюОЎ ОЉОљОъОдОбОЋОф ОЌОюОДОЎОЮ ОќОћОЎОЮ
-
ОљОЉОДОаОЎ ОцОеОЌ ОћОъОЊОњОЎОъОЎОЮ ОеОЎОдОЋОБ ОАОцОЎОеОюОЎ ОЉОљОъОдОбОЋОф ОЌОюОДОЎОЮ ОќОћОЎОЮ (ОъОеОЋОЉОбОЎОЮ)
-
ОъОЊОеОњОЋОф ОАОцОЎОеОюОЎОЋОф ОЉ
ОъОЋОќОЎОљОЋОЪ ОћОЋОЋОфОЎОДОЪ
ОЊОъОЎОЋОЪ ОбОдОъОЎ, ОцОеОДОўОюОЎОЮ ОЋОеОЎОдОЋОцОЎОЮ
ОъОеОўОЎОЪ ОњОеОЊОаОе ОаОфОЪ ОљОф ОћОЕОЮ ОеОцОўОЎОю (Reptile) ОюОдОЋОеОЋОф ОЕОаОЎОфОЪ ОюОЉОаОЋОф ОбОЋОфОД ОъОЋОњОЊОю ОЕОюОћОЪ ОЉОбОќОеОф ОъОАОцОе ОбОЋОфОДОЎОЮ ОДОўОаОЎОЮ. ОЊОЋОњОъОћ ОцОЕОЋОўОћ ОюОЏОџ ОћОЎОљ ОћОеОЎОЉОЋОб; ОЉОбОќОеОф 4 ОеОЎОЉОЋОбОЎОЮ ОДОўОаОЎОЮ ОќОћОЎОЮ ОаОЎОфОЪ ОюОЉОаОЋОф ОеОЎОЉОЋОб ОњОЊОЋОю ОЎОЋОфОе. ОЏОю ОдОЋОеОћ ОъОћОАОЋОњ ОћОќОћ ОЎОЏОЋОюОћ ОюОЕОъОЕ ОњОЮ ОюОеОЎОдОЋОБ ОЕОю ОћОъОЎОЕОЋОе ОЏОЋОюОЋ, ОбОю ОЎОЊОЎ ОЌОќОеОћ ОбОю ОћОцОбОЋОюОћ ОъОАОцОе ОњОЊОЋОю ОЕОю ОцОбОъОЎОЮ. ОЉОљОЎОЋОе ОаОЎОфОЪ ОюОеОљОЋОф ОЏОЎОдОЊ ОЉОљОъОдОбОЋОф ОдОЋОеОћ ОћОаОДОеОљОф L ОўОеОЋОъОЎОаОЋ ОаОЎОфОЪ ОюОЉОаОЋОф ОеОЎОдОЋОБ ОЕОю ОћОъОЎОЕОЋОе ОЉОЕОюОЉОЎОЮ.
ОЏОъОЋ ОЉОЊОЋОњОъОћ ОЕОю Оћ- L ОўОеОЋОъОЎОаОЋ ОаОЎОфОЪ ОюОеОљОЋОф ОЕОеОЎОдОЋОцОЎОЮ ОћОаОЉОаОЎОЮ ОЉОЕОЎОўОћ ОќОљОф ОљОЎОаОЮ ОЉОћОЏОеОЌ ОъОЌОќОЋОеОЎОЎОЮ. ОЉОЕОЎОўОћ ОќОљОф ОаОЎОфОЪ ОюОЉОаОЋОф ОеОЎОдОЋОцОЎОЮ ОЕОю ОћОъОЎОЕОЋОе ОњОЮ ОъОцОеОДОўОюОЎОЮ. ОюОЊОЋОњОъОћ, ОъОЕОЋОюОЕ ОЕОеОцОЎОаОАОДОЎ ОћОЋОљ ОеОцОўОЎОю ОЋОюОЏОЪ ОаОЎОфОЪ ОюОеОдОБ ОљОф ОћОъОЎОЕОЋОе ОЏОЋОюОЋ ОЉОбОќОеОф ОъОЕОЋОюОЕОЎ ОЕОеОцОЎОаОАОДОЎ.
ОћОЏОюОюОЋОф
ОљОЋОъОеОЎОЮ ОЕОДОЉОЋОдОћ ОЌОАОЋОъОћ ОЋОъОЊОЎОЊОћ X ОъОеОдОцОф ОЉОћОќОќОЋОф ОљОф ОћОъОеОЌОЉ ОћОљОЋОДОюОЎОЊОЎ, ОљОЮ ОДОЎОЎОъОф ОДОЉОЋОдОћ (ОЊОЎОАОДОеОўОЎОф) L ОЏОџ ОЕОЏОъОбОў ОЏОю ОаОДОЋОЊОћ ОъОЋОцОЎОбОћ ОЉОЊОЎОЋОД ОЉОљОЌОф ОћОћОќОќОЋОф  (ОбОЉОЋОе
(ОбОЉОЋОе  ). ОюОфОЏОЋОаОћ ОќОЋ ОЎОЕ ОДОЕОе ОЌОќОД ОюОДОЎОЋОъОЋ ОЕОю ОЉОАОЎОА ОљОЋОеОфОЋОаОЋОеОъОюОЎ ОЕОю ОцОЋОаОДОдОЎОЋОф ОљОДОАОцОЋОаОаОдОЎОљОюОЎОЋОф ОюОъОеОЌОЉ ОћОцОЋОаОДОдОЎОЋОф
). ОюОфОЏОЋОаОћ ОќОЋ ОЎОЕ ОДОЕОе ОЌОќОД ОюОДОЎОЋОъОЋ ОЕОю ОЉОАОЎОА ОљОЋОеОфОЋОаОЋОеОъОюОЎ ОЕОю ОцОЋОаОДОдОЎОЋОф ОљОДОАОцОЋОаОаОдОЎОљОюОЎОЋОф ОюОъОеОЌОЉ ОћОцОЋОаОДОдОЎОЋОф  , ОЕОћОЋОЉОЎОю ОюОћОЕОбОеОф ОцОЋОњОюОЎОЊ (ОљОа'), ОюОцОЎОћ ОДОЉОЋОдОћ X ОъОеОдОцОф ОљОф ОћОъОеОЌОЉ ОћОљОЋОДОюОЎОЊОЎ (ОЉОћОќОќОЋОф) ОљОЮ ОЋОеОД ОљОЮ ОЎОЕ ОюОъОеОЌОЉ ОћОцОЋОаОДОдОЎОЋОф ОЕОюОћ ОЉОАОЎОА ОЏОа"Ою. ОћОЕОбОеОћ ОќОЋ ОћОЋОцОеОЏОћ ОЉ-2004 ОбОю ОЎОЊОЎ ОўОеОаОА ОўОљОЋ ОЉОъОъОЊ 5 ОЋОъОбОюОћ (ОЋОљОЌОе-ОЏОџ ОњОЮ ОЉОъОъОЊОЎОЮ 3 ОЋ-4). ОЏОю ОњОЋОБ ОДОъОЋОе ОћОъОеОдОБ ОљОф ОћОъОеОЌОЉ ОћОљОЋОДОюОЎОЊОЎ ОћОЋОљ ОцОљОЋОЪ. ОљОЋОъОеОЎОЮ ОЕОцОљОЋОЪ ОћОЋОљ ОАОЎОъОўОеОЎ ОюОЕОЎОДОЋОБ ОљОЮ ОћОЋОљ ОАОЎОъОўОеОЎ ОЉОЎОЌОА ОюОЕОЎОДОЋОБ ОАОЉОЎОЉ ОъОеОЏОќ ОћОЏОЋОЉОЊ ОЕОюОЋ. ОцОљОЋОЪ ОДОъОЋОе ОъОеОдОБ ОљОф ОћОъОеОЌОЉ (ОЉОћОќОќОЋОф) ОљОЮ ОЋОеОД ОљОЮ (1) ОћОЋОљ ОАОЎОъОўОеОЎ ОюОЕОЎОДОЋОБ, (2) ОЏОю ОЊОЋОцОЪ ОЕОюОЋ (ОЏОюОЋОъОе ОцОљОћ ОъОДОЋ-ОъОъОЊ 1) ОАОЎОъОўОеОЎОф ОюОЕОЎОДОЋОБ, ОЋ-(3) ОЉОЏОю ОъОЌОюОДОф ОћОќОќОћ ОЕОю ОцОљОћ ОъОДОЋ-ОъОъОЊ 2 ОЎОЕ ОЉОЊОЎОЋОД 4 ОљОЋ 6 ОцОљОЋОф (McMullen, 1980). ОЉОцОеОў, ОћОцОљОЋОаОЎОЮ ОћОДОъОЋОеОЎОЮ ОћОъОеОдОцОЎОЮ (ОЉОћОќОќОЋОф) ОљОф ОћОъОЎОЕОЋОе ОћОЮ (ОбОЊ ОЏОЊОЎ ОћОбОфОДОћ ОљОцОЎОаОЎОф) ОћОъОДОЉОЎОюОЎОф ОЋОћОъОЕОЋОЕОћ ОћОАОЎОъОўОеОЎ ОЉОюОЉОЊ; ОЎОЕ 5 ОцОљОЋОаОЎОЮ ОДОъОЋОеОЎОЮ ОћОъОеОдОцОЎОЮ (ОЉОћОќОќОЋОф) ОљОф ОћОъОеОЌОЉ ОћОфОюОф-ОъОъОЊОЎ; ОЋ-52 ОћОъОеОдОцОЎОЮ (ОЉОћОќОќОЋОф) ОљОф ОћОъОеОЌОЉ Оћ-4 ОъОъОЊОЎ.
, ОЕОћОЋОЉОЎОю ОюОћОЕОбОеОф ОцОЋОњОюОЎОЊ (ОљОа'), ОюОцОЎОћ ОДОЉОЋОдОћ X ОъОеОдОцОф ОљОф ОћОъОеОЌОЉ ОћОљОЋОДОюОЎОЊОЎ (ОЉОћОќОќОЋОф) ОљОЮ ОЋОеОД ОљОЮ ОЎОЕ ОюОъОеОЌОЉ ОћОцОЋОаОДОдОЎОЋОф ОЕОюОћ ОЉОАОЎОА ОЏОа"Ою. ОћОЕОбОеОћ ОќОЋ ОћОЋОцОеОЏОћ ОЉ-2004 ОбОю ОЎОЊОЎ ОўОеОаОА ОўОљОЋ ОЉОъОъОЊ 5 ОЋОъОбОюОћ (ОЋОљОЌОе-ОЏОџ ОњОЮ ОЉОъОъОЊОЎОЮ 3 ОЋ-4). ОЏОю ОњОЋОБ ОДОъОЋОе ОћОъОеОдОБ ОљОф ОћОъОеОЌОЉ ОћОљОЋОДОюОЎОЊОЎ ОћОЋОљ ОцОљОЋОЪ. ОљОЋОъОеОЎОЮ ОЕОцОљОЋОЪ ОћОЋОљ ОАОЎОъОўОеОЎ ОюОЕОЎОДОЋОБ ОљОЮ ОћОЋОљ ОАОЎОъОўОеОЎ ОЉОЎОЌОА ОюОЕОЎОДОЋОБ ОАОЉОЎОЉ ОъОеОЏОќ ОћОЏОЋОЉОЊ ОЕОюОЋ. ОцОљОЋОЪ ОДОъОЋОе ОъОеОдОБ ОљОф ОћОъОеОЌОЉ (ОЉОћОќОќОЋОф) ОљОЮ ОЋОеОД ОљОЮ (1) ОћОЋОљ ОАОЎОъОўОеОЎ ОюОЕОЎОДОЋОБ, (2) ОЏОю ОЊОЋОцОЪ ОЕОюОЋ (ОЏОюОЋОъОе ОцОљОћ ОъОДОЋ-ОъОъОЊ 1) ОАОЎОъОўОеОЎОф ОюОЕОЎОДОЋОБ, ОЋ-(3) ОЉОЏОю ОъОЌОюОДОф ОћОќОќОћ ОЕОю ОцОљОћ ОъОДОЋ-ОъОъОЊ 2 ОЎОЕ ОЉОЊОЎОЋОД 4 ОљОЋ 6 ОцОљОЋОф (McMullen, 1980). ОЉОцОеОў, ОћОцОљОЋОаОЎОЮ ОћОДОъОЋОеОЎОЮ ОћОъОеОдОцОЎОЮ (ОЉОћОќОќОЋОф) ОљОф ОћОъОЎОЕОЋОе ОћОЮ (ОбОЊ ОЏОЊОЎ ОћОбОфОДОћ ОљОцОЎОаОЎОф) ОћОъОДОЉОЎОюОЎОф ОЋОћОъОЕОЋОЕОћ ОћОАОЎОъОўОеОЎ ОЉОюОЉОЊ; ОЎОЕ 5 ОцОљОЋОаОЎОЮ ОДОъОЋОеОЎОЮ ОћОъОеОдОцОЎОЮ (ОЉОћОќОќОЋОф) ОљОф ОћОъОеОЌОЉ ОћОфОюОф-ОъОъОЊОЎ; ОЋ-52 ОћОъОеОдОцОЎОЮ (ОЉОћОќОќОЋОф) ОљОф ОћОъОеОЌОЉ Оћ-4 ОъОъОЊОЎ.
ОюОеОЎОдОЋОцОЎОЮ ОЎОЕ ОЌОЕОЎОЉОЋОф ОеОЉОћ ОЉОњОљОЋОъОўОеОЎОћ (ОЋОЉОўОЋОцОЋОюОЋОњОЎОћ ОљОюОњОЉОеОЎОф), ОЉОЏОџ ОЕОћОЮ ОъОљОцОЕОеОЎОЮ ОюОюОъОЋОЊ ОљОф ОћОДОЉОЋОдОћ ОћОъОЏОЋОАОћ X ОбОю ОЎОЊОЎ ОфОЏОЋОаОЋОф ОЕОю ОћОЏОЎОАОЋОЎ. ОюОЏОЎОАОЋОЎ ОъОЕОЋОЎОЏОф ОЌОЉОЋОеОћ G. ОЉОъОДОеОћ ОЕОћОЌОЉОЋОеОћ ОцОЋОбОюОф ОЉОљОЋОцОЪ ОўОеОаОќОЎОўОЎОЉОЎ, ОћОљОеОЎОЌОЎОЮ ОЉОћОЏОеОЌ ОЌОЋОцОцОЎОЮ ОќОћ ОюОќОћ, ОЋОљОцОЕОе ОюОћОфОљОЎОЮ ОЉОЎОаОЎОћОЮ ОюОЉОЎОЪ ОъОеОЌОЉ ОћОъОаОћ  . ОДОЕОеОЎОЮ ОљОюОћ ОћОЮ ОаОДОЋОЊОф ОћОъОЋОдОљ ОЕОю ОфОЋОЏОаОЎОфОЋ ОЕОю ОцОюОЎОДОА ОДОюОЎОЎОЪ ОъОАОЋОБ ОћОъОљОћ Оћ-19, ОюОюОъОЋОЊ ОъОеОЌОЉОЎОЮ ОњОљОЋОъОўОеОЎОЎОЮ ОЊОеОџ ОћОЌОЉОЋОеОЋОф ОћОцОЋОбОюОЋОф ОбОюОЎОћОЮ, ОЋОюОћОцОџ.
. ОДОЕОеОЎОЮ ОљОюОћ ОћОЮ ОаОДОЋОЊОф ОћОъОЋОдОљ ОЕОю ОфОЋОЏОаОЎОфОЋ ОЕОю ОцОюОЎОДОА ОДОюОЎОЎОЪ ОъОАОЋОБ ОћОъОљОћ Оћ-19, ОюОюОъОЋОЊ ОъОеОЌОЉОЎОЮ ОњОљОЋОъОўОеОЎОЎОЮ ОЊОеОџ ОћОЌОЉОЋОеОЋОф ОћОцОЋОбОюОЋОф ОбОюОЎОћОЮ, ОЋОюОћОцОџ.
ОЕОбОЕОЋОбОЎ ОъОфОъОўОЎОДОћ ОћОДОЕОЋОеОЎОЮ ОЉОеОЎОдОЋОцОЎОЮ
ОцОЋОюОЎОљОЋОъОЎОаОЋ
 ОбОеОџ ОъОЋОеОЌОЉ РђЊ ОцОЋОюОЎОљОЋОъОЎОаОЋ
ОбОеОџ ОъОЋОеОЌОЉ РђЊ ОцОЋОюОЎОљОЋОъОЎОаОЋ
 ОљОеОЉОб ОъОЕОцОЌОЋОф ОћОцОЋОюОЎОљОЋОъОЎОаОЋОЎОЮ ОћОеОљОЕОЋОаОЋОф
ОљОеОЉОб ОъОЕОцОЌОЋОф ОћОцОЋОюОЎОљОЋОъОЎОаОЋОЎОЮ ОћОеОљОЕОЋОаОЋОф
ОЉОЕОаОф 1953 ОћОдОЎОњ ОАОЋОюОЋОъОЋОЪ ОњОЋОюОЋОъОЉ (Solomon W. Golomb) ОљОф ОћОъОЋОаОЌ ОцОЋОюОЎОљОЋОъОЎОаОЋ (polyomino), ОћОъОфОљОе "ОЎОдОЋОеОЎОЮ" (ОЕОюОбОЎОфОЎОЮ ОъОЏОЋОаОЎОЮ "Lattice Animals") ОћОъОЋОеОЏОЉОЎОЮ ОъОЌОЎОЉОЋОе ОЕОю ОъОАОцОе ОеОЎОЉОЋОбОЎОЮ ОќОћ ОюОќОћ (ОюОљОЋОеОџ ОЕОцОфОЎОћОЮ). ОћОцОЋОюОЎОљОЋОъОЎОаОЋ ОъОЌОЋОюОДОЎОЮ ОюОъОЕОцОЌОЋОф ОюОцОЎ ОъОАОцОе ОћОеОЎОЉОЋОбОЎОЮ ОЕОћОЎОдОЋОеОЎОЮ ОъОЏОЎОюОЎОЮ: ОћОъОЋОаОЋОъОЎОаОЋ ОъОЏОЎОю ОеОЎОЉОЋОб ОљОЌОЊ, ОћОЊОЋОъОЎОаОЋ ОЉОаОЋОЎ ОъОЕОаОЎ ОеОЎОЉОЋОбОЎОЮ, ОћОўОеОЋОъОЎОаОЋ ОъОЕОюОЋОЕОћ (ОЋОЎОЕОаОЮ ОЕОаОЎ ОЎОдОЋОеОЎОЮ ОЉОъОЕОцОЌОф ОћОўОеОЋОъОЎОаОЋОЎОЮ) ОћОўОўОеОЋОъОЎОаОЋ ОЉОаОЋОЎОЎОЮ ОъОљОеОЉОбОћ ОеОЎОЉОЋОбОЎОЮ (ОЋОЎОЕОаОЮ 5 ОЎОдОЋОеОЎОЮ ОЕОЋОаОЎОЮ ОЏОљОюОЋ, ОћОъОЏОЏОЉОЎОЮ, ОЎОЌОЊ ОбОЮ ОЕОЎОДОЋОцОЎОЮ ОЕОюОћОЮ, ОЉОъОЕОЌОД ОћОўОўОеОЎОА) ОЋОЏОџ ОћОюОљОћ. ОЉОбОДОЉОЋОф ОћОъОдОљОф ОћОцОЋОюОЎОљОЋОъОЎОаОЋ ОћОЌОю ОюОћОЎОЋОЋОдОе ОњОю ОњОЊОЋОю ОЕОю ОЌОЎОЊОЋОф ОћОДОЕОЋОеОЋОф ОљОюОЎОћОЪ ОЋОеОЋОЉОЮ ОДОЕОЋОеОЋОф ОюОеОЎОдОЋОцОЎОЮ ОЉОбОќОеОф ОћОцОЋОюОЎОљОЋОъОЎОаОЋ. ОћОЌОЎОЊОћ ОћОъОцОЋОеОАОъОф ОЉОЎОЋОфОе ОЉОћОДОЕОе ОќОћ ОћОЎОљ ОћОљОЮ ОаОЎОфОЪ ОюОеОдОБ ОюОЋОЌ ОЕОЌОъОў 8x8 ОЕОъОъОаОЋ ОћОЋОеОЎОЊОЋ ОљОф ОЕОфОЎ ОћОцОЎОаОЋОф ОћОаОњОЊОЎОЋОф, ОЉОбОќОеОф ОЌОфОЎОЏОЋОф ОЕОю ОЊОЋОъОЎОаОЋ ОЉОюОЉОЊ. ОЕОљОюОћ ОЕОАОЉОЎОЉОћ ОЎОЕ ОЕОбОЕОЋОбОЎОЮ ОљОюОЋ ОдОЋОеОЋОф ОъОфОЋОџ ОћОцОЋОюОЎОљОЋОъОЎОаОЋ ОъОАОЋОњОюОЎОЮ ОюОеОдОБ ОљОф ОћОъОЎОЕОЋОе ОЏОЋОюОЋ? ОЌОЎОЊОЋОф ОаОЋОАОцОЋОф ОаОЋОњОбОЋОф ОюОеОЎОдОЋОцОЎОЮ ОЕОю ОдОЋОеОЋОф ОАОцОдОЎОцОЎОЋОф ОюОЊОЋОњОъОћ ОЏОЎОдОЊ ОаОЎОфОЪ ОюОеОдОБ ОъОюОЉОЪ ОЉОњОЋОЊОю 6x10 ОЉОбОќОеОф 12 ОдОЋОеОЋОф ОћОцОаОўОЋОъОЎОаОЋ?
ОћОЉОбОЎОЋОф Оћ"ОЏОюОюОЎОЋОф" ОЉОЎОЋОфОе ОћОДОЕОЋОеОЋОф ОЉОцОЋОюОЎОљОЋОъОЎОаОЋ ОЏОЉОе ОќОЏОЋ ОюОфОЋОдОљОЋОф ОЕОюОЎОюОЎОЋОф; ОЕОљОюОф ОеОЎОдОЋОБ ОћОъОЎОЕОЋОе ОЉОЎОЊОЎ ОДОЉОЋОдОћ ОЕОеОЎОеОЋОфОЎОф ОЕОю ОцОЋОюОЎОљОЋОъОЎОаОЋОЎОЮ ОћОЎОљ ОЉОюОфОЎ ОЏОеОЎОбОћ, ОЉОЊОЋОъОћ ОюОЉОбОЎОЎОф ОеОЎОдОЋОБ ОћОъОЎОЕОЋОе ОбОю ОЎОЊОЎ ОљОеОЎОЌОЎ ОЋОљОаОњ (ОћОеОљОЕОЋОЪ ОЕОћОеОљОћ ОќОљОф ОћОЎОћ ОњОЋОюОЋОъОЉ ОбОдОъОЋ, ОЕОЉОЎОдОб ОеОЊОЋОДОдОЎОћ ОъОЉОбОЎОЎОф ОћОеОЎОдОЋОБ ОЕОю ОЋОљОаОњ), ОЋОљОЎОюОЋ ОћОЉОбОЎОћ ОЕОю ОеОЎОдОЋОБ ОЕОўОЌ ОаОфОЋОЪ ОЋОАОЋОцОЎ ОЏОюОЕОћОЋ ОЉОбОќОеОф ОДОЉОЋОдОћ ОЕОеОЎОеОЋОфОЎОф ОЕОю ОцОЋОюОЎОљОЋОъОЎОаОЋ ОћОЎОљ ОЉОбОЎОћ NP-ОЕОюОъОћ, ОЋОюОЏОЪ ОюОљ ОАОЉОЎОе ОЕОЎОЎОъОдОљ ОюОћ ОцОфОеОЋОЪ ОЎОбОЎОю ОЌОЎОЕОЋОЉОЎОф.
ОћОЏОюОюОЋОф ОЕОю ОцОЋОюОЎОљОЋОъОЎОаОЋ
ОЎОЕОаОЮ ОъОАОцОе ОћОЏОюОюОЋОф ОЕОю ОћОеОбОЎОЋОЪ ОЕОю ОћОцОЋОюОЎОаОЋОъОЎОаОЋОЎОЮ ОюОдОЋОеОЋОф ОаОЋОАОцОЋОф.
-
ОћОъОЋОаОЎОљОъОЋОаОЊ (moniamond)
-
ОћОЊОЎОљОъОЋОаОЊ (diamond)
-
ОћОўОеОЎОљОъОЋОаОЊОЎОЮ (triamond)
-
ОћОўОўОеОЎОъОЋОаОЊОЎОЮ (tetriamonds)
-
ОћОцОаОўОЎОљОъОЋОаОЊОЎОЮ
-
ОћОћОДОАОЎОљОъОЋОаОЊОЎОЮ
- ОћОћОДОАОљОЋОъОЎОаОЋОЎОЮ: ОдОЋОеОЋОф ОћОЉОаОЋОЎОЋОф ОъОЌОЎОЉОЋОе ОЎОЌОЊОЎОЋ ОЕОю ОъОЕОЋОЕОЎОЮ ОъОЕОЋОЏОюОюОЎОЮ.
 ОћОцОЋОюОЎОЊОюОфОЋОаОЎОЮ: ОћОъОЋОаОЋОЊОюОфОЋОЪ, ОЕОаОЎ ОћОЊОЎОЊОюОфОЋОаОЎОЮ ОЋОљОеОЉОбОф ОћОўОеОЎОЊОюОфОЋОаОЎОЮ
ОћОцОЋОюОЎОЊОюОфОЋОаОЎОЮ: ОћОъОЋОаОЋОЊОюОфОЋОЪ, ОЕОаОЎ ОћОЊОЎОЊОюОфОЋОаОЎОЮ ОЋОљОеОЉОбОф ОћОўОеОЎОЊОюОфОЋОаОЎОЮ
ОЉОЏОю ОћОдОЋОеОЋОф ОћОюОюОЋ ОћОЌОЎОЊОЋОф ОћОЉОАОЎОАОЎОЋОф ОбОЋОАОДОЋОф ОЉОеОЎОдОЋОцОЎОЮ ОЕОю ОћОъОЎОЕОЋОе ОЉОбОќОеОфОЪ, ОЋОЏОЪ ОЉОеОЎОдОЋОцОЎОЮ ОЕОю ОдОЋОеОЋОф ОАОцОдОЎОцОЎОЋОф ОЉОбОќОеОфОЪ.
ОеОљОЋ ОњОЮ
ОюОДОеОЎОљОћ ОаОЋОАОцОф
- Doris Schattschneider, "In Praise of Amateurs,"The Mathematical Gardner, D. Klarner (ed.). Belmont, CA: Wadsworth, 1981
ОДОЎОЕОЋОеОЎОЮ ОЌОЎОдОЋОаОЎОЎОЮ
ОћОбОеОЋОф ОЕОЋОюОЎОЎОЮ