קבוצה קומפקטית
|
Read other articles:
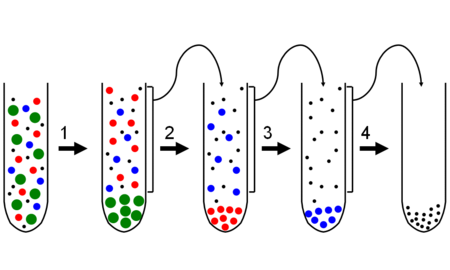
Peralatan distilasi fraksi menggunakan pendingin Liebig. Sebuah labu Erlenmeyer digunakan sebagai labu penampung. Di sini kepada distilasi dan kolom fraksi digabungkan menjadi satu. Sentrifugasi diferensial. Fraksionasi adalah proses pemisahan di mana sejumlah tertentu campuran (gas, padatan, cairan, suspensi, atau isotop) dipisahkan selama transisi fasa menjadi sejumlah kecil bagian (fraksi-fraksi), yang mana komposisinya bervariasi sesuai gradiennya. Fraksi-fraksi dikumpulkan berdasarkan pe...

Pembantaian SinjarBagian dari Serangan di Irak Utara (Agustus 2014) dan intervensi Amerika Serikat di Irak 2014Pesawat F/A-18C Hornet di atas kapal induk USS George H.W. Bush sebelum melancarkan serangan udara.Tanggal3–14 Agustus 2014(1 minggu dan 4 hari)LokasiŞingal (Sinjar), Provinsi Nineveh, IrakHasil Daulah Islamiyah merebut Sinjar[6] dan membantai 500 orang Yazidi;[7] Serangan udara Amerika Serikat menghentikan pengepungan Daulah Islamiyah atas[8] 50....

Halaman sampul karya Ishtori Haparchi Kaftor Vaferech, Venice 1549. Dalam buku cetak Ibrani pertama mengenai geografi Palestina, teridentifikasi 180 lokasi yang disebutkan dalam Alkitab dan sastra Talmud. Ishtori Haparchi (1280-1355) (juga Estori Haparchi, Nestorius ha-Parhi, Ashtori ha-Parhi; Ibrani: אשתורי הפרחיcode: he is deprecated ) adalah nama pena dokter, topografer, dan pengelana, Yahudi dari abad ke-14 Ishak HaKohen Ben Musa.[1] Biografi Ishtori Haparchi lahir di P...

State highway in southeastern Massachusetts, US Route 106Route 106 highlighted in redRoute informationMaintained by MassDOTLength34.31 mi[1] (55.22 km)Major junctionsWest end Route 1A in PlainvilleMajor intersections US 1 in Plainville Route 140 in Mansfield Route 24 in West Bridgewater East end Route 3A in Kingston LocationCountryUnited StatesStateMassachusettsCountiesNorfolk, Bristol, Plymouth Highway system Massachusetts State Highw...
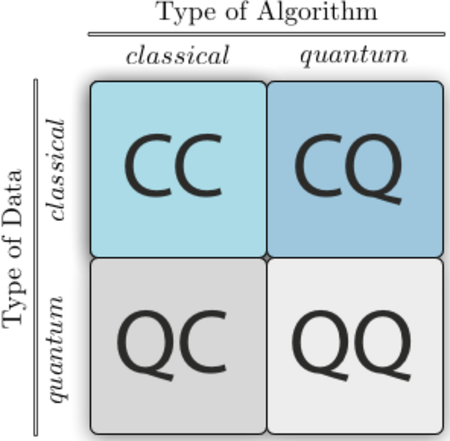
Interdisciplinary research area at the intersection of quantum physics and machine learning A major contributor to this article appears to have a close connection with its subject. It may require cleanup to comply with Wikipedia's content policies, particularly neutral point of view. Please discuss further on the talk page. (September 2018) (Learn how and when to remove this template message) This article may need to be rewritten to comply with Wikipedia's quality standards, as it is excessiv...

1981 film by Éric Rohmer The Aviator's WifeTheatrical release posterFrenchLa Femme de l'aviateur Directed byÉric RohmerWritten byÉric RohmerProduced byMargaret MénégozStarring Philippe Marlaud Marie Rivière Anne-Laure Meury Mathieu Carrière Philippe Caroit Haydée Caillot Mary Stephen Rosette Fabrice Luchini CinematographyBernard LuticEdited byCécile DecugisMusic byGeorges PratProductioncompanyLes Films du losangeDistributed byGaumontRelease date 4 March 1981 (1981-03-0...

American cultural historian Judith DupréBornProvidence, Rhode IslandNationalityAmericanOccupationAuthorWebsiteJudith Dupré Judith Dupré (born in Providence, Rhode Island)[1] is a writer, structural historian, and public speaker. She is the New York Times bestselling author of several works of narrative nonfiction on art, design, and architecture. She has been described as “a scholar with a novelist’s eye for detail and a journalist’s easy style.”[2] Life and career ...

Castle in Zanjan Province, Iran Soltaniyeh castleقلعه سلطانیهGeneral informationTypeCastleTown or citySoltaniyehCountry IranSoltaniyeh castle (Persian: قلعه سلطانیه) is a historical castle located in Soltaniyeh County in Zanjan Province, The longevity of this fortress dates back to the 1st millennium BC.[1][2] References ^ Encyclopaedia of the Iranian Architectural History. Cultural Heritage, Handicrafts and Tourism Organization of Iran. 15 February 2021....

Lake in the Northwest Territories, Canada Boyd LakeLocation within Northwest TerritoriesBoyd LakeLocationNorthwest TerritoriesCoordinates61°29′06″N 103°24′40″W / 61.4850°N 103.4111°W / 61.4850; -103.4111 (Boyd Lake)Basin countriesCanada Boyd Lake is a lake in the Northwest Territories, Canada.[1] Map See also List of lakes in the Northwest Territories Geography portalCanada portal References ^ Map of Boyd Lake, Canada, North America. Co...

此條目可能包含不适用或被曲解的引用资料,部分内容的准确性无法被证實。 (2023年1月5日)请协助校核其中的错误以改善这篇条目。详情请参见条目的讨论页。 各国相关 主題列表 索引 国内生产总值 石油储量 国防预算 武装部队(军事) 官方语言 人口統計 人口密度 生育率 出生率 死亡率 自杀率 谋杀率 失业率 储蓄率 识字率 出口额 进口额 煤产量 发电量 监禁率 死刑 国债 ...

Place in Normandy, FranceÎles Saint-MarcoufÎles Saint-Marcouf from the beach at RavenovilleÎles Saint-MarcoufLocation in NormandyShow map of NormandyÎles Saint-MarcoufÎles Saint-Marcouf (France)Show map of FranceCoordinates: 49°29′45″N 1°09′00″W / 49.49583°N 1.15000°W / 49.49583; -1.15000Country FranceRegionNormandy Îles Saint-Marcouf comprise two small uninhabited islands off the coast of Normandy, France. They lie in the Baie de la Seine region...

Ukrainian physicist Olexander SmakulaBorn9 September 1900Dobrovody, Austria-Hungary (today Ukraine)Died17 May 1983Auburn, Massachusetts, USAAlma materUniversity of GöttingenKnown foranti-reflective coatingScientific careerFieldsPhysicistInstitutionsOdessa UniversityCarl Zeiss AGMassachusetts Institute of TechnologyDoctoral advisorRobert Pohl Olexander Smakula (Ukrainian: Олександр Теодорович Смакула) (1900 in Dobrovody, Austria-Hungary, today Ukraine – 1...

Pour les articles homonymes, voir Denton. Cet article est une ébauche concernant une localité du Nebraska. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. DentonGéographiePays États-UnisÉtat NebraskaComté comté de LancasterSuperficie 0,32 km2 (2010)Surface en eau 0 %Altitude 380 mCoordonnées 40° 44′ 22″ N, 96° 50′ 42″ ODémographiePopulation 189 hab....

1899 short story collection by E. W. Hornung The Amateur Cracksman AuthorE. W. HornungLanguageEnglishSeriesA. J. RafflesGenreCrime fictionPublisherMethuen & Co. (UK)Scribner's (US)Publication date1899Publication placeUnited KingdomFollowed byThe Black Mask The Amateur Cracksman is an 1899 short story collection by E. W. Hornung. It was published in the UK by Methuen & Co., London, and in the US by Scribner's, New York.[1] Many later editions (T. Nelson & Sons, 1...

American media company This article is about the Cowles Company of Spokane, Washington. For other persons and entities named Cowles, see Cowles (disambiguation). Cowles CompanyCompany typePrivateIndustryPublishing, manufacturing, media, real estateFounded1894; 130 years ago (1894)FounderWilliam H. CowlesHeadquartersSpokane, Washington, U.S.Area servedSpokane, Washington, Spokane Valley, Washington, Coeur d'Alene, Idaho, Inland EmpireKey peopleElizabeth A. Cowles(Chair)W. Sta...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Februari 2023. Kosmos 1408Jenis misiSIGINTCOSPAR ID1982-092ASATCAT no.13552Durasi misi6 bulan (rencana) Properti wahanaWahana antariksaKosmos 1408Jenis wahana antariksaSIGINTBusTselina-DMassa luncur2.200 kg (4.900 pon) Awal misiTanggal luncur16 September 1...

У этого топонима есть и другие значения, см. Нав. КоммунаНавNaves 46°10′33″ с. ш. 3°06′36″ в. д.HGЯO Страна Франция Регион Овернь Департамент Алье Кантон Эбрёй Мэр Jean-Pierre Rogacki(2008–2014) История и география Площадь 8,13 км² Высота центра 296–433 м Часовой пояс UTC+1:00, летом UTC+2:00 ...

Oberengstringen Oberengstringen gemeinde de Suiza Escudo OberengstringenLocalización de Oberengstringen en SuizaPaís Suiza• Cantón Zúrich• Distrito DietikonUbicación 47°24′37″N 8°27′48″E / 47.410277777778, 8.4633333333333• Altitud 413 mSuperficie 2,13 km²Población[1] 6539 hab. (2014)• Densidad 3070 hab./km²Lengua AlemánCódigo postal 8102Sitio web Sitio web oficial[editar datos en ...

Brought the Heat BackSampul versi RemixSingel oleh Enhypendari album Romance: UntoldBahasaInggrisKoreaDirilis1 Agustus 2024 (2024-08-01)Direkam2024GenreK-popDurasi2:56Pencipta JHart Jesse Saint John Cirkut Yu Bin Hwang Danke Hitman Bang Inverness ProduserCirkutKronologi singel Enhypen XO (Only If You Say Yes) (2024) Brought the Heat Back (2024) Kronologi singel Ava Max My Oh My(2024) Brought the Heat Back(2024) Video musikBrought the Heat Back di YouTube Brought the Heat Back adalah...

Arthur MilleFonctionsPrésidentConseil de l'ordre du Grand Orient de France (d)1922-1925Augustin GérardArthur GroussierDéputé de l'Allier25 avril 1909 - 31 mai 1914BiographieNaissance 30 juillet 1854BeaupréauDécès 15 novembre 1942 (à 88 ans)6e arrondissement de LyonNom de naissance Arthur Victor MilleNationalité françaiseActivité Homme politiqueAutres informationsParti politique Section française de l'Internationale ouvrièremodifier - modifier le code - modifier Wikidata Arth...
![{\displaystyle [0,1]=\{x:0\leq x\leq 1\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/97c4c86068d567537f7eaaadd8356d9feca4668d)





























![{\displaystyle [-n,n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/89ffac59008711e9f5013abd9f65f23426f893b5)









