Ч‘ЧһЧӣЧ ЧҷЧ§ЧӘ Ч”Ч§Ч•Ч•Ч ЧҳЧҷЧқ, ЧӨЧ•ЧҳЧ ЧҰЧҷЧҗЧң Ч“ЧңЧӘЧҗ Ч”Ч•Чҗ Ч‘Ч•ЧЁ ЧӨЧ•ЧҳЧ ЧҰЧҷЧҗЧң Ч”ЧһЧӘЧ•ЧҗЧЁ ЧһЧӘЧһЧҳЧҷЧӘ ЧўЧң ЧҷЧ“Чҷ ЧӨЧ•Ч Ч§ЧҰЧҷЧҷЧӘ Ч“ЧңЧӘЧҗ Ч©Чң Ч“ЧҷЧЁЧҗЧ§ - ЧӨЧ•Ч Ч§ЧҰЧҷЧ” ЧһЧ•ЧӣЧңЧңЧӘ. ЧҗЧҷЧӣЧ•ЧӘЧҷЧӘ, Ч”ЧһЧ•Ч“Чң ЧһЧӘЧҗЧЁ ЧӨЧ•ЧҳЧ ЧҰЧҷЧҗЧң Ч©ЧўЧЁЧӣЧ• ЧҗЧӨЧЎ Ч‘ЧӣЧң ЧһЧ§Ч•Чқ, ЧңЧһЧўЧҳ Ч Ч§Ч•Ч“Ч” Ч‘Ч•Ч“Ч“ЧӘ Ч©Ч‘Ч” Ч”Ч•Чҗ ЧһЧ§Ч‘Чң ЧўЧЁЧҡ ЧҗЧҷЧ ЧЎЧ•ЧӨЧҷ. ЧһЧ•Ч“Чң Ч–Ч” ЧһЧ©ЧһЧ© ЧӣЧ“Чҷ ЧңЧӘЧҗЧЁ ЧӘЧЁЧ—ЧҷЧ©ЧҷЧқ Ч©Ч‘Ч”Чқ Ч—ЧңЧ§ЧҷЧ§ Ч—Ч•ЧӨЧ©Чҷ ЧңЧ Ч•Чў Ч‘Ч©Ч Чҷ ЧҗЧ–Ч•ЧЁЧҷЧқ Ч©Чң Ч”ЧһЧЁЧ—Ч‘ Ч‘ЧҷЧ ЧҷЧ”Чқ ЧһЧӨЧЁЧҷЧ“ ЧһЧ—ЧЎЧ•Чқ ЧӨЧ•ЧҳЧ ЧҰЧҷЧҗЧң ЧҰЧЁ Ч•Ч’Ч‘Ч•Ч” ЧһЧҗЧ•Ч“. ЧңЧ“Ч•Ч’ЧһЧ”, ЧҗЧңЧ§ЧҳЧЁЧ•Чҹ ЧҷЧӣЧ•Чң ЧңЧ Ч•Чў Ч‘Ч—Ч•ЧӨЧ©ЧҷЧ•ЧӘ ЧӣЧһЧўЧҳ ЧһЧ•Ч—ЧңЧҳЧӘ Ч‘Ч—Ч•ЧһЧЁ ЧһЧ•ЧңЧҷЧҡ, ЧӣЧҡ Ч©ЧҗЧқ Ч”ЧһЧ•ЧңЧҷЧҡ Ч‘Ч• Ч”Ч•Чҗ Ч Чў ЧҷЧ•ЧҰЧһЧ“ ЧңЧһЧ•ЧңЧҷЧҡ Ч©Ч Чҷ, Ч”ЧһЧһЧ©Ч§ Ч‘ЧҷЧ ЧҷЧ”Чқ ЧҷЧӨЧўЧң ЧўЧ‘Ч•ЧЁ Ч”ЧҗЧңЧ§ЧҳЧЁЧ•Чҹ ЧӣЧһЧ—ЧЎЧ•Чқ ЧӨЧ•ЧҳЧ ЧҰЧҷЧҗЧң Ч”ЧһЧӨЧЁЧҷЧ“ Ч‘ЧҷЧҹ ЧҗЧ–Ч•ЧЁЧҷЧқ Ч‘ЧўЧңЧҷ ЧӨЧ•ЧҳЧ ЧҰЧҷЧҗЧң Ч§Ч‘Ч•Чў - ЧһЧ—ЧЎЧ•Чқ Ч©ЧҷЧӣЧ•Чң ЧңЧ”ЧҷЧ•ЧӘ ЧһЧ§Ч•ЧЁЧ‘ ЧўЧң ЧҷЧ“Чҷ ЧӨЧ•Ч Ч§ЧҰЧҷЧҷЧӘ Ч“ЧңЧӘЧҗ. ЧӨЧ•ЧҳЧ ЧҰЧҷЧҗЧң Ч”Ч“ЧңЧӘЧҗ Ч”Ч•Чҗ Ч’Ч‘Ч•Чң Ч©Чң Ч‘Ч•ЧЁ ЧӨЧ•ЧҳЧ ЧҰЧҷЧҗЧң ЧЎЧ•ЧӨЧҷ, Ч•Ч ЧҷЧӘЧҹ ЧңЧ§Ч‘ЧңЧ• ЧһЧ‘Ч•ЧЁ Ч”ЧӨЧ•ЧҳЧ ЧҰЧҷЧҗЧң Ч”ЧЎЧ•ЧӨЧҷ ЧҗЧқ Ч©Ч•ЧһЧЁЧҷЧқ ЧўЧң ЧһЧӣЧӨЧңЧӘ ЧўЧ•ЧһЧ§ (ЧҗЧ• Ч’Ч•Ч‘Ч”) Ч”Ч‘Ч•ЧЁ Ч•ЧЁЧ•Ч—Ч‘Ч• ЧўЧң ЧўЧЁЧҡ Ч§Ч‘Ч•Чў ЧӣЧҗЧ©ЧЁ ЧһЧ§ЧҳЧҷЧ ЧҷЧқ ЧҗЧӘ Ч”ЧЁЧ•Ч—Ч‘ Ч‘Ч”Ч“ЧЁЧ’Ч” ЧңЧҗЧӨЧЎ.
ЧӨЧ•ЧҳЧ ЧҰЧҷЧҗЧң Ч“ЧңЧӘЧҗ ЧҷЧ—ЧҷЧ“
![]()
ЧһЧ©Ч•Ч•ЧҗЧӘ Ч©ЧЁЧ“ЧҷЧ Ч’ЧЁ Ч”Ч‘ЧңЧӘЧҷ ЧӘЧңЧ•ЧҷЧ” Ч‘Ч–ЧһЧҹ ЧңЧӨЧ•Ч Ч§ЧҰЧҷЧҷЧӘ Ч”Ч’Чң (ПҲ(x Ч©Чң Ч—ЧңЧ§ЧҷЧ§ Ч‘ЧһЧһЧ“ ЧҗЧ—Ч“ Ч‘ЧӨЧ•ЧҳЧ ЧҰЧҷЧҗЧң (V(x Ч”ЧҷЧҗ:

ЧӣЧҗЧ©ЧЁ Д§ Ч”Ч•Чҗ Ч§Ч‘Ч•Чў ЧӨЧңЧ Ч§ Ч”ЧһЧҰЧ•ЧһЧҰЧқ Ч•-E Ч”ЧҷЧҗ Ч”ЧҗЧ ЧЁЧ’ЧҷЧ” Ч©Чң Ч”Ч—ЧңЧ§ЧҷЧ§.
ЧӨЧ•ЧҳЧ ЧҰЧҷЧҗЧң Ч”Ч“ЧңЧӘЧҗ Ч”Ч•Чҗ Ч”ЧӨЧ•ЧҳЧ ЧҰЧҷЧҗЧң

ЧӣЧҗЧ©ЧЁ (Оҙ(x Ч”Ч•Чҗ ЧӨЧ•Ч Ч§ЧҰЧҷЧҷЧӘ Ч“ЧңЧӘЧҗ Ч©Чң Ч“ЧҷЧЁЧҗЧ§.
Ч”Ч•Чҗ ЧҷЧҷЧ§ЧЁЧҗ Ч‘Ч•ЧЁ ЧӨЧ•ЧҳЧ ЧҰЧҷЧҗЧң Ч“ЧңЧӘЧҗ ЧҗЧқ О» Ч©ЧңЧҷЧңЧҷ Ч•ЧһЧ—ЧЎЧ•Чқ ЧӨЧ•ЧҳЧ ЧҰЧҷЧҗЧң Ч“ЧңЧӘЧҗ ЧҗЧқ О» Ч—ЧҷЧ•Ч‘Чҷ.
ЧӨЧӘЧЁЧ•Чҹ ЧһЧ©Ч•Ч•ЧҗЧӘ Ч©ЧЁЧ“ЧҷЧ Ч’ЧЁ
Ч”ЧӨЧ•ЧҳЧ ЧҰЧҷЧҗЧң ЧһЧӨЧҰЧң ЧҗЧӘ Ч”ЧһЧЁЧ—Ч‘ ЧңЧ©Ч Чҷ Ч—ЧңЧ§ЧҷЧқ (x < 0 Ч•-x > 0). Ч‘ЧӣЧң ЧҗЧ—Ч“ ЧһЧ”Ч—ЧңЧ§ЧҷЧқ Ч”ЧҗЧңЧ• Ч”ЧҗЧ ЧЁЧ’ЧҷЧ” Ч”ЧӨЧ•ЧҳЧ ЧҰЧҷЧҗЧңЧҷЧӘ Ч”ЧҷЧҗ ЧҗЧӨЧЎ, Ч•ЧһЧ©Ч•Ч•ЧҗЧӘ Ч©ЧЁЧ“ЧҷЧ Ч’ЧЁ ЧһЧҰЧ•ЧһЧҰЧһЧӘ ЧңЧһЧ©Ч•Ч•ЧҗЧ”

Ч–Ч•Ч”Чҷ ЧһЧ©Ч•Ч•ЧҗЧ” Ч“ЧҷЧӨЧЁЧ ЧҰЧҷЧҗЧңЧҷЧӘ ЧңЧҷЧ ЧҷЧҗЧЁЧҷЧӘ ЧўЧқ ЧһЧ§Ч“ЧһЧҷЧқ Ч§Ч‘Ч•ЧўЧҷЧқ ЧҗЧ©ЧЁ ЧӨЧӘЧЁЧ•Ч Ч•ЧӘЧҷЧ” Ч”Чқ ЧҰЧҷЧЁЧ•ЧӨЧҷЧқ ЧңЧҷЧ ЧҷЧҗЧЁЧҷЧҷЧқ Ч©Чң eikx Ч•-eвҲ’ikx, ЧӣЧҗЧ©ЧЁ ЧһЧЎЧӨЧЁ Ч”Ч’Чң
k Ч§Ч©Ч•ЧЁ ЧңЧҗЧ ЧЁЧ’ЧҷЧ” ЧўЧң ЧҷЧ“Чҷ:
 .
.
Ч‘ЧҗЧ•ЧӨЧҹ ЧӣЧңЧңЧҷ, ЧўЧ§Ч‘ Ч Ч•ЧӣЧ—Ч•ЧӘЧ• Ч©Чң ЧӨЧ•ЧҳЧ ЧҰЧҷЧҗЧң Ч”Ч“ЧңЧӘЧҗ Ч‘ЧЁЧҗЧ©ЧҷЧӘ, ЧһЧ§Ч“ЧһЧҷ Ч”ЧӨЧӘЧЁЧ•Чҹ ЧңЧҗ Ч—ЧҷЧҷЧ‘ЧҷЧқ ЧңЧ”ЧҷЧ•ЧӘ Ч–Ч”ЧҷЧқ Ч‘Ч©Ч Чҷ Ч—ЧҰЧҗЧҷ Ч”ЧһЧЁЧ—Ч‘:

ЧӣЧҗЧ©ЧЁ, Ч‘ЧһЧ§ЧЁЧ” Ч©Чң ЧҗЧ ЧЁЧ’ЧҷЧ•ЧӘ Ч—ЧҷЧ•Ч‘ЧҷЧ•ЧӘ (k ЧһЧһЧ©Чҷ), eikx ЧһЧҷЧҷЧҰЧ’ Ч’Чң Ч©ЧһЧӘЧ§Ч“Чқ ЧҷЧһЧҷЧ Ч”, Ч•-eвҲ’ikx ЧһЧҷЧҷЧҰЧ’ Ч’Чң Ч©ЧһЧӘЧ§Ч“Чқ Ч©ЧһЧҗЧңЧ”.
Ч ЧҷЧӘЧҹ ЧңЧ§Ч‘Чң Ч§Ч©ЧЁ ЧЁЧҗЧ©Ч•Чҹ Ч‘ЧҷЧҹ Ч”ЧһЧ§Ч“ЧһЧҷЧқ Ч‘ЧҗЧһЧҰЧўЧ•ЧӘ Ч”ЧӣЧӨЧӨЧӘ ЧӨЧ•Ч Ч§ЧҰЧҷЧҷЧӘ Ч”Ч’Чң ЧңЧӘЧ ЧҗЧҷ Ч”ЧЁЧҰЧҷЧӨЧ•ЧӘ Ч‘ЧЁЧҗЧ©ЧҷЧӘ, ЧӣЧңЧ•ЧһЧЁ:

Ч§Ч©ЧЁ Ч©Ч Чҷ ЧһЧӘЧ§Ч‘Чң ЧһЧҗЧӨЧҷЧ•Чҹ Ч”Ч§ЧӨЧҷЧҰЧ” Ч‘Ч Ч’Ч–ЧЁЧӘ Ч©Чң ЧӨЧ•Ч Ч§ЧҰЧҷЧҷЧӘ Ч”Ч’Чң Ч‘ЧЁЧҗЧ©ЧҷЧӘ. ЧңЧӣЧҗЧ•ЧЁЧ” Ч ЧҷЧӘЧҹ ЧңЧҳЧўЧ•Чҹ Ч’Чқ ЧңЧ’Ч–ЧҷЧЁЧ•ЧӘ ЧӨЧ•Ч Ч§ЧҰЧҷЧҷЧӘ Ч”Ч’Чң Ч‘ЧЁЧҗЧ©ЧҷЧӘ, ЧҗЧҡ ЧҷЧ© ЧңЧ–ЧӣЧ•ЧЁ Ч©ЧҗЧһЧ Чқ ЧӨЧ•ЧҳЧ ЧҰЧҷЧҗЧң Ч”Ч“ЧңЧӘЧҗ Ч”Ч•Чҗ Ч’Ч‘Ч•Чң Ч©Чң ЧһЧңЧ‘Ч ЧҷЧқ Ч”Ч ЧўЧ©ЧҷЧқ ЧҰЧЁЧҷЧқ ЧҷЧ•ЧӘЧЁ Ч•ЧҷЧ•ЧӘЧЁ, ЧҗЧҡ Ч”Ч•Чҗ Ч’Чқ Ч’Ч‘Ч•Чң Ч©Чң ЧһЧңЧ‘Ч ЧҷЧқ Ч”Ч ЧўЧ©ЧҷЧқ Ч’Ч‘Ч•Ч”ЧҷЧқ ЧҷЧ•ЧӘЧЁ Ч•ЧҷЧ•ЧӘЧЁ (ЧӨЧ•Ч Ч§ЧҰЧҷЧҷЧӘ Ч“ЧңЧӘЧҗ ЧһЧӘЧ§Ч‘ЧңЧӘ ЧһЧЎЧ“ЧЁЧӘ ЧһЧңЧ‘Ч ЧҷЧқ Ч‘ЧўЧңЧҷ Ч©ЧҳЧ— Ч§Ч‘Ч•Чў), ЧӣЧҡ Ч©ЧҗЧқ Ч”Ч—ЧңЧ§ЧҷЧ§ ЧһЧһЧ Ч”ЧЁ Ч“ЧЁЧҡ ЧһЧ—ЧЎЧ•Чқ Ч”ЧӨЧ•ЧҳЧ ЧҰЧҷЧҗЧң ЧҗЧ– Ч‘ЧҗЧ–Ч•ЧЁ Ч”ЧһЧңЧ‘Чҹ Ч”Ч’Ч‘Ч•ЧңЧҷ ЧһЧЎЧӨЧЁ Ч”Ч’Чң Ч©ЧңЧ• ЧҷЧ”ЧҷЧ” ЧҗЧҷЧ ЧЎЧ•ЧӨЧҷ - ЧңЧӣЧҹ ЧўЧ“ЧҷЧҷЧҹ ЧһЧӘЧ§Ч‘Чң Ч”ЧӨЧЁЧ© ЧһЧ•ЧӨЧў.
ЧӣЧ“Чҷ ЧңЧ§Ч‘Чң ЧҗЧӘ Ч”Ч§ЧӨЧҷЧҰЧ” Ч‘Ч Ч’Ч–ЧЁЧӘ Ч Ч‘ЧҰЧў ЧҗЧҷЧ ЧҳЧ’ЧЁЧҰЧҷЧ” Ч©Чң ЧһЧ©Ч•Ч•ЧҗЧӘ Ч©ЧЁЧ“ЧҷЧ Ч’ЧЁ ЧһЧЎЧ‘ЧҷЧ‘ Чң- x = 0 ЧўЧң ЧӨЧ Чҷ Ч”ЧҗЧҷЧ ЧҳЧЁЧ•Ч•Чң [Оө,+Оө-]:

Ч‘Ч’Ч‘Ч•Чң Ч©Ч‘Ч• ОөвҶ’ 0, ЧҗЧ’ЧЈ ЧҷЧһЧҷЧҹ Ч©Чң Ч”ЧһЧ©Ч•Ч•ЧҗЧ” Ч”Ч–ЧҗЧӘ ЧһЧӘЧҗЧӨЧЎ, Ч•ЧҗЧ’ЧЈ Ч©ЧһЧҗЧң Ч”Ч•ЧӨЧҡ Чң-:
![{\displaystyle \textstyle -{\frac {\hbar ^{2}}{2m}}[\psi '_{R}(0)-\psi '_{L}(0)]+\lambda \psi (0),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4303c79a049714dd9f1cde212495da54ff8f6d86)
Ч–ЧҗЧӘ ЧһЧӨЧ Чҷ Ч©-:
![{\displaystyle \int _{-\epsilon }^{+\epsilon }\psi ''(x)\,dx=[\psi '({+\epsilon })-\psi '({-\epsilon })].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9b0c5ea0e70e99d056942b7806012a5c2afd96bc)
ЧңЧӨЧҷЧӣЧҡ ЧһЧ§Ч‘ЧңЧҷЧқ:

ЧңЧЎЧҷЧӣЧ•Чқ, ЧӘЧ ЧҗЧҷ Ч”Ч©ЧӨЧ” ЧһЧЎЧӨЧ§ЧҷЧқ ЧҗЧӘ Ч”ЧҗЧҷЧңЧ•ЧҰЧҷЧқ Ч”Ч‘ЧҗЧҷЧқ ЧўЧң Ч”ЧһЧ§Ч“ЧһЧҷЧқ:

ЧһЧҰЧ‘ Ч§Ч©Ч•ЧЁ (E < 0)
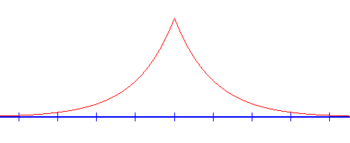 Ч”Ч’ЧЁЧЈ Ч©Чң ЧӨЧ•Ч Ч§ЧҰЧҷЧҷЧӘ Ч”Ч’Чң Ч©Чң Ч”ЧһЧҰЧ‘ Ч”Ч§Ч©Ч•ЧЁ ЧңЧӨЧ•ЧҳЧ ЧҰЧҷЧҗЧң Ч“ЧңЧӘЧҗ Ч”Ч•Чҗ ЧЁЧҰЧҷЧЈ Ч‘ЧӣЧң ЧһЧ§Ч•Чқ, ЧҗЧҡ Ч Ч’Ч–ЧЁЧӘЧ• ЧҗЧҷЧ Ч” ЧһЧ•Ч’Ч“ЧЁЧӘ Ч‘-x=0.
Ч”Ч’ЧЁЧЈ Ч©Чң ЧӨЧ•Ч Ч§ЧҰЧҷЧҷЧӘ Ч”Ч’Чң Ч©Чң Ч”ЧһЧҰЧ‘ Ч”Ч§Ч©Ч•ЧЁ ЧңЧӨЧ•ЧҳЧ ЧҰЧҷЧҗЧң Ч“ЧңЧӘЧҗ Ч”Ч•Чҗ ЧЁЧҰЧҷЧЈ Ч‘ЧӣЧң ЧһЧ§Ч•Чқ, ЧҗЧҡ Ч Ч’Ч–ЧЁЧӘЧ• ЧҗЧҷЧ Ч” ЧһЧ•Ч’Ч“ЧЁЧӘ Ч‘-x=0.
Ч‘ЧӣЧң ЧӨЧ•ЧҳЧ ЧҰЧҷЧҗЧң ЧһЧ•Ч©Чҡ Ч—Ч“ЦҫЧһЧһЧ“Чҷ ЧҷЧ”ЧҷЧ” ЧһЧҰЧ‘ Ч§Ч©Ч•ЧЁ. ЧӣЧ“Чҷ ЧңЧһЧҰЧ•Чҗ ЧҗЧӘ Ч”ЧҗЧ ЧЁЧ’ЧҷЧ” Ч©ЧңЧ•, ЧҷЧ© ЧңЧ©ЧҷЧқ ЧңЧ‘ Ч©Ч‘ЧўЧ‘Ч•ЧЁ E<0 ЧһЧӘЧ§Ч‘Чң  ЧһЧ“Ч•ЧһЧ” Ч•ЧӨЧ•Ч Ч§ЧҰЧҷЧ•ЧӘ Ч”Ч’Чң ЧҗЧ©ЧЁ Ч”ЧҷЧ• ЧҗЧ•ЧЎЧҰЧҷЧңЧҳЧ•ЧЁЧҷЧ•ЧӘ Ч‘ЧўЧ‘Ч•ЧЁ ЧҗЧ ЧЁЧ’ЧҷЧ•ЧӘ Ч—ЧҷЧ•Ч‘ЧҷЧ•ЧӘ Ч‘Ч—ЧҷЧ©Ч•Ч‘ Ч©ЧһЧ§Ч•Ч“Чқ, Ч”Чҹ ЧӣЧўЧӘ ЧһЧўЧЁЧҷЧӣЧҷЧ•ЧӘ Ч“Ч•ЧўЧӣЧ•ЧӘ ЧҗЧ• ЧўЧ•ЧңЧ•ЧӘ ЧӣЧӨЧ•Ч Ч§ЧҰЧҷЧ” Ч©Чң x (ЧЁЧҗЧ• ЧҗЧҷЧ•ЧЁ). Ч”Ч“ЧЁЧҷЧ©Ч” Ч©ЧӨЧ•Ч Ч§ЧҰЧҷЧ•ЧӘ Ч”Ч’Чң ЧҗЧҷЧ Чҹ ЧһЧӘЧ‘Ч“ЧЁЧ•ЧӘ Ч‘ЧҗЧҷЧ ЧЎЧ•ЧЈ Ч’Ч•ЧЁЧЁЧӘ Ч”ЧӘЧҗЧӨЧЎЧ•ЧӘ Ч©Чң Ч”ЧҗЧ§ЧЎЧӨЧ•Ч Ч ЧҳЧҷЧқ Ч”ЧһЧӘЧ‘Ч“ЧЁЧҷЧқ, ЧӣЧҡ Ч©ЧӨЧ•Ч Ч§ЧҰЧҷЧҷЧӘ Ч”Ч’Чң Ч”ЧһЧӘЧ§Ч‘ЧңЧӘ Ч”ЧҷЧҗ:
ЧһЧ“Ч•ЧһЧ” Ч•ЧӨЧ•Ч Ч§ЧҰЧҷЧ•ЧӘ Ч”Ч’Чң ЧҗЧ©ЧЁ Ч”ЧҷЧ• ЧҗЧ•ЧЎЧҰЧҷЧңЧҳЧ•ЧЁЧҷЧ•ЧӘ Ч‘ЧўЧ‘Ч•ЧЁ ЧҗЧ ЧЁЧ’ЧҷЧ•ЧӘ Ч—ЧҷЧ•Ч‘ЧҷЧ•ЧӘ Ч‘Ч—ЧҷЧ©Ч•Ч‘ Ч©ЧһЧ§Ч•Ч“Чқ, Ч”Чҹ ЧӣЧўЧӘ ЧһЧўЧЁЧҷЧӣЧҷЧ•ЧӘ Ч“Ч•ЧўЧӣЧ•ЧӘ ЧҗЧ• ЧўЧ•ЧңЧ•ЧӘ ЧӣЧӨЧ•Ч Ч§ЧҰЧҷЧ” Ч©Чң x (ЧЁЧҗЧ• ЧҗЧҷЧ•ЧЁ). Ч”Ч“ЧЁЧҷЧ©Ч” Ч©ЧӨЧ•Ч Ч§ЧҰЧҷЧ•ЧӘ Ч”Ч’Чң ЧҗЧҷЧ Чҹ ЧһЧӘЧ‘Ч“ЧЁЧ•ЧӘ Ч‘ЧҗЧҷЧ ЧЎЧ•ЧЈ Ч’Ч•ЧЁЧЁЧӘ Ч”ЧӘЧҗЧӨЧЎЧ•ЧӘ Ч©Чң Ч”ЧҗЧ§ЧЎЧӨЧ•Ч Ч ЧҳЧҷЧқ Ч”ЧһЧӘЧ‘Ч“ЧЁЧҷЧқ, ЧӣЧҡ Ч©ЧӨЧ•Ч Ч§ЧҰЧҷЧҷЧӘ Ч”Ч’Чң Ч”ЧһЧӘЧ§Ч‘ЧңЧӘ Ч”ЧҷЧҗ:

ЧһЧӘЧ ЧҗЧҷ Ч”Ч©ЧӨЧ” Ч•ЧӘЧ ЧҗЧҷ Ч”Ч ЧЁЧһЧ•Чң Ч Ч•Ч‘Чў Ч©-:

ЧӣЧңЧ•ЧһЧЁ ЧһЧ§Ч‘ЧңЧҷЧқ Ч©ЧһЧҰЧ‘ Ч§Ч©Ч•ЧЁ ЧҷЧӣЧ•Чң ЧңЧ”ЧӘЧ§ЧҷЧҷЧқ ЧЁЧ§ ЧўЧ‘Ч•ЧЁ Ч‘Ч•ЧЁ (О» Ч—ЧҷЧҷЧ‘ ЧңЧ”ЧҷЧ•ЧӘ Ч©ЧңЧҷЧңЧҷ) Ч•ЧңЧҗ ЧўЧ‘Ч•ЧЁ ЧһЧ—ЧЎЧ•Чқ. ЧҳЧЁЧ ЧЎЧӨЧ•ЧЁЧқ ЧӨЧ•ЧЁЧҷЧҷЧ” Ч©Чң ЧӨЧ•Ч Ч§ЧҰЧҷЧҷЧӘ Ч”Ч’Чң Ч”Ч–ЧҗЧӘ Ч”Ч•Чҗ Ч”ЧӘЧӨЧңЧ’Ч•ЧӘ Ч§Ч•Ч©Чҷ.
Ч‘Ч©Ч•Ч Ч” ЧһЧ”ЧЎЧҷЧҳЧ•ЧҗЧҰЧҷЧ” Ч‘Ч‘Ч•ЧЁ ЧӨЧ•ЧҳЧ ЧҰЧҷЧҗЧң ЧЎЧ•ЧӨЧҷ, Ч‘Ч‘Ч•ЧЁ Ч“ЧңЧӘЧҗ ЧӘЧһЧҷЧ“ ЧҷЧ© ЧЁЧ§ ЧһЧҰЧ‘ Ч§Ч©Ч•ЧЁ ЧҗЧ—Ч“, Ч•Ч”ЧҗЧ ЧЁЧ’ЧҷЧ” Ч©Чң Ч”ЧһЧҰЧ‘ Ч”Ч§Ч©Ч•ЧЁ Ч Ч’Ч–ЧЁЧӘ ЧһЧ”Ч§Ч‘Ч•ЧўЧҷЧқ Ч©Чң Ч”Ч–Ч Ч‘Ч•ЧӘ Ч”ЧҗЧ§ЧЎЧӨЧ•Ч Ч ЧҰЧҷЧҗЧңЧҷЧҷЧқ:

ЧӨЧҷЧ–Ч•ЧЁ (E > 0)
 Ч”ЧЎЧӘЧ‘ЧЁЧ•ЧӘ Ч”ЧўЧ‘ЧЁЧ” (T) Ч•Ч”Ч—Ч–ЧЁЧ” (R) ЧһЧӨЧ•ЧҳЧ ЧҰЧҷЧҗЧң Ч“ЧңЧӘЧҗ. Ч”ЧҗЧ ЧЁЧ’ЧҷЧ” E > 0 Ч”ЧҷЧҗ Ч‘ЧҷЧ—ЧҷЧ“Ч•ЧӘ Ч©Чң
Ч”ЧЎЧӘЧ‘ЧЁЧ•ЧӘ Ч”ЧўЧ‘ЧЁЧ” (T) Ч•Ч”Ч—Ч–ЧЁЧ” (R) ЧһЧӨЧ•ЧҳЧ ЧҰЧҷЧҗЧң Ч“ЧңЧӘЧҗ. Ч”ЧҗЧ ЧЁЧ’ЧҷЧ” E > 0 Ч”ЧҷЧҗ Ч‘ЧҷЧ—ЧҷЧ“Ч•ЧӘ Ч©Чң  . Ч‘ЧһЧ§Ч•Ч•Ч§Ч•: Ч”Ч”ЧӘЧ Ч”Ч’Ч•ЧӘ Ч”Ч§ЧңЧҗЧЎЧҷЧӘ. Ч‘ЧһЧ•Ч“Ч’Ч©: Ч”Ч”ЧӘЧ Ч”Ч’Ч•ЧӘ Ч§Ч•Ч•Ч ЧҳЧҷЧӘ.
. Ч‘ЧһЧ§Ч•Ч•Ч§Ч•: Ч”Ч”ЧӘЧ Ч”Ч’Ч•ЧӘ Ч”Ч§ЧңЧҗЧЎЧҷЧӘ. Ч‘ЧһЧ•Ч“Ч’Ч©: Ч”Ч”ЧӘЧ Ч”Ч’Ч•ЧӘ Ч§Ч•Ч•Ч ЧҳЧҷЧӘ.
Ч‘ЧўЧ‘Ч•ЧЁ ЧҗЧ ЧЁЧ’ЧҷЧ•ЧӘ Ч—ЧҷЧ•Ч‘ЧҷЧ•ЧӘ, Ч”Ч—ЧңЧ§ЧҷЧ§ Ч—Ч•ЧӨЧ©Чҷ ЧңЧ Ч•Чў Ч‘ЧӣЧң ЧҗЧ—Ч“ ЧһЧ—ЧҰЧҗЧҷ Ч”ЧһЧЁЧ—Ч‘, ЧҗЧҡ Ч”Ч•Чҗ ЧўЧ©Ч•Чҷ ЧңЧ”ЧҷЧ•ЧӘ ЧһЧӨЧ•Ч–ЧЁ ЧһЧӨЧ•ЧҳЧ ЧҰЧҷЧҗЧң Ч”Ч“ЧңЧӘЧҗ Ч‘ЧЁЧҗЧ©ЧҷЧӘ.
ЧҗЧӘ Ч”ЧһЧ§ЧЁЧ” Ч”Ч§Ч•Ч•Ч ЧҳЧҷ Ч ЧҷЧӘЧҹ ЧңЧ—Ч§Ч•ЧЁ Ч‘ЧҗЧ•ЧӨЧҹ Ч”Ч‘Чҗ: Ч—ЧңЧ§ЧҷЧ§ ЧһЧӘЧ§ЧЁЧ‘ ЧӨЧ•Ч’Чў Ч‘ЧһЧ—ЧЎЧ•Чқ ЧһЧҰЧ“ Ч©ЧһЧҗЧң (Ar); Ч”Ч•Чҗ ЧўЧ©Ч•Чҷ ЧңЧ”ЧҷЧ•ЧӘ ЧһЧ•Ч—Ч–ЧЁ (Al) ЧҗЧ• ЧһЧ•ЧўЧ‘ЧЁ (Br). ЧӣЧ“Чҷ ЧңЧһЧҰЧ•Чҗ ЧҗЧӘ Ч”ЧҗЧһЧӨЧңЧҷЧҳЧ•Ч“Ч” Ч”ЧһЧ•Ч—Ч–ЧЁЧӘ Ч•Ч”ЧһЧ•ЧўЧ‘ЧЁЧӘ Ч‘ЧўЧ‘Ч•ЧЁ ЧӨЧ’ЧҷЧўЧ” ЧһЧҰЧ“ Ч©ЧһЧҗЧң, Ч ЧҰЧҷЧ‘ Ч‘ЧһЧ©Ч•Ч•ЧҗЧ•ЧӘ ЧңЧўЧҷЧң Ar = 1 (Ч—ЧңЧ§ЧҷЧ§ ЧһЧ’ЧҷЧў), Al = r (Ч”Ч—Ч–ЧЁЧ”), Bl = 0 (ЧҗЧЈ Ч—ЧңЧ§ЧҷЧ§ ЧңЧҗ ЧһЧ’ЧҷЧў ЧһЧҰЧ“ ЧҷЧһЧҷЧҹ) Ч•-Br = t (Ч”ЧўЧ‘ЧЁЧ”), Ч•Ч ЧӨЧӘЧ•ЧЁ Ч‘ЧўЧ‘Ч•ЧЁ r Ч•-t. Ч”ЧӘЧ•ЧҰЧҗЧ” Ч”ЧһЧӘЧ§Ч‘ЧңЧӘ Ч”ЧҷЧҗ:


ЧһЧ§Ч“Чқ Ч”Ч”ЧўЧ‘ЧЁЧ” Ч”Ч•Чҗ ЧһЧЁЧ•ЧӣЧ‘ ЧӣЧҷ Ч‘Ч Ч•ЧЎЧЈ ЧўЧң Ч”Ч”Ч‘Ч“Чң Ч‘ЧҷЧҹ ЧһЧ©ЧЁЧўЧӘ ЧӨЧ•Ч Ч§ЧҰЧҷЧҷЧӘ Ч”Ч’Чң Ч”ЧһЧ•ЧўЧ‘ЧЁЧӘ ЧңЧўЧ•ЧһЧӘ Ч–Ч• Ч”ЧӨЧ•Ч’ЧўЧӘ, ЧҷЧ©Ч Ч• Ч’Чқ Ч©ЧҷЧ Ч•Чҷ ЧһЧ•ЧӨЧў Ч”ЧһЧ§Ч•Ч©ЧЁ ЧңЧӨЧ•ЧҳЧ ЧҰЧҷЧҗЧң.
ЧҗЧ•Ч“Ч•ЧӘ ЧңЧЎЧҷЧһЧҳЧЁЧҷЧҷЧӘ Ч”ЧЁЧҗЧҷ Ч©Чң Ч”ЧһЧ•Ч“Чң, Ч”ЧҗЧһЧӨЧңЧҷЧҳЧ•Ч“Ч•ЧӘ Ч©Чң Ч”Ч’Чң Ч”ЧӨЧ•Ч’Чў ЧһЧҷЧһЧҷЧҹ Ч–Ч”Ч•ЧӘ ЧңЧҗЧңЧ• Ч©ЧһЧ©ЧһЧҗЧң. Ч”ЧӘЧ•ЧҰЧҗЧ” Ч©ЧһЧӘЧ§Ч‘ЧңЧӘ Ч”ЧҷЧҗ Ч©ЧҷЧ© Ч”ЧЎЧӘЧ‘ЧЁЧ•ЧӘ Ч’Ч“Ч•ЧңЧ” ЧһЧҗЧӨЧЎ

Ч©Ч”Ч—ЧңЧ§ЧҷЧ§ ЧҷЧ•Ч—Ч–ЧЁ. Ч”ЧЎЧҷЧӣЧ•Чҷ ЧңЧ”Ч—Ч–ЧЁЧ” Ч–ЧҗЧӘ ЧҗЧҷЧ Ч• ЧӘЧңЧ•Чҷ Ч‘ЧЎЧҷЧһЧҹ Ч©Чң О», ЧӣЧңЧ•ЧһЧЁ, ЧңЧ‘Ч•ЧЁ ЧҷЧ© ЧҗЧ•ЧӘЧ• ЧЎЧҷЧӣЧ•Чҷ ЧңЧӨЧ–ЧЁ ЧҗЧӘ Ч”Ч—ЧңЧ§ЧҷЧ§ ЧӣЧһЧ• ЧңЧһЧ—ЧЎЧ•Чқ. Ч–Ч”Ч• Ч”Ч‘Ч“Чң ЧһЧ©ЧһЧўЧ•ЧӘЧҷ ЧһЧ”ЧһЧӣЧ ЧҷЧ§Ч” Ч”Ч§ЧңЧҗЧЎЧҷЧӘ, Ч©Ч‘Ч” Ч”ЧЎЧӘЧ‘ЧЁЧ•ЧӘ Ч”Ч”Ч—Ч–ЧЁЧ” ЧӘЧ”ЧҷЧ” 1 ЧўЧ‘Ч•ЧЁ ЧһЧ—ЧЎЧ•Чқ (Ч”Ч—ЧңЧ§ЧҷЧ§ ЧӨЧ©Ч•Чҳ ЧһЧ§ЧӨЧҘ Ч—Ч–ЧЁЧ”) Ч•-0 ЧўЧ‘Ч•ЧЁ Ч‘Ч•ЧЁ (Ч”Ч—ЧңЧ§ЧҷЧ§ Ч—Ч•ЧңЧЈ Ч“ЧЁЧҡ Ч”Ч‘Ч•ЧЁ Ч‘ЧҗЧҷЧҹ ЧһЧӨЧЁЧҷЧў).
ЧңЧЎЧҷЧӣЧ•Чқ, Ч”ЧЎЧӘЧ‘ЧЁЧ•ЧӘ Ч”ЧһЧўЧ‘ЧЁ Ч”ЧҷЧҗ:
 .
.
Ч”Ч“Ч’Ч©ЧҷЧқ Ч•ЧҷЧҷЧ©Ч•ЧһЧҷЧқ
Ч”Ч—ЧҷЧ©Ч•Ч‘ ЧңЧўЧҷЧң ЧўЧ©Ч•Чҷ ЧңЧ”ЧҷЧЁЧҗЧ•ЧӘ Ч‘ЧӘЧ—ЧҷЧңЧ” ЧӣЧ”ЧӨЧ©ЧҳЧ” Ч—ЧЎЧЁЧӘ Ч©ЧҷЧһЧ•Ч©. ЧҗЧЈ ЧўЧң ЧӨЧҷ ЧӣЧҹ, Ч”Ч•Чҗ Ч”Ч•ЧӣЧҷЧ— ЧҗЧӘ ЧўЧҰЧһЧ• ЧӣЧһЧ•Ч“Чң ЧһЧӘЧҗЧҷЧқ ЧңЧһЧ’Ч•Ч•Чҹ ЧһЧўЧЁЧӣЧ•ЧӘ ЧӨЧҷЧ–ЧҷЧ§ЧңЧҷЧ•ЧӘ ЧҗЧһЧҷЧӘЧҷЧ•ЧӘ.
Ч“Ч•Ч’ЧһЧ” ЧҗЧ—ЧӘ ЧӣЧ–ЧҗЧӘ Ч Ч•Ч’ЧўЧӘ ЧңЧһЧһЧ©Ч§ЧҷЧқ Ч©Ч‘ЧҷЧҹ Ч—Ч•ЧһЧЁЧҷЧқ ЧһЧ•ЧңЧҷЧӣЧҷЧқ. Ч‘ЧӘЧ•Чҡ Ч”ЧһЧ•ЧңЧҷЧӣЧҷЧқ, ЧӘЧ Ч•ЧўЧӘ Ч”ЧҗЧңЧ§ЧҳЧЁЧ•Ч ЧҷЧқ Ч”ЧҷЧҗ Ч§Ч•Ч•ЧҗЧ–Чҷ-Ч—Ч•ЧӨЧ©ЧҷЧӘ Ч•Ч ЧҷЧӘЧ ЧӘ ЧңЧӘЧҷЧҗЧ•ЧЁ Ч‘ЧўЧ–ЧЁЧӘ Ч”ЧҗЧҷЧ‘ЧЁ Ч”Ч§ЧҷЧ ЧҳЧҷ Ч‘Ч”ЧһЧҷЧңЧҳЧ•Ч ЧҷЧҗЧҹ ЧңЧўЧҷЧң ЧўЧқ ЧһЧЎЧ” ЧҗЧӨЧ§ЧҳЧҷЧ‘ЧҷЧӘ m. ЧңЧўЧҷЧӘЧҷЧқ Ч§ЧЁЧ•Ч‘Ч•ЧӘ, ЧӨЧ Чҷ Ч”Ч©ЧҳЧ— Ч©Чң Ч—Ч•ЧһЧЁЧҷЧқ ЧӣЧҗЧңЧ• ЧһЧӣЧ•ЧЎЧҷЧқ Ч‘Ч©ЧӣЧ‘Ч•ЧӘ ЧһЧ—ЧһЧҰЧ Ч•ЧӘ ЧҗЧ• ЧҗЧҷЧ Чқ ЧҗЧҷЧ“ЧҷЧҗЧңЧҷЧҷЧқ ЧһЧЎЧҷЧ‘Ч•ЧӘ ЧҗЧ—ЧЁЧ•ЧӘ. Ч”Ч©ЧӣЧ‘Ч” Ч”Ч“Ч§Ч” Ч•Ч‘ЧңЧӘЧҷ-ЧһЧ•ЧңЧҷЧӣЧ” Ч”Ч–ЧҗЧӘ Ч ЧҷЧӘЧ ЧӘ ЧңЧһЧҷЧ“Ч•Чң ЧўЧң ЧҷЧ“Чҷ ЧӨЧ•ЧҳЧ ЧҰЧҷЧҗЧң Ч“ЧңЧӘЧҗ ЧӣЧһЧ§Ч•Ч“Чқ. ЧҗЧңЧ§ЧҳЧЁЧ•Ч ЧҷЧқ ЧўЧ©Ч•ЧҷЧҷЧқ ЧңЧһЧ Ч”ЧЁ ЧһЧ—Ч•ЧһЧЁ ЧҗЧ—Ч“ ЧңЧҗЧ—ЧЁ, ЧһЧ” Ч©ЧһЧ‘ЧҷЧҗ ЧңЧҷЧҰЧҷЧЁЧӘ Ч–ЧЁЧқ Ч—Ч©ЧһЧңЧҷ Ч‘ЧһЧһЧ©Ч§.
Ч”ЧӨЧўЧ•ЧңЧ” Ч©Чң ЧһЧҷЧ§ЧЁЧ•ЧЎЧ§Ч•ЧӨ ЧһЧ Ч”Ч•ЧЁ ЧЎЧ•ЧЁЧ§ ЧһЧӘЧ‘ЧЎЧЎЧӘ ЧўЧң ЧҗЧӨЧ§Чҳ Ч”ЧһЧ Ч”Ч•ЧЁ Ч”Ч–Ч”. Ч‘ЧһЧ§ЧЁЧ” Ч–Ч”, Ч”ЧһЧ—ЧЎЧ•Чқ Ч”Ч•Чҗ ЧўЧ§Ч‘ Ч”ЧҗЧ•Ч•ЧҷЧЁ Ч‘ЧҷЧҹ Ч§ЧҰЧ” Ч”ЧһЧҷЧ§ЧЁЧ•ЧЎЧ§Ч•ЧӨ Ч•Ч”Ч’Ч•ЧЈ Ч”Ч Ч—Ч§ЧЁ. Ч—Ч•Ч–Ч§ Ч”ЧһЧ—ЧЎЧ•Чқ Ч§Ч©Ч•ЧЁ Ч‘Ч”ЧӨЧЁЧ“Ч” Ч•Ч”Ч•Чҗ Ч—Ч–Ч§ ЧҷЧ•ЧӘЧЁ ЧӣЧӣЧң Ч©Ч”Ч©Ч ЧҷЧҷЧқ ЧЁЧ—Ч•Ч§ЧҷЧқ ЧҷЧ•ЧӘЧЁ. ЧңЧ“ЧҷЧ•Чҹ ЧӣЧңЧңЧҷ ЧҷЧ•ЧӘЧЁ Ч‘ЧЎЧҷЧҳЧ•ЧҗЧҰЧҷЧ” Ч”ЧһЧӘЧ§Ч‘ЧңЧӘ, ЧЁЧҗЧ• Ч’Чқ ЧһЧ—ЧЎЧ•Чқ ЧӨЧ•ЧҳЧ ЧҰЧҷЧҗЧң ЧЎЧ•ЧӨЧҷ.
Ч”ЧһЧ•Ч“Чң ЧңЧўЧҷЧң Ч”Ч•Чҗ Ч—Ч“-ЧһЧһЧ“Чҷ Ч‘ЧўЧ•Ч“ Ч”ЧһЧЁЧ—Ч‘ Ч”ЧЎЧ•Ч‘Ч‘ Ч”Ч•Чҗ ЧӘЧңЧӘ-ЧһЧһЧ“Чҷ, ЧӣЧҡ Ч©ЧңЧһЧўЧ©Ч”, ЧҷЧ© ЧңЧӨЧӘЧ•ЧЁ ЧҗЧӘ ЧһЧ©Ч•Ч•ЧҗЧӘ Ч©ЧЁЧ“ЧҷЧ Ч’ЧЁ Ч‘Ч©ЧңЧ•Ч©Ч” ЧһЧһЧ“ЧҷЧқ. ЧһЧҰЧ“ Ч©Ч Чҷ, ЧһЧўЧЁЧӣЧ•ЧӘ ЧЁЧ‘Ч•ЧӘ ЧһЧ©ЧӘЧ Ч•ЧӘ ЧЁЧ§ ЧңЧҗЧ•ЧЁЧҡ Ч§Ч•ЧҗЧ•ЧЁЧ“ЧҷЧ ЧҳЧ” ЧҗЧ—ЧӘ Ч•ЧҗЧҷЧ Ч•Ч•ЧЁЧҷЧҗЧ ЧҳЧҷЧ•ЧӘ ЧңЧ”Ч–Ч–Ч•ЧӘ Ч‘ЧӣЧҷЧ•Ч•Ч ЧҷЧқ Ч”ЧҗЧ—ЧЁЧҷЧқ. ЧһЧ©Ч•Ч•ЧҗЧӘ Ч©ЧЁЧ“ЧҷЧ Ч’ЧЁ ЧһЧҰЧ•ЧһЧҰЧһЧӘ ЧҗЧ– ЧңЧһЧ§ЧЁЧ” Ч©Ч ЧҷЧ“Ч•Чҹ ЧӣЧҗЧҹ Ч‘ЧҗЧһЧҰЧўЧ•ЧӘ Ч”ЧӨЧЁЧ“ЧӘ ЧһЧ©ЧӘЧ ЧҷЧқ:  .
.
Ч”ЧһЧ•Ч“Чң Ч©Чң ЧӨЧ•ЧҳЧ ЧҰЧҷЧҗЧң Ч“ЧңЧӘЧҗ Ч”Ч•ЧӨЧҡ Ч©ЧҷЧһЧ•Ч©Чҷ Ч‘ЧһЧҷЧ•Ч—Ч“ Ч‘ЧһЧ§ЧЁЧ” Ч©Чң Ч‘Ч•ЧЁ ЧӨЧ•ЧҳЧ ЧҰЧҷЧҗЧң Ч“ЧңЧӘЧҗ ЧӣЧӨЧ•Чң ЧҗЧ©ЧЁ ЧһЧҷЧҷЧҰЧ’ Ч’ЧЁЧЎЧ” Ч—Ч“-ЧһЧһЧ“ЧҷЧӘ Ч©Чң ЧһЧ•ЧңЧ§Ч•ЧңЧӘ ЧһЧҷЧһЧҹ ЧһЧҷЧ•Ч Ч ЧӘ, ЧӣЧӨЧҷ Ч©ЧһЧӘЧ•ЧҗЧЁ Ч‘Ч—ЧңЧ§ Ч”Ч‘Чҗ. Ч‘ЧһЧ§ЧЁЧ” Ч–Ч”, Ч”ЧӨЧ•ЧҳЧ ЧҰЧҷЧҗЧң Ч”Ч—Ч©ЧһЧңЧҷ Ч©Ч—Ч•Ч•Ч” Ч”ЧҗЧңЧ§ЧҳЧЁЧ•Чҹ (Ч”ЧҷЧ—ЧҷЧ“) Ч©Чң ЧһЧ•ЧңЧ§Ч•ЧңЧӘ  Ч”Ч•Чҗ ЧһЧ”ЧҰЧ•ЧЁЧ”:
Ч”Ч•Чҗ ЧһЧ”ЧҰЧ•ЧЁЧ”:  , Ч•ЧңЧӣЧҹ ЧҷЧӣЧ•Чң ЧңЧ”ЧҷЧ•ЧӘ ЧһЧ§Ч•ЧЁЧ‘ Ч‘ЧҰЧ•ЧЁЧ” Ч’ЧЎЧ” ЧўЧң ЧҷЧ“Чҷ Ч–Ч•Ч’ Ч‘Ч•ЧЁЧ•ЧӘ Ч“ЧңЧӘЧҗ. ЧӨЧӘЧЁЧ•Чҹ ЧһЧ©Ч•Ч•ЧҗЧӘ Ч©ЧЁЧ“ЧҷЧ Ч’ЧЁ Ч‘ЧһЧ§ЧЁЧ” Ч–Ч” ЧһЧЁЧҗЧ” Ч©ЧҷЧ©Ч Чқ Ч©Ч Чҷ ЧһЧҰЧ‘ЧҷЧқ Ч§Ч©Ч•ЧЁЧҷЧқ (ЧҗЧ—Ч“ ЧЎЧҷЧһЧҳЧЁЧҷ Ч•Ч”Ч©Ч Чҷ ЧҗЧ ЧҳЧҷ-ЧЎЧҷЧһЧҳЧЁЧҷ) Ч•Ч©Ч”Ч”ЧЎЧӘЧ‘ЧЁЧ•ЧӘ ЧңЧһЧҰЧ•Чҗ ЧҗЧӘ Ч”Ч—ЧңЧ§ЧҷЧ§ Ч‘ЧӣЧң ЧҗЧ—Ч“ ЧһЧ”ЧһЧҰЧ‘ЧҷЧқ Ч©Ч•Ч•Ч”. Ч”ЧӨЧҷЧЁЧ•Ч© Ч”ЧӨЧҷЧ–ЧҷЧ§ЧңЧҷ Ч©Чң Ч”ЧӨЧӘЧЁЧ•Чҹ Ч”Ч•Чҗ Ч©Ч”ЧҗЧңЧ§ЧҳЧЁЧ•Чҹ ЧһЧ‘ЧңЧ” Ч–ЧһЧҹ Ч©Ч•Ч•Ч” Ч‘Ч§ЧЁЧ‘ЧӘ ЧӣЧң ЧӨЧЁЧ•ЧҳЧ•Чҹ, Ч•Ч–Ч”Ч• Ч‘Ч“ЧҷЧ•Ч§ ЧһЧ” Ч©Ч Ч§ЧЁЧҗ Ч‘ЧӣЧҷЧһЧҷЧ” "Ч§Ч©ЧЁ Ч§Ч•Ч•ЧңЧ ЧҳЧҷ ЧҳЧ”Ч•ЧЁ" - Ч‘Ч• Ч©Ч Чҷ ЧҗЧҳЧ•ЧһЧҷЧқ Ч—Ч•ЧңЧ§ЧҷЧқ Ч–Ч•Ч’ ЧҗЧ—Ч“ ЧҗЧ• ЧҷЧ•ЧӘЧЁ Ч©Чң ЧҗЧңЧ§ЧҳЧЁЧ•Ч Чҷ ЧўЧЁЧӣЧҷЧ•ЧӘ, Ч•ЧӨЧ•Ч Ч§ЧҰЧҷЧҷЧӘ Ч”Ч’Чң Ч”ЧһЧӘЧҗЧҷЧһЧ” ЧңЧҗЧ•ЧӘЧқ ЧҗЧңЧ§ЧҳЧЁЧ•Ч ЧҷЧқ ЧҗЧ•ЧӨЧӨЧӘ ЧҗЧӘ Ч©Ч Чҷ Ч”ЧҗЧҳЧ•ЧһЧҷЧқ Ч‘ЧһЧҷЧ“Ч” Ч©Ч•Ч•Ч” (Ч”ЧҰЧӨЧҷЧӨЧ•ЧӘ Ч©Чң ЧўЧ Чҹ Ч”ЧҗЧңЧ§ЧҳЧЁЧ•Ч ЧҷЧқ Ч‘ЧЎЧ‘ЧҷЧ‘ЧӘ ЧӣЧң ЧҗЧ—Ч“ ЧһЧ”ЧҗЧҳЧ•ЧһЧҷЧқ Ч–Ч”Ч”).
, Ч•ЧңЧӣЧҹ ЧҷЧӣЧ•Чң ЧңЧ”ЧҷЧ•ЧӘ ЧһЧ§Ч•ЧЁЧ‘ Ч‘ЧҰЧ•ЧЁЧ” Ч’ЧЎЧ” ЧўЧң ЧҷЧ“Чҷ Ч–Ч•Ч’ Ч‘Ч•ЧЁЧ•ЧӘ Ч“ЧңЧӘЧҗ. ЧӨЧӘЧЁЧ•Чҹ ЧһЧ©Ч•Ч•ЧҗЧӘ Ч©ЧЁЧ“ЧҷЧ Ч’ЧЁ Ч‘ЧһЧ§ЧЁЧ” Ч–Ч” ЧһЧЁЧҗЧ” Ч©ЧҷЧ©Ч Чқ Ч©Ч Чҷ ЧһЧҰЧ‘ЧҷЧқ Ч§Ч©Ч•ЧЁЧҷЧқ (ЧҗЧ—Ч“ ЧЎЧҷЧһЧҳЧЁЧҷ Ч•Ч”Ч©Ч Чҷ ЧҗЧ ЧҳЧҷ-ЧЎЧҷЧһЧҳЧЁЧҷ) Ч•Ч©Ч”Ч”ЧЎЧӘЧ‘ЧЁЧ•ЧӘ ЧңЧһЧҰЧ•Чҗ ЧҗЧӘ Ч”Ч—ЧңЧ§ЧҷЧ§ Ч‘ЧӣЧң ЧҗЧ—Ч“ ЧһЧ”ЧһЧҰЧ‘ЧҷЧқ Ч©Ч•Ч•Ч”. Ч”ЧӨЧҷЧЁЧ•Ч© Ч”ЧӨЧҷЧ–ЧҷЧ§ЧңЧҷ Ч©Чң Ч”ЧӨЧӘЧЁЧ•Чҹ Ч”Ч•Чҗ Ч©Ч”ЧҗЧңЧ§ЧҳЧЁЧ•Чҹ ЧһЧ‘ЧңЧ” Ч–ЧһЧҹ Ч©Ч•Ч•Ч” Ч‘Ч§ЧЁЧ‘ЧӘ ЧӣЧң ЧӨЧЁЧ•ЧҳЧ•Чҹ, Ч•Ч–Ч”Ч• Ч‘Ч“ЧҷЧ•Ч§ ЧһЧ” Ч©Ч Ч§ЧЁЧҗ Ч‘ЧӣЧҷЧһЧҷЧ” "Ч§Ч©ЧЁ Ч§Ч•Ч•ЧңЧ ЧҳЧҷ ЧҳЧ”Ч•ЧЁ" - Ч‘Ч• Ч©Ч Чҷ ЧҗЧҳЧ•ЧһЧҷЧқ Ч—Ч•ЧңЧ§ЧҷЧқ Ч–Ч•Ч’ ЧҗЧ—Ч“ ЧҗЧ• ЧҷЧ•ЧӘЧЁ Ч©Чң ЧҗЧңЧ§ЧҳЧЁЧ•Ч Чҷ ЧўЧЁЧӣЧҷЧ•ЧӘ, Ч•ЧӨЧ•Ч Ч§ЧҰЧҷЧҷЧӘ Ч”Ч’Чң Ч”ЧһЧӘЧҗЧҷЧһЧ” ЧңЧҗЧ•ЧӘЧқ ЧҗЧңЧ§ЧҳЧЁЧ•Ч ЧҷЧқ ЧҗЧ•ЧӨЧӨЧӘ ЧҗЧӘ Ч©Ч Чҷ Ч”ЧҗЧҳЧ•ЧһЧҷЧқ Ч‘ЧһЧҷЧ“Ч” Ч©Ч•Ч•Ч” (Ч”ЧҰЧӨЧҷЧӨЧ•ЧӘ Ч©Чң ЧўЧ Чҹ Ч”ЧҗЧңЧ§ЧҳЧЁЧ•Ч ЧҷЧқ Ч‘ЧЎЧ‘ЧҷЧ‘ЧӘ ЧӣЧң ЧҗЧ—Ч“ ЧһЧ”ЧҗЧҳЧ•ЧһЧҷЧқ Ч–Ч”Ч”).
ЧӨЧ•ЧҳЧ ЧҰЧҷЧҗЧң Ч“ЧңЧӘЧҗ ЧӣЧӨЧ•Чң
 ЧӨЧ•Ч Ч§ЧҰЧҷЧ•ЧӘ Ч”Ч’Чң Ч”ЧЎЧҷЧһЧҳЧЁЧҷЧ•ЧӘ Ч•Ч”ЧҗЧ ЧҳЧҷ-ЧЎЧҷЧһЧҳЧЁЧҷЧ•ЧӘ Ч‘ЧўЧ‘Ч•ЧЁ Ч‘Ч•ЧЁ ЧӨЧ•ЧҳЧ ЧҰЧҷЧҗЧң Ч“ЧңЧӘЧҗ ЧӣЧӨЧ•Чң ЧўЧқ "ЧһЧЁЧ—Ч§ Ч‘ЧҷЧҹ Ч’ЧЁЧўЧҷЧ Чҷ" R=2.
ЧӨЧ•Ч Ч§ЧҰЧҷЧ•ЧӘ Ч”Ч’Чң Ч”ЧЎЧҷЧһЧҳЧЁЧҷЧ•ЧӘ Ч•Ч”ЧҗЧ ЧҳЧҷ-ЧЎЧҷЧһЧҳЧЁЧҷЧ•ЧӘ Ч‘ЧўЧ‘Ч•ЧЁ Ч‘Ч•ЧЁ ЧӨЧ•ЧҳЧ ЧҰЧҷЧҗЧң Ч“ЧңЧӘЧҗ ЧӣЧӨЧ•Чң ЧўЧқ "ЧһЧЁЧ—Ч§ Ч‘ЧҷЧҹ Ч’ЧЁЧўЧҷЧ Чҷ" R=2.
Ч‘Ч•ЧЁ Ч”Ч“ЧңЧӘЧҗ Ч”ЧӣЧӨЧ•Чң ЧһЧһЧ“Чң ЧһЧ•ЧңЧ§Ч•ЧңЧӘ ЧһЧҷЧһЧҹ Ч“Ч•-ЧҗЧҳЧ•ЧһЧҷЧӘ Ч‘ЧўЧ–ЧЁЧӘ ЧһЧ©Ч•Ч•ЧҗЧӘ Ч©ЧЁЧ“ЧҷЧ Ч’ЧЁ Ч”ЧһЧӘЧҗЧҷЧһЧ”:

ЧӣЧҗЧ©ЧЁ Ч”ЧӨЧ•ЧҳЧ ЧҰЧҷЧҗЧң ЧӣЧўЧӘ Ч”Ч•Чҗ:
![{\displaystyle V(x)=-q\lambda \left[\delta \left(x+{\frac {R}{2}}\right)+\delta \left(x-{\frac {R}{2}}\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dcee2f68b39e89b655e2100d8eaced7bf113a885)
ЧӣЧҗЧ©ЧЁ  Ч”Ч•Чҗ Ч”ЧһЧЁЧ—Ч§ Ч”Ч‘ЧҷЧҹ Ч’ЧЁЧўЧҷЧ Чҷ Ч•Ч”ЧӨЧ•ЧҳЧ ЧҰЧҷЧҗЧң Ч”Ч•Чҗ ЧңЧһЧўЧ©Ч” ЧӨЧ•Ч Ч§ЧҰЧҷЧҷЧӘ Ч“ЧңЧӘЧҗ Ч©Чң Ч“ЧҷЧЁЧҗЧ§ ЧўЧқ Ч©Ч Чҷ Ч©ЧҷЧҗЧҷЧқ Ч©ЧңЧҷЧңЧҷЧҷЧқ Ч”ЧһЧһЧ•Ч§ЧһЧҷЧқ Ч‘-x =ВұR/2 (ЧһЧ•ЧЁЧҗЧҷЧқ Ч‘Ч—Ч•Чқ Ч‘Ч“ЧҷЧҗЧ’ЧЁЧһЧ”). Ч ЧўЧ‘Ч•Ч“ Ч‘ЧҷЧ—ЧҷЧ“Ч•ЧӘ ЧҗЧҳЧ•ЧһЧҷЧ•ЧӘ Ч•Ч ЧҰЧҷЧ‘
Ч”Ч•Чҗ Ч”ЧһЧЁЧ—Ч§ Ч”Ч‘ЧҷЧҹ Ч’ЧЁЧўЧҷЧ Чҷ Ч•Ч”ЧӨЧ•ЧҳЧ ЧҰЧҷЧҗЧң Ч”Ч•Чҗ ЧңЧһЧўЧ©Ч” ЧӨЧ•Ч Ч§ЧҰЧҷЧҷЧӘ Ч“ЧңЧӘЧҗ Ч©Чң Ч“ЧҷЧЁЧҗЧ§ ЧўЧқ Ч©Ч Чҷ Ч©ЧҷЧҗЧҷЧқ Ч©ЧңЧҷЧңЧҷЧҷЧқ Ч”ЧһЧһЧ•Ч§ЧһЧҷЧқ Ч‘-x =ВұR/2 (ЧһЧ•ЧЁЧҗЧҷЧқ Ч‘Ч—Ч•Чқ Ч‘Ч“ЧҷЧҗЧ’ЧЁЧһЧ”). Ч ЧўЧ‘Ч•Ч“ Ч‘ЧҷЧ—ЧҷЧ“Ч•ЧӘ ЧҗЧҳЧ•ЧһЧҷЧ•ЧӘ Ч•Ч ЧҰЧҷЧ‘  . ЧӣЧҗЧҹ
. ЧӣЧҗЧҹ  Ч”Ч•Чҗ ЧӨЧЁЧһЧҳЧЁ ЧӨЧ•ЧЁЧһЧңЧҷ Ч ЧҷЧӘЧҹ ЧңЧ©ЧҷЧ Ч•Чҷ. ЧһЧ”ЧӨЧӘЧЁЧ•Чҹ ЧңЧ‘Ч•ЧЁ ЧӨЧ•ЧҳЧ ЧҰЧҷЧҗЧң Ч“ЧңЧӘЧҗ ЧҷЧ—ЧҷЧ“, Ч Ч•ЧӣЧң ЧңЧ‘ЧҰЧў "Ч ЧҷЧ—Ч•Ч© ЧһЧ•Ч©ЧӣЧң" Ч•ЧңЧ”ЧЎЧҷЧ§ Ч©Ч”ЧӨЧӘЧЁЧ•Чҹ Ч”Ч•Чҗ ЧһЧ”ЧҰЧ•ЧЁЧ”:
Ч”Ч•Чҗ ЧӨЧЁЧһЧҳЧЁ ЧӨЧ•ЧЁЧһЧңЧҷ Ч ЧҷЧӘЧҹ ЧңЧ©ЧҷЧ Ч•Чҷ. ЧһЧ”ЧӨЧӘЧЁЧ•Чҹ ЧңЧ‘Ч•ЧЁ ЧӨЧ•ЧҳЧ ЧҰЧҷЧҗЧң Ч“ЧңЧӘЧҗ ЧҷЧ—ЧҷЧ“, Ч Ч•ЧӣЧң ЧңЧ‘ЧҰЧў "Ч ЧҷЧ—Ч•Ч© ЧһЧ•Ч©ЧӣЧң" Ч•ЧңЧ”ЧЎЧҷЧ§ Ч©Ч”ЧӨЧӘЧЁЧ•Чҹ Ч”Ч•Чҗ ЧһЧ”ЧҰЧ•ЧЁЧ”:

ЧһЧӘЧӨЧҷЧЁЧӘ Ч—ЧңЧ§Чҷ ЧӨЧ•Ч Ч§ЧҰЧҷЧҷЧӘ Ч”Ч’Чң Ч‘Ч©ЧҷЧҗЧҷ Ч”Ч“ЧңЧӘЧҗ Ч Ч§Ч‘Чң ЧҗЧӘ Ч”Ч“ЧҳЧЁЧһЧҷЧ Ч ЧҳЧ”:

ЧңЧӨЧҷЧӣЧҡ,  Ч Ч©ЧңЧҳ ЧўЧң ЧҷЧ“Чҷ Ч”ЧһЧ©Ч•Ч•ЧҗЧ” "Ч”ЧӨЧЎЧҗЧ•Ч“Ч•-ЧЁЧҷЧ‘Ч•ЧўЧҷЧӘ":
Ч Ч©ЧңЧҳ ЧўЧң ЧҷЧ“Чҷ Ч”ЧһЧ©Ч•Ч•ЧҗЧ” "Ч”ЧӨЧЎЧҗЧ•Ч“Ч•-ЧЁЧҷЧ‘Ч•ЧўЧҷЧӘ":
![{\displaystyle d_{\pm }(\lambda )~=~{\textstyle {\frac {1}{2}}}q(\lambda +1)\pm {\textstyle {\frac {1}{2}}}\left\{q^{2}(1+\lambda )^{2}-4\,\lambda q^{2}\lbrack 1-e^{-2d_{\pm }(\lambda )R}]\right\}^{1/2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/02509c77fbbd368bfbb4680bfed7062d06a7eedc)
ЧҗЧ©ЧЁ ЧңЧ” ЧҷЧ© Ч©Ч Чҷ ЧӨЧӘЧЁЧ•Ч Ч•ЧӘ  . Ч‘ЧўЧ‘Ч•ЧЁ Ч”ЧһЧ§ЧЁЧ” Ч©Чң ЧһЧҳЧўЧ ЧҷЧқ Ч©Ч•Ч•ЧҷЧқ (Ч©Ч Чҷ Ч’ЧЁЧўЧҷЧ ЧҷЧқ Ч–Ч”ЧҷЧқ), О» = 1 Ч•Ч”ЧһЧ©Ч•Ч•ЧҗЧ” Ч”ЧӨЧЎЧҗЧ•Ч“Ч•-ЧЁЧҷЧ‘Ч•ЧўЧҷЧӘ ЧһЧҰЧ•ЧһЧҰЧһЧӘ Чң-:
. Ч‘ЧўЧ‘Ч•ЧЁ Ч”ЧһЧ§ЧЁЧ” Ч©Чң ЧһЧҳЧўЧ ЧҷЧқ Ч©Ч•Ч•ЧҷЧқ (Ч©Ч Чҷ Ч’ЧЁЧўЧҷЧ ЧҷЧқ Ч–Ч”ЧҷЧқ), О» = 1 Ч•Ч”ЧһЧ©Ч•Ч•ЧҗЧ” Ч”ЧӨЧЎЧҗЧ•Ч“Ч•-ЧЁЧҷЧ‘Ч•ЧўЧҷЧӘ ЧһЧҰЧ•ЧһЧҰЧһЧӘ Чң-:
![{\displaystyle d_{\pm }=q[1\pm e^{-d_{\pm }R}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/de3c25340e952fe2d73d65c9047a1eab7295c663)
ЧһЧ§ЧЁЧ” Ч”-"+" ЧһЧӘЧҗЧҷЧқ ЧңЧӨЧ•Ч Ч§ЧҰЧҷЧҷЧӘ Ч’Чң ЧЎЧҷЧһЧҳЧЁЧҷЧӘ ЧЎЧ‘ЧҷЧ‘ Ч Ч§Ч•Ч“ЧӘ Ч”ЧҗЧһЧҰЧў (ЧӨЧӘЧЁЧ•Чҹ Ч–Ч” ЧһЧ•ЧЁЧҗЧ” Ч‘ЧҗЧ“Ч•Чқ Ч‘ЧҗЧҷЧ•ЧЁ ЧңЧўЧҷЧң). Ч‘Ч”ЧӘЧҗЧһЧ”, ЧһЧ§ЧЁЧ” Ч”-"-" ЧһЧҷЧҷЧҰЧ’ ЧӨЧ•Ч Ч§ЧҰЧҷЧҷЧӘ Ч’Чң ЧҗЧ ЧҳЧҷ-ЧЎЧҷЧһЧҳЧЁЧҷЧӘ ЧһЧЎЧ‘ЧҷЧ‘ ЧңЧ Ч§Ч•Ч“ЧӘ Ч”ЧҗЧһЧҰЧў (ЧһЧ•ЧЁЧҗЧ” Ч‘ЧҷЧЁЧ•Ч§ Ч‘ЧҗЧҷЧ•ЧЁ). Ч”Чқ ЧһЧҷЧҷЧҰЧ’ЧҷЧқ Ч§ЧҷЧЁЧ•Ч‘ Ч©Чң Ч©ЧӘЧҷ ЧЁЧһЧ•ЧӘ Ч”ЧҗЧ ЧЁЧ’ЧҷЧ” Ч”Ч ЧһЧ•ЧӣЧ•ЧӘ Ч‘ЧҷЧ•ЧӘЧЁ Ч©Чң ЧһЧ•ЧңЧ§Ч•ЧңЧӘ  ЧӘЧңЧӘ-ЧһЧһЧ“ЧҷЧӘ Ч•Ч”Чқ Ч©ЧҷЧһЧ•Ч©ЧҷЧҷЧқ Ч‘ЧҗЧ ЧңЧҷЧ–Ч” Ч©ЧңЧ”. ЧӨЧӘЧЁЧ•Ч Ч•ЧӘ ЧҗЧ ЧңЧҷЧҳЧҷЧҷЧқ ЧңЧўЧЁЧӣЧҷЧқ Ч”ЧўЧҰЧһЧҷЧҷЧқ Ч©Чң Ч”ЧҗЧ ЧЁЧ’ЧҷЧ” Ч‘ЧһЧ§ЧЁЧ” Ч©Чң ЧһЧҳЧўЧ ЧҷЧқ ЧЎЧҷЧһЧҳЧЁЧҷЧҷЧқ Ч ЧҷЧӘЧҹ ЧўЧң ЧҷЧ“Чҷ:
ЧӘЧңЧӘ-ЧһЧһЧ“ЧҷЧӘ Ч•Ч”Чқ Ч©ЧҷЧһЧ•Ч©ЧҷЧҷЧқ Ч‘ЧҗЧ ЧңЧҷЧ–Ч” Ч©ЧңЧ”. ЧӨЧӘЧЁЧ•Ч Ч•ЧӘ ЧҗЧ ЧңЧҷЧҳЧҷЧҷЧқ ЧңЧўЧЁЧӣЧҷЧқ Ч”ЧўЧҰЧһЧҷЧҷЧқ Ч©Чң Ч”ЧҗЧ ЧЁЧ’ЧҷЧ” Ч‘ЧһЧ§ЧЁЧ” Ч©Чң ЧһЧҳЧўЧ ЧҷЧқ ЧЎЧҷЧһЧҳЧЁЧҷЧҷЧқ Ч ЧҷЧӘЧҹ ЧўЧң ЧҷЧ“Чҷ:

ЧӣЧҗЧ©ЧЁ W Ч”ЧҷЧҗ ЧӨЧ•Ч Ч§ЧҰЧҷЧҷЧӘ W Ч©Чң ЧңЧһЧ‘ЧЁЧҳ. Ч©ЧҷЧһЧ• ЧңЧ‘ Ч©Ч”ЧҗЧ ЧЁЧ’ЧҷЧ” Ч”Ч ЧһЧ•ЧӣЧ” Ч‘ЧҷЧ•ЧӘЧЁ ЧһЧӘЧҗЧҷЧһЧ” ЧңЧӨЧӘЧЁЧ•Чҹ Ч”ЧЎЧҷЧһЧҳЧЁЧҷ  . Ч‘ЧһЧ§ЧЁЧ” Ч©Чң ЧһЧҳЧўЧ ЧҷЧқ ЧңЧҗ Ч©Ч•Ч•ЧҷЧқ Ч•ЧһЧ•Ч“Чң ЧһЧ•ЧңЧ§Ч•ЧңЧЁЧҷ ЧӘЧңЧӘ-ЧһЧһЧ“Чҷ, Ч”ЧӨЧӘЧЁЧ•Ч Ч•ЧӘ Ч ЧҷЧӘЧ ЧҷЧқ ЧўЧң ЧҷЧ“Чҷ Ч”ЧӣЧңЧңЧ” Ч©Чң ЧӨЧ•Ч Ч§ЧҰЧҷЧҷЧӘ W Ч©Чң ЧңЧһЧ‘ЧЁЧҳ.
. Ч‘ЧһЧ§ЧЁЧ” Ч©Чң ЧһЧҳЧўЧ ЧҷЧқ ЧңЧҗ Ч©Ч•Ч•ЧҷЧқ Ч•ЧһЧ•Ч“Чң ЧһЧ•ЧңЧ§Ч•ЧңЧЁЧҷ ЧӘЧңЧӘ-ЧһЧһЧ“Чҷ, Ч”ЧӨЧӘЧЁЧ•Ч Ч•ЧӘ Ч ЧҷЧӘЧ ЧҷЧқ ЧўЧң ЧҷЧ“Чҷ Ч”ЧӣЧңЧңЧ” Ч©Чң ЧӨЧ•Ч Ч§ЧҰЧҷЧҷЧӘ W Ч©Чң ЧңЧһЧ‘ЧЁЧҳ.
ЧЁЧҗЧ• Ч’Чқ
Ч§ЧҷЧ©Ч•ЧЁЧҷЧқ Ч—ЧҷЧҰЧ•Ч ЧҷЧҷЧқ