בור פוטנציאל סופי
|
Read other articles:

Jordens Peters Informasi pribadiNama lengkap Jordens PetersTanggal lahir 3 Mei 1987 (umur 36)Tempat lahir Nijmegen, BelandaTinggi 1,82 m (5 ft 11+1⁄2 in)Posisi bermain BekInformasi klubKlub saat ini Willem IINomor 4Karier junior BMC FC Den BoschKarier senior*Tahun Tim Tampil (Gol)2005–2012 FC Den Bosch 180 (3)2012– Willem II 12 (1) * Penampilan dan gol di klub senior hanya dihitung dari liga domestik dan akurat per 14:17, 2 September 2012 (UTC) Jordens Pete...

Penyuntingan Artikel oleh pengguna baru atau anonim untuk saat ini tidak diizinkan.Lihat kebijakan pelindungan dan log pelindungan untuk informasi selengkapnya. Jika Anda tidak dapat menyunting Artikel ini dan Anda ingin melakukannya, Anda dapat memohon permintaan penyuntingan, diskusikan perubahan yang ingin dilakukan di halaman pembicaraan, memohon untuk melepaskan pelindungan, masuk, atau buatlah sebuah akun. Suku TorajaTo Raya, To Raa, To RiajaAnak perempuan Toraja pada upacara pernikahan...

1989 Garfield TV special Garfield's ThanksgivingThe TitleCreated byJim DavisWritten byJim DavisKim CampbellDirected byPhil RomanCo-directorsGerard BaldwinBob NeslerJohn SpareyStarringLorenzo MusicThom HugeGregg BergerJulie PaynePat CarrollTheme music composerEd Bogas and Desirée Goyette (music and lyrics)Lou Rawls and Desirée Goyette (vocals)Country of originUnited StatesOriginal languageEnglishProductionProducerPhil RomanRunning time24 minutesProduction companiesFilm RomanUnited MediaPaws,...

Hermann de WiedFonctionsArchevêque de CologneArchidiocèse de Cologne1515-1547Philip II of Daun-Oberstein (en)Adolphe XIII de SchaumbourgPrince-électeurÉlectorat de Cologne1515-1547Administrateur diocésainDiocèse de Paderborn (d)BiographieNaissance 14 janvier 1477Château fort de AltwiedDécès 15 août 1552 (à 75 ans)Activité Prêtre catholiquePère Frédéric de Wied (d)Mère Agnès de Virnebourg (d)modifier - modifier le code - modifier Wikidata Hermann de Wied (allem...

كأس أوروبا 1958–59أقيم النهائي على مرسيدس بنز أرينا في شتوتغارت.تفاصيل المسابقةالتواريخ26 أغسطس 1958 – 3 يونيو 1959الفرق28المراكز النهائيةالبطل ريال مدريدالوصيف ستاد ريمسإحصائيات المسابقةالمباريات الملعوبة55الأهداف المسجلة199 (3٫62 لكل مباراة)أفضل هداف جاست فونتين (10 أهداف)�...
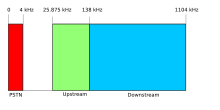
تحتاج النصوص المترجمة في هذه المقالة إلى مراجعة لضمان معلوماتها وإسنادها وأسلوبها ومصطلحاتها ووضوحها للقارئ، لأنها تشمل ترجمة اقتراضية أو غير سليمة. فضلاً ساهم في تطوير هذه المقالة بمراجعة النصوص وإعادة صياغتها بما يتناسب مع دليل الأسلوب في ويكيبيديا. (سبتمبر 2019) ترددات �...

Jayachamarajendra Wadiyar BahadurGCB, GCSI Maharaja MysoreBerkuasa1940–1950Penobatan29 Agustus 1940, Istana MysorePendahuluKrishnaraja Wadiyar IVPenerusSrikanta WadiyarKelahiran(1919-07-18)18 Juli 1919Istana Mysore, Mysore, Kerajaan Mysore, IndiaKematian23 September 1974(1974-09-23) (umur 55)Istana Bangalore, Bangalore, IndiaWangsaDinasti WadiyarAyahYuwaraja Kanteerawa Narasimharaja WadiyarIbuYuwarani Kempu Cheluwaja AmanniAnakPutri Gayatri Dewi Awaru, Putri Meenakshi Dewi Awaru, Putri...

この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。出典を追加して記事の信頼性向上にご協力ください。(このテンプレートの使い方)出典検索?: コルク – ニュース · 書籍 · スカラー · CiNii · J-STAGE · NDL · dlib.jp · ジャパンサーチ · TWL(2017年4月) コルクを打ち抜いて作った瓶の栓 コルク(木栓、�...

Dylan Dogserie regolare a fumetti Logo della serie Lingua orig.italiano PaeseItalia TestiTiziano Sclavi, Roberto Recchioni, Luigi Mignacco, Claudio Chiaverotti, Gianfranco Manfredi, Michele Medda, Pasquale Ruju, Giuseppe De Nardo, Paola Barbato, Tito Faraci, Michele Masiero, Alessandro Bilotta, Andrea Cavaletto, Carlo Ambrosini, Fabio Celoni, Giovanni Di Gregorio, Bruno Enna, Giovanni Gualdoni, Mauro Marcheselli, Giancarlo Marzano, Robin Wood, Fabrizio Accatino, Barbara Baraldi, Gig...

Olympic gymnastics event Men's vaultat the Games of the XXII OlympiadNikolai Andrianov (c. 1974)VenueLuzhniki Palace of SportsDate20–25 JulyCompetitors65 from 14 nationsWinning score19.825Medalists Nikolai Andrianov Soviet Union Alexander Dityatin Soviet Union Roland Brückner East Germany← 19761984 → Gymnastics at the1980 Summer OlympicsList of gymnastsArtisticTeam all-aroundmenwomenIndividual all-aroundmenwomenVaultmenwomenFloormenwomenPommel...

French online dating service MeeticCompany typeSubsidiaryIndustryOnline dating serviceFounded2001HeadquartersBoulogne-Billancourt, FranceKey peopleMarc Simoncini, CEORevenue€133.6 M (Europe, 2008)[needs update]ParentMatch GroupWebsitewww.meetic.com Meetic is a French online dating service founded in November 2001.[1] It is recognized for its intuitive interface and matching algorithms that suggest potential partners to users based on profile attributes.[2] Meetic bec...

此条目序言章节没有充分总结全文内容要点。 (2019年3月21日)请考虑扩充序言,清晰概述条目所有重點。请在条目的讨论页讨论此问题。 哈萨克斯坦總統哈薩克總統旗現任Қасым-Жомарт Кемелұлы Тоқаев卡瑟姆若马尔特·托卡耶夫自2019年3月20日在任任期7年首任努尔苏丹·纳扎尔巴耶夫设立1990年4月24日(哈薩克蘇維埃社會主義共和國總統) 哈萨克斯坦 哈萨克斯坦政府...

Este artículo o sección necesita referencias que aparezcan en una publicación acreditada. Busca fuentes: «Avenida Blanco Encalada» – noticias · libros · académico · imágenesEste aviso fue puesto el 16 de marzo de 2015. Avenida Blanco Encalada SantiagoSantiago, Chile Chile Datos de la rutaNumeración 1600 al 3100Ancho de calzada 5 pistas por sentido (entre plaza Ercilla y calle San Alfonso)3 pistas por sentido (San Alfonso y avenida Exposición)Lo...

Marie IKing of SedangRaja SedangBerkuasa3 Juni 1888 - 11 November 1890PenerusJules Georges Piquetsebagai Gubernur-Jenderal Indochina PrancisInformasi pribadiKelahiran(1842-01-31)31 Januari 1842Toulon, PrancisKematian11 November 1890(1890-11-11) (umur 48)Pulau Tioman, Malaya Britania Marie-Charles David de Mayréna (juga dikenal sebagai Charles-Marie David de Mayréna dan Marie I, Raja Sedang; 31 Januari 1842 – 11 November 1890) adalah seorang petualang eksentrik asal Pran...

Australian television channel Television channel Sky News ExtraCountryAustraliaBroadcast areaAustraliaProgrammingLanguage(s)EnglishPicture format576i (SDTV 16:9)1080i (HDTV)OwnershipOwnerFoxtelSister channelsSky News AustraliaSky News Weather ChannelHistoryLaunched20 January 2009; 15 years ago (2009-01-20)ReplacedSky News Election ChannelReplaced bySky News Election Channel (linear channel; 1 May 2016 – 23 January 2017)Former namesA-PACAvailabilityTerrestrialFoxtel603Strea...

Португальская Республикапорт. República Portuguesa Флаг Герб Гимн: «A Portuguesa» Расположение Португалии (тёмно-зелёный):— в Европе (светло-зелёный и тёмно-серый)— в Европейском союзе (светло-зелёный) Основано 26 июля 1139 года Дата независимости 1 декабря 1640 года как Королевство Португа...
علم صربيا والجبل الأسود التسمية علم صربيا والجبل الأسود (بالصربية: Застава Србије и Црне Горе) التناسب 1:2 ألوان أزرق أبيض أحمر الاعتماد 27 أبريل 1992 (إزالة النجمة الحمراء من علم يوغوسلافيا) الاختصاص صربيا والجبل الأسود التصميم ثلاثة أشرطة أفقية من ألوان الأزرق والأبيض...

Men's freestyle 130 kgat the Games of the XXVII OlympiadVenueSydney Convention and Exhibition CentreDate29 September – 1 October 2000Competitors18 from 18 nationsMedalists David Musulbes Russia Artur Taymazov Uzbekistan Alexis Rodríguez Cuba← 19962004 → Wrestling at the2000 Summer OlympicsQualificationFreestyleGreco-Roman54 kg54 kg58 kg58 kg63 kg63 kg69 kg69 kg76 kg76 kg85 kg85 kg97 kg97 kg130 kg130 kgvte Main article: Wrestling at the 2000...

For other groups with similar names, see Sisters of Charity and Daughters of Charity (disambiguation). Society of apostolic life Daughters of Charity of Saint Vincent de PaulSaint Louise de Marillac, Co-founder of the Company of the Daughters of Charity of Saint Vincent de PaulAbbreviationD.C.Established29 November 1633; 390 years ago (29 November 1633)FoundersSt. Vincent de PaulSt. Louise de MarillacFounded atParis, FranceTypeCentralized Religious Institute of Consecrated Life o...

Some of this article's listed sources may not be reliable. Please help improve this article by looking for better, more reliable sources. Unreliable citations may be challenged and removed. (July 2021) (Learn how and when to remove this message) French concession of HankowConcession française de Hankou漢口法租界Foreign concession of Second French Republic, Second French Empire, French Third Republic and French State1896–1943 FlagHistory • Established 1896• Disestabl...





























































































![{\displaystyle ka=n\pi -\sin ^{-1}\left[k\hbar /{\sqrt {2mV_{1}}}\right]-\sin ^{-1}\left[k\hbar /{\sqrt {2mV_{2}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f08fecd77dd909fa45cd3fabbb29bdd139c6e0e2)
