אקספוננט
|
Read other articles:

This article is about the sampling technique used in biological studies. For the structural reliability analysis method, see Line Sampling. Click to see animation of line-intercept sampling. In statistics, more specifically in biostatistics, line-intercept sampling (LIS) is a method of sampling elements in a region whereby an element is sampled if a chosen line segment, called a “transect”, intersects the element.[1] Line intercept sampling has proven to be a reliable, versatile, ...

Phobos 2Penggambaran wahana PhobosOperatorIKITipe misiPengorbitSatelit dariMarsTanggal memasuki orbit29 Januari 1989Tanggal perluncuran12 Juli 1988Wahana peluncurRoket Proton-KID COSPAR1988-059ASitus webMisi PhobosBerat2600 kg (6220 kg dengan perangkat keras insersi orbit) Program Phobos (Rusia: Фобос, Foboscode: ru is deprecated , Greek: Φόβοςcode: el is deprecated ) adalah misi tak berawak yang terdiri dari dua wahana yang diluncurkan oleh Uni Soviet untuk mempelajari Mars dan sat...
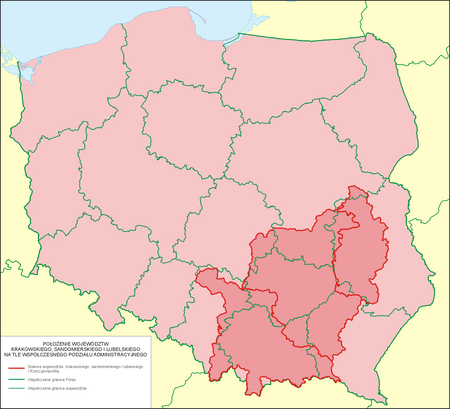
Историческая областьМалая Польшапольск. Małopolska Герб Медиафайлы на Викискладе Малая Польша (польск. Małopolska, Mało-Polska) — историческая область на юго-востоке и юге современной Польши. Её столицей и крупнейшим городом является Краков. На протяжении веков на территории М�...

Artikel ini membutuhkan rujukan tambahan agar kualitasnya dapat dipastikan. Mohon bantu kami mengembangkan artikel ini dengan cara menambahkan rujukan ke sumber tepercaya. Pernyataan tak bersumber bisa saja dipertentangkan dan dihapus.Cari sumber: Virgin Gorda – berita · surat kabar · buku · cendekiawan · JSTOR (June 2018) Virgin GordaMenghadap North Sound, 2010Virgin GordaLokasi Virgin Gorda di Kepulauan Virgin InggrisTampilkan peta Kepulauan Virgin I...

This article is about a series of seacoast guns. For the contemporary field gun, see 3-inch M1902 field gun. Rapid-fire seacoast gun 3-inch gun M1898, M1902, M1903 3-inch gun M1903TypeRapid-fire seacoast gunPlace of originUnited StatesService historyIn service1899–1945Used byUnited States Army Coast Artillery CorpsWarsWorld War I and World War IIProduction historyDesigned M1898: 1898 M1902: 1902 M1903: 1903 Manufacturer M1898: Driggs-Seabury M1902: Bethlehem Steel M1903:...

Questa voce o sezione sull'argomento autorità unitarie dell'Inghilterra non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Derbyautorità unitaria e cittàCity of Derby Derby – Veduta LocalizzazioneStato Regno Unito Inghilterra RegioneMidlands Orientali Contea Derbyshire AmministrazioneEsecutivoLaburista / Conservatore Ter...

Australian bushranger Martin CashBorn1808 (1808)Enniscorthy, County Wexford, IrelandDied26 August 1877 (1877-08-27)Glenorchy, Tasmania, AustraliaSpouseMary Bennett (1824–1879)ChildrenMartin Cash (1855–1871)[1] Martin Cash (baptised 10 October 1808 – 26 August 1877) was a notorious Irish-Australian convict bushranger, known for escaping twice from Port Arthur, Van Diemen's Land. His 1870 autobiography, The Adventures of Martin Cash, ghostwritten by James Lester Burke, a...

Pour les articles homonymes, voir Éducation (homonymie) et Éducateur. Ne doit pas être confondu avec Enseignement. Moyen mnémotechnique mis à disposition des enfants visitant le Field Museum de Chicago leur permettant d'apprendre les pays formant l'Asie et leurs contours géographiques. L’éducation est l'apprentissage et le développement des facultés intellectuelles, morales et physiques, les moyens et les résultats de cette activité de développement. L'éducation inclut des com...

Francia Uniformi di gara Prima tenuta Tenuta alternativa Sport Rugby a 15 Federazione Fédération Française de Rugby Soprannome «Les Bleues» C.T. Thomas Darracq Record presenze Laëtitia Salles (92) Piazzamento 4ª (2 maggio 2022) Sponsor tecnico Le Coq sportif Esordio internazionale Paesi Bassi 0-4 FranciaUtrecht, 13 giugno 1982 Migliore vittoria Francia 99-0 GiapponeEdimburgo, 17 aprile 1994 Peggiore sconfitta Francia 0-109 Nuova ZelandaEdmonton, 14 settembre 1996 Coppa del Mondo Parte...

Yumi, Yumi, YumiLagu kebangsaan VanuatuPenulis lirikFrançois Vincent AyssavKomponisFrançois Vincent AyssavPenggunaan1980Sampel audioYumi, Yumi, Yumi (instrumental)berkasbantuan Sampel audioYumi, Yumi, Yumiberkasbantuan Yumi, Yumi, Yumi (bahasa Bislama: Kami, Kami, Kami) adalah lagu kebangsaan dari Vanuatu. Lagu ini ditulis dan disusun oleh François Vincent Ayssav (lahir 1955) dan diadopsi pada tahun 1980. Bahasa Bislama Refrain: Yumi, yumi, yumi i glat blong talem se Yumi, yumi, yumi...

This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (January 2013) (Learn how and when to remove this message) You can help expand this article with text translated from the corresponding article in Serbian. (May 2024) Click [show] for important translation instructions. Machine translation, like DeepL or Google Translate, is a useful starting point for trans...

National highway in India. Previously it was NH 102. National Highway 722Map of National Highway 722 in redRoute informationLength74 km (46 mi)Major junctionsFromMuzaffarpurToChhapra LocationCountryIndiaStatesBiharPrimarydestinationsRewaghat Highway system Roads in India Expressways National State Asian ← NH 22→ NH 31 National Highway 722 (NH 722) is a National Highway in India. This highway runs entirely in the state of Bihar.[1] References ^ Rationalisation of Num...

Basaluzzo komune di Italia Basaluzzo (it) Tempat Negara berdaulatItaliaDaerah di ItaliaPiemonteProvinsi di ItaliaProvinsi Alessandria NegaraItalia Ibu kotaBasaluzzo PendudukTotal2.007 (2023 )GeografiLuas wilayah15,05 km² [convert: unit tak dikenal]Ketinggian149 m Berbatasan denganCapriata d'Orba Francavilla Bisio Novi Ligure Predosa Bosco Marengo Fresonara Pasturana SejarahHari liburpatronal festival Santo pelindungYoakhim Informasi tambahanKode pos15060 Zona waktuUTC+1 UTC+2 Kode...

Division of Poland into powiats (counties) Contour map of Poland indicating modern voivodeshipsAdministrativedivisions of Poland VoivodeshipsPowiats (list)Gminas (list) vte The following is an alphabetical list of all 380 county-level entities in Poland. A county or powiat (pronounced povyat, /pɔv.jät/) is the second level of Polish administrative division, between the voivodeship (provinces) and the gmina (municipalities or communes; plural gminy). The list includes the 314 land counties ...

This article includes a list of references, related reading, or external links, but its sources remain unclear because it lacks inline citations. Please help improve this article by introducing more precise citations. (May 2020) (Learn how and when to remove this message) The Truth-Teller's Tale First editionAuthorSharon ShinnCover artistMatt MahurinCountryUnited StatesLanguageEnglishSeriesSafe-Keepers SeriesGenreFantasyPublisherViking JuvenilePublication date2005Media typePrint (Ha...

Town in Syria Town in Rif Dimashq, SyriaMaaloula ܡܥܠܘܠܐمعلولاTownOverview of Maaloula, 2006MaaloulaLocation in SyriaCoordinates: 33°50′39″N 36°32′48″E / 33.84417°N 36.54667°E / 33.84417; 36.54667Country SyriaGovernorateRif DimashqDistrictal-QutayfahSubdistrictMaaloulaElevation1,500 m (4,900 ft)Population (2004 census)[1] • Total2,762 Maaloula (Arabic: مَعلُولَا; Western Neo-Aramaic: ܡܥܠܘܠܐ ,...

اقتُرح دمج محتويات هذه المقالة مع المعلومات الموجودة في طفل أنابيب. (ناقش) إخصاب في المختبر مخطط لتلقيح صناعي خارج الجسم بواسطة الحقن المجهري. معلومات عامة من أنواع تخصيب، وتقنيات التلقيح بالمساعدة تعديل مصدري - تعديل الإخْصَاب في المُخْتَبَر[1][2] ويسمى ح...

ميغيل لوبيز دي ليغازبي ميغيل لوبيز دي ليجازبي ، في المجلة الإسبانية لا هورميجا دي أورو. معلومات شخصية اسم الولادة ميغل لوبيز دي ليغازبي[1] الميلاد 1502ثوماراغا، غيبوثكوا، تاج قشتالة، إسبانيا الوفاة 20 أغسطس 1572 (عمر 69–70)انتراموروس، الفلبين سبب الوفاة سكتة دماغية مكان ا...

2022年紐約州聯邦參議員選舉 ← 2016 2022年11月8日 2028 → 获提名人 查克·舒默 喬·皮尼恩 政党 民主党 共和黨 政党联盟 工作家庭黨 保守黨 民選得票 3320561 2501151 得票率 56.8% 42.8% 縣結果 眾議院選區結果舒默: 40–50% 50–60% 60–70% 70–80% 80–90% 皮尼恩: ...

此條目需要补充更多来源。 (2024年3月9日)请协助補充多方面可靠来源以改善这篇条目,无法查证的内容可能會因為异议提出而被移除。致使用者:请搜索一下条目的标题(来源搜索:几何原本 — 网页、新闻、书籍、学术、图像),以检查网络上是否存在该主题的更多可靠来源(判定指引)。 《中國圖說》中的插图:利玛窦和徐光启[1] 摘抄自徐光啟手書《刻〈幾何�...


























































