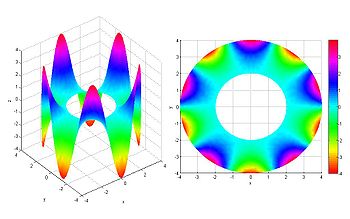
Ecuación diferencial
|
Read other articles:

Motif in art and culture For use in biology (phylogeny), see Tree of life (biology). For other uses, see Tree of life (disambiguation). An 1847 depiction of the Norse Yggdrasil as described in the Icelandic Prose Edda by Oluf Olufsen Bagge 17th-century depiction of the tree of life in Palace of Shaki Khans, Azerbaijan Confronted animals, here ibexes, flank a tree of life, a very common motif in the art of the ancient Near East and Mediterranean Breastfeeding before an Egyptian sycamore The tr...

Kaisarea Maritima beralih ke halaman ini. Untuk kegunaan lain, lihat Kaisarea (disambiguasi). Kaisarea קֵיסָרְיָהTranskripsi Ibrani • standarKeisarya • resmiQesaryaKaisarea MaritimaDistrikHaifaLuas35.000 dunams (35 km2 or 14 sq mi)Populasi (2006)4.400 • Kepadatan0,13/km2 (0,33/sq mi) Kaisarea (atau Kaisaria; Ibrani: קֵיסָרְיָה, qaisariyah; Arab: قيساريةcode: ar is deprecated , Qaysaria;...

Untuk versi televisi 2015, lihat The Dresser (film 2015). The DresserSutradaraPeter YatesProduserPeter YatesDitulis olehRonald HarwoodPemeran Albert Finney Tom Courtenay Edward Fox Zena Walker Eileen Atkins Michael Gough Cathryn Harrison Penata musikJames HornerSinematograferKelvin PikePenyuntingRay LovejoyDistributorColumbia PicturesTanggal rilis 9 Desember 1983 (1983-12-09) Durasi118 menitNegaraBritania RayaBahasaInggrisPendapatankotor$5,310,748 The Dresser adalah sebuah film 198...

Historic building in Salt Lake City, Utah, U.S. United States historic placeThomas Kearns Mansion and Carriage HouseU.S. National Register of Historic Places Governor's Mansion, March 2010Show map of UtahShow map of the United StatesLocation603 East South Temple StreetSalt Lake City, UtahUnited StatesCoordinates40°46′11″N 111°52′23″W / 40.76972°N 111.87306°W / 40.76972; -111.87306Area9 acres (3.6 ha)Built1900-02ArchitectNeuhausen, Carl M.NRHP refe...

Modern tradition of Wicca This article does not cite any sources. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Faery Wicca – news · newspapers · books · scholar · JSTOR (July 2023) (Learn how and when to remove this template message) Faery WiccaAbbreviationFWPart of a series onWiccaPentacle History of Wicca History of Wicca Etymology of Wicca Bricket Wood coven ...

Village in Lancashire, England Human settlement in EnglandCoupe GreenThe Old Oak Inn public house, Coupe GreenCoupe GreenShown within South RibbleShow map of the Borough of South RibbleCoupe GreenLocation within LancashireShow map of LancashireOS grid referenceSD592275DistrictSouth RibbleShire countyLancashireRegionNorth WestCountryEnglandSovereign stateUnited KingdomPost townPRESTONPostcode districtPR5Dialling code01254PoliceLancashireFireLancashireAmbulanceNort...

Mitsubishi 1MF9 atau Mitsubishi Experimental Taka-type Carrier Fighter adalah prototipe pesawat tempur Jepang tahun 1920-an. Biplane satu kursi tunggal bermesin dimaksudkan untuk beroperasi dari kapal induk Angkatan Laut Kekaisaran Jepang, tetapi hanya dua yang dibangun, dengan tipe yang sedang ditolak oleh Angkatan Laut. Referensi Wikimedia Commons memiliki media mengenai Mitsubishi military aircraft. Mikesh, Robert C and Shorzoe Abe. Japanese Aircraft 1910–1941. London:Putnam, 1990. ISBN...

Metre-based systems of measurement For a topical guide, see Outline of the metric system. A kilogram mass and three metric measuring devices: a tape measure in centimetres, a thermometer in degrees Celsius, and a multimeter that measures potential in volts, current in amperes and resistance in ohms. The metric system is a decimal-based system of measurement. The current international standard for the metric system is the International System of Units (Système international d'unités or SI), ...

Public university in Hamilton, Ontario McMaster UniversityArms of McMaster UniversityLatin: Universitas MacmastrensisMottoΤὰ πάντα ἐν Χριστῷ συνέστηκεν (Greek)Motto in EnglishIn Christ all things consist[1]TypePublic universityEstablished23 April 1887(137 years ago) (1887-04-23)[note 1][4]AffiliationACUCARLCOUFields InstituteIAUUniversities CanadaU15U21EndowmentCA$908.7 million[5]ChancellorSantee SmithPresidentDav...

1993 single by Common SenseSoul by the PoundSingle by Common Sensefrom the album Can I Borrow a Dollar? B-sideCan-I-Bust, Heidi HoeReleasedJuly 13, 1993GenreHip hopLength4:20LabelRelativity RecordsSongwriter(s)Common, No I.D., Anthony CraigProducer(s)Immenslope, The Twilite ToneCommon Sense singles chronology Breaker 1/9 (1993) Soul by the Pound (1993) I Used to Love H.E.R. (1994) Soul by the Pound is the third single from rapper Common Sense's 1992 debut album, Can I Borrow a Dollar?. It...
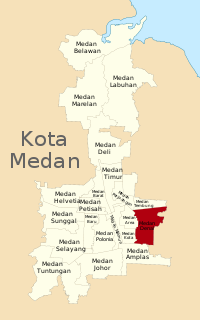
Medan DenaiKecamatanPeta lokasi Kecamatan Medan DenaiMedan DenaiPeta lokasi Kecamatan Medan DenaiKoordinat: 3°34′32″N 98°43′30″E / 3.575501°N 98.725103°E / 3.575501; 98.725103Koordinat: 3°34′32″N 98°43′30″E / 3.575501°N 98.725103°E / 3.575501; 98.725103Negara IndonesiaProvinsiSumatera UtaraKotaMedanPemerintahan • CamatBaharuddin Ritonga[1]Populasi (2021)[2] • Total169.643 ...

فيلاهيرموسا (بالإسبانية: Villahermosa) تاريخ التأسيس 24 يونيو 1564 تقسيم إداري البلد المكسيك [1][2] عاصمة لـ تاباسكو خصائص جغرافية إحداثيات 17°59′16″N 92°55′10″W / 17.9878375°N 92.919416111111°W / 17.9878375; -92.919416111111 المساحة 80 كيلومتر مربع الارتفاع 11 متر ا...

هذه المقالة بحاجة لصندوق معلومات. فضلًا ساعد في تحسين هذه المقالة بإضافة صندوق معلومات مخصص إليها. يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (ديسمبر 2018) قرن: ق�...

Chinese jelly made of mung bean starch For the southern Chinese dessert, see grass jelly. LiangfenSichuan-style liangfenTraditional Chinese涼粉Simplified Chinese凉粉Hanyu Pinyinliángfěn Literal meaningcool powderTranscriptionsStandard MandarinHanyu PinyinliángfěnYue: CantoneseJyutpingloeng4 fen2 Liangfen (simplified Chinese: 凉粉; traditional Chinese: 涼粉; pinyin: liángfěn; lit. 'cool powder'), also spelled liang fen, is a Chinese legume dish consisting...

العلاقات التنزانية السيشلية تنزانيا سيشل تنزانيا سيشل تعديل مصدري - تعديل العلاقات التنزانية السيشلية هي العلاقات الثنائية التي تجمع بين تنزانيا وسيشل.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية للدولتين: وجه المقارنة تنزا�...

Geometric figure The unit hyperbola is blue, its conjugate is green, and the asymptotes are red. In geometry, the unit hyperbola is the set of points (x,y) in the Cartesian plane that satisfy the implicit equation x 2 − y 2 = 1. {\displaystyle x^{2}-y^{2}=1.} In the study of indefinite orthogonal groups, the unit hyperbola forms the basis for an alternative radial length r = x 2 − y 2 . {\displaystyle r={\sqrt {x^{2}-y^{2}}}.} Whereas the unit circle surrounds its center, the un...

Dalam nama yang mengikuti kebiasaan penamaan Slavia Timur ini, patronimiknya adalah Dmitriyevich dan nama keluarganya adalah Protasevich. Roman ProtasevichNama asalРоман Протасевич Раман ПратасевічLahirRoman Dmitryevich Protasevich5 Mei 1995 (umur 29)[1]Minsk,[butuh rujukan] BelarusPendidikanUniversitas Negeri BelarusPekerjaanWartawanaktivisfotograferTahun aktif2011–saat iniOrganisasiNextaGerakan politikFront PemudaPasanganSof...

ValstagnamunicipioValstagna – VedutaValstagna ed il fiume Brenta LocalizzazioneStato Italia Regione Veneto Provincia Vicenza ComuneValbrenta TerritorioCoordinate45°51′42″N 11°39′32″E45°51′42″N, 11°39′32″E (Valstagna) Altitudine157 m s.l.m. Abitanti1 816[1] (31-12-2015) SottodivisioniCollicello, Costa, Oliero, San Gaetano, Sasso Stefani Altre informazioniCod. postale36029 (già 36020) Prefisso0424 Fuso orarioUTC+1 Cod. catastaleL...

Extinct breed of scent hound This article is about the extinct breed of stag hunting scent hound. For other uses, see Staghound (disambiguation). Dog breedStaghoundOther namesEnglish StaghoundOriginEnglandBreed statusExtinctTraitsHeight Up to 27 in (69 cm)Coat ShortColour Usually bi-colour; white with yellow, lemon or badgerDog (domestic dog) The Staghound, sometimes referred to as the English Staghound, is an extinct breed of scent hound from England. A pack hound, the breed was us...

Three meals eaten by Shabbat-observant Jews on Shabbat Part of a series onJudaism Movements Orthodox Haredi Hasidic Modern Conservative Conservadox Reform Karaite Reconstructionist Renewal Humanistic Haymanot Philosophy Principles of faith Kabbalah Messiah Ethics Chosenness God Names Musar movement Texts Tanakh Torah Nevi'im Ketuvim Ḥumash Siddur Piyutim Zohar Rabbinic Mishnah Talmud Midrash Tosefta Law Mishneh Torah Tur Shulchan Aruch Mishnah Berurah Aruch HaShulchan Kashrut Tz...