Équation de Riccati
|
Read other articles:

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Januari 2023. Koordinat: 39°11′58″N 127°08′16″E / 39.199469°N 127.137823°E / 39.199469; 127.137823 Air terjun Ullim pada 2008 Air terjun Ullim [nb 1] ( 울림 폭포 ) adalah sebuah air terjun yang terletak di luar Wŏnsan...

Katedral SucreGereja Katedral Metropolitan Bunda GuadalupeKatedral SucreLokasiSucreNegaraBoliviaDenominasiGereja Katolik RomaSejarahDedikasiBunda dari GuadalupeArsitekturStatusKatedralStatus fungsionalAktifAdministrasiKeuskupan AgungKeuskupan Agung Sucre Katedral Metropolitan Sucre, juga disebut Basilika Katedral Bunda Maria dari Guadalupe adalah sebuah gereja katedral Katolik yang terletak di kota Sucre, Bolivia, yang sekaligus menjadi pusat Gereja Katolik di Bolivia. Dibangun antara tahun 1...

Dutch fashion photographer duo A major contributor to this article appears to have a close connection with its subject. It may require cleanup to comply with Wikipedia's content policies, particularly neutral point of view. Please discuss further on the talk page. (April 2023) (Learn how and when to remove this template message) Vinoodh Matadin and Inez van Lamsweerde in June 2011 Inez van Lamsweerde (born 25 September 1963) and Vinoodh Matadin (born 29 September 1961) are a Dutch-American fa...

Stadion Letjen H. Soedirman Bojonegoro Informasi stadionNama lengkapStadion Letjen H. Soedirman BojonegoroPemilikPemkot BojonegoroLokasiLokasiJalan Lisman, Karang Pacar-Campurjo Bojonegoro, Jawa Timur, Indonesia[1]Koordinat7°8′53″S 111°54′2″E / 7.14806°S 111.90056°E / -7.14806; 111.90056[2]KonstruksiDibuat1980Dibuka1983Direnovasi2010Data teknisPermukaanRumputKapasitas20.000[3][4]PemakaiPersibo Bojonegoro[5]Sunting kot...

L'Institut pour la protection du patrimoine de la ville de Belgrade L'architecture de Belgrade présente des constructions très variées, du quartier de Zemun, qui, longtemps sous domination autrichienne, offre l'aspect typique d'une ville d'Europe centrale, jusqu'à l'architecture la plus moderniste, telle qu'on peut la trouver à Novi Beograd. Si la forteresse de Belgrade abrite les édifices les plus anciens de la capitale, en raison des nombreuses destructions que la ville a connues, les...

Arnaldo Ruggero IVConte di Pallars SobiràStemma In carica1424 - 1451 PredecessoreRuggero Bernardo I SuccessoreUgo Ruggero III Nome completoArnaldo Ruggero Altri titoliViceré di Sicilia e conestabile della corona d'Aragona Nascita1400 circa Morte1451 circa PadreRuggero Bernardo I MadreBeatrice di Cardona ConsorteGiovanna di Cardona FigliMargheritaUgo Ruggero eGiovanna ReligioneCattolicesimo Arnaldo Ruggero IV di Pallars Sobirà (in spagnolo Arnal Rogelio, in catalano Arnau Ro...

American baseball player Baseball player Mickey TettletonCatcherBorn: (1960-09-16) September 16, 1960 (age 63)Oklahoma City, Oklahoma, U.S.Batted: SwitchThrew: RightMLB debutJune 30, 1984, for the Oakland AthleticsLast MLB appearanceJuly 2, 1997, for the Texas RangersMLB statisticsBatting average.241Home runs245Runs batted in732 Teams Oakland Athletics (1984–1987) Baltimore Orioles (1988–1990) Detroit Tigers (1991–1994) Texas Rangers (1995–1997) Care...

52.50713.372027777778Koordinaten: 52° 30′ 25,2″ N, 13° 22′ 19,3″ O Das Theater während der Berlinale 2017 Das Theater am Potsdamer Platz ist ein Musicaltheater im Berliner Ortsteil Tiergarten. Geschichte Frontansicht des Theaters am Potsdamer Platz Foyer des Theaters am Potsdamer Platz Der Theaterbau des Architekten Renzo Piano am Marlene-Dietrich-Platz wurde am 2. Oktober 1998 in der Nähe des Potsdamer Platzes fertiggestellt und eröffnete am 5. Juni...

1938-1965 American comic strip This article is about the comic strip. For other uses, see Red Ryder (disambiguation). Red RyderA page from Dell Comics' Red Ryder #25 (May–June 1945) reprinting 1943 comic strips by Fred HarmanAuthor(s)Stephen Slesinger and Fred HarmanCurrent status/scheduleEndedLaunch dateNovember 6, 1938End dateSeptember 30, 1965Syndicate(s)Newspaper Enterprise AssociationGenre(s)Western This article needs additional citations for verification. Please help improve this arti...

Australian politician (1926–2014) The HonourableNeville WranAC, CNZM, QCWran c. 1971Chairman of the CSIROIn office5 December 1986 – 4 December 1991Preceded byNorman BoardmanSucceeded byAdrienne Clarke35th Premier of New South WalesElections: 1976, 1978, 1981, 1984In office14 May 1976 – 4 July 1986MonarchElizabeth IIGovernorSir Roden Cutler (1976–81)Sir James Rowland (1981–86)DeputyJack Ferguson (1976–84)Ron Mulock (1984–86)Preceded bySir Eric Wi...

此條目可参照英語維基百科相應條目来扩充。 (2021年5月6日)若您熟悉来源语言和主题,请协助参考外语维基百科扩充条目。请勿直接提交机械翻译,也不要翻译不可靠、低品质内容。依版权协议,译文需在编辑摘要注明来源,或于讨论页顶部标记{{Translated page}}标签。 约翰斯顿环礁Kalama Atoll 美國本土外小島嶼 Johnston Atoll 旗幟颂歌:《星條旗》The Star-Spangled Banner約翰斯頓環礁�...

Сельское поселение России (МО 2-го уровня)Новотитаровское сельское поселение Флаг[d] Герб 45°14′09″ с. ш. 38°58′16″ в. д.HGЯO Страна Россия Субъект РФ Краснодарский край Район Динской Включает 4 населённых пункта Адм. центр Новотитаровская Глава сельского пос�...

Pour les articles homonymes, voir Devos. Raymond DevosRaymond Devos en 1980.BiographieNaissance 9 novembre 1922Mouscron (Hainaut, Belgique)Décès 15 juin 2006 (à 83 ans)Saint-Rémy-lès-Chevreuse (Yvelines, France)Sépulture Saint-Rémy-lès-ChevreuseNom de naissance Raymond Pierre DevosNationalité françaiseActivités Humoriste, artiste de cirque, artiste de cabaret, acteurPériode d'activité 1948-2005Conjoint Simone Beguin (d) (de 1959 à 1999)Autres informationsLabels Philips Rec...

This is a list of trolleybus systems in Ukraine by oblast. It includes all trolleybus systems, past and present. LAZ trolleybus in Ternopil, Ukraine Cherkasy Oblast Location Date (from) Date (to) Notes Cherkasy 9 November 1965 Chernihiv Oblast Location Date (from) Date (to) Notes Chernihiv 4 November 1964 Chernivtsi Oblast Location Date (from) Date (to) Notes Chernivtsi 1 February 1939 Autonomous Republic of Crimea Location Date (from) Date (to) Notes Alushta 20 August 1993 See also Simferop...
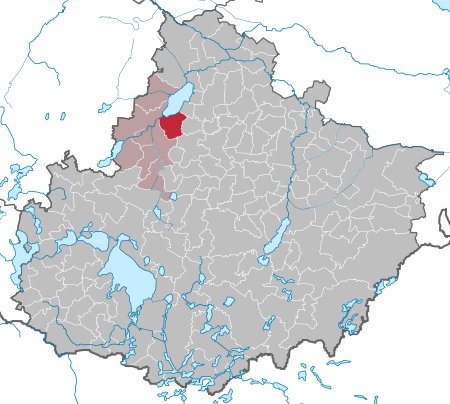
For Kummerow near Stralsund, see Kummerow, Nordvorpommern. Municipality in Mecklenburg-Vorpommern, GermanyKummerow MunicipalityKummerow am See - Baroque castle Coat of armsLocation of Kummerow within Mecklenburgische Seenplatte district Kummerow Show map of GermanyKummerow Show map of Mecklenburg-VorpommernCoordinates: 53°46′N 12°50′E / 53.767°N 12.833°E / 53.767; 12.833CountryGermanyStateMecklenburg-VorpommernDistrictMecklenburgische Seenplatte Municipal assoc...

Инкассаторский автомобиль с охраной в городе Гуанчжоу Нали́чные де́ньги, нали́чность, в противоположность безналичным деньгам — валюта одной из стран в каком-либо физическом представлении (обычно купюры; реже монеты) у конкретного физического или юридического лица ...

UFC mixed martial arts event in 2020 UFC on ESPN: Hermansson vs. VettoriThe poster for UFC on ESPN: Hermansson vs. VettoriInformationPromotionUltimate Fighting ChampionshipDateDecember 5, 2020 (2020-12-05)VenueUFC ApexCityEnterprise, Nevada, United StatesAttendanceNone (behind closed doors)[1]Event chronology UFC on ESPN: Smith vs. Clark UFC on ESPN: Hermansson vs. Vettori UFC 256: Figueiredo vs. Moreno UFC on ESPN: Hermansson vs. Vettori (also known as UFC on ESPN 19 a...

Cet article est une ébauche concernant le Nord-Pas-de-Calais, le catholicisme et l’histoire. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Diocèse de Saint-Omer(la) Dioecesis Audomarensis La cathédrale Notre-Dame de Saint-Omer Informations générales Type de juridiction diocèse Création 1559 Suppression 1790 / 1801 Province ecclésiastique Cambrai Siège Saint-Omer Localisation du diocèse (en) Notice ...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Scouting in Kentucky – news · newspapers · books · scholar · JSTOR (February 2017) (Learn how and when to remove this message) Daniel C. Beard Boyhood Home Scouting in Kentucky has a long history, from the 1910s to the present day, serving thousands of youth i...

American clergyman, writer and activist George D. HerronHerron, c. 1900Appointed United States Delegue to the Conference on the Princes' Islands[1]In officeFebruary 1919 – February 1919 Personal detailsBornGeorge Davis Herron(1862-01-21)January 21, 1862Montezuma, Indiana, United StatesDiedNovember 9, 1925(1925-11-09) (aged 63)Munich, GermanyPolitical partySocialist Labor Party of AmericaSocial Democratic Party of AmericaSocialist Party of AmericaSpouse(s)Mary V. Everha...

































