Tore maximal

En mathématiques, un tore maximal d'un groupe de Lie G est un sous-groupe de Lie commutatif, connexe et compact de G qui soit maximal pour ces propriétés. Les tores maximaux de G sont uniques à conjugaison près. De manière équivalente, c'est un sous-groupe de Lie (en) de G, isomorphe à un tore, et maximal pour cette propriété. Le quotient du normalisateur N(T) d'un tore T par T est le groupe de Weyl associé.

Définition

Tout groupe de Lie commutatif connexe est isomorphe à un quotient de Rn par un sous-réseau, donc à un tore Tn. La commutativité et la connexité impliquent en effet que l'exponentielle gG est un morphisme surjectif de groupes de Lie, dont le noyau est un sous-groupe additif discret de g.

Un tore maximal d'un groupe de Lie G est par définition un sous-groupe fermé commutatif et connexe maximal, ou encore un sous-groupe de Lie isomorphe à un tore Tn.

Les sous-groupes de Lie connexes de G sont exactement déterminés par les sous-algèbres de Lie de g. Dans cette correspondance biunivoque, les sous-groupes connexes et commutatifs correspondent aux sous-algèbres commutatives de g. En particulier, dans un groupe de Lie, tout sous-groupe compact commutatif connexe est inclus dans un tore maximal.

Les considérations sur les tores maximaux ont leur importance en particulier dans l'étude des représentations d'un groupe de Lie. En effet, il est facile d'obtenir la classification des représentations d'un tore.

Groupes de Lie compact

Article détaillé : Groupe de Lie compact.

Dans un groupe de Lie compact, l'application exponentielle est surjective. En particulier, tout élément de G appartient à l'image d'un sous-groupe à un paramètre de G. L'adhérence de cette image est un sous-groupe fermé commutatif de G, donc inclus dans un tore maximal de G. De fait :

  • Tout élément d'un groupe de Lie compact appartient à un tore maximal.

Propriétés

Tous les tores maximaux de G sont conjugués et en particulier ont même dimension k, appelée le rang du groupe de Lie G.

Si un élément g commute avec tous les éléments d'un tore maximal T de G, le centralisateur C de g est un sous-groupe de Lie de G, contenant par choix de g le tore T. Il est clair que T est un tore maximal de C. L'élément g de C appartient à un tore maximal de C, donc est conjugué dans C à un élément de T. Comme g est dans le centre de C, g appartient à T. D'où le résultat.

  • L'intersection des tores maximaux de G est exactement le centre de G.

Comme tout élément de G appartient à au moins un tore maximal, le centre de G est égal à l'intersection des centralisateurs des tores maximaux de G. Or, le centralisateur d'un tore maximal est lui-même ; le résultat en découle.

Groupe de Weyl

Article détaillé : Groupe de Weyl.

Le normalisateur de T (dans G) est un sous-groupe fermé de G, et de ce fait, par le théorème de Cartan un sous-groupe de Lie de G. Le groupe de Weyl W(T) associé à T est le quotient du normalisateur de T dans G par T. Il s'avère que T est la composante neutre (en) de son normalisateur. De manière équivalente, W(T) est un groupe fini.

Groupe de Lie semi-simples

Article détaillé : Algèbre de Lie semi-simple.

Le rang d'un groupe de Lie semi-simple est égal au nombre de sommets du diagramme de Dynkin associé.

Read other articles:

I Am Me.

I Am Me.Album mini karya Weki MekiDirilis18 November 2021 (2021-11-18)GenreK-popHip hopR&BDurasi20:04Label Fantagio Kakao M Kronologi Weki Meki New Rules(2020) I Am Me.(2021) Singel dalam album I Am Me. SiestaDirilis: 18 November 2021 I Am Me. adalah album mini kelima dari girl grup Korea Selatan Weki Meki. Ini dirilis pada 18 November 2021, oleh Fantagio dan didistribusikan oleh Kakao Entertainment Ini terdiri dari enam lagu, termasuk lagu utama Siesta. Pra-rilis Album ini diumu...

 

County di Rumania

Peta county di Rumania dan Munisipalitas Bukares Rumania Artikel ini adalah bagian dari seri Politik dan KetatanegaraanRumania Undang-Undang Dasar Referendum 1991 (pengesahan) 2003 (amendemen) 2015 (amendemen) Mahkamah Konstitusi Pemerintah Presiden (daftar) Klaus Iohannis Perdana Menteri (daftar) Nicolae Ciucă Kabinet (saat ini, daftar) Parlemen Senat Presiden: Florin Cîțu Biro Tetap Dewan Perwakilan Presiden: Marcel Ciolacu Biro Tetap Yudikatif Pengadilan Tinggi Kasasi dan Keadilan Mahka...

 

Aonyx

Aonyx[1] Aonyx cinerea Klasifikasi ilmiah Kerajaan: Animalia Filum: Chordata Kelas: Mamalia Ordo: Carnivora Famili: Mustelidae Subfamili: Lutrinae Genus: AonyxLesson, 1827 Spesies tipe Aonyx delalandiLesson, 1827 Species Aonyx capensis Aonyx cinerea Daerah penyebaran Aonyx adalah genus dari hewan berang-berang yang terdiri dari tiga spesies yaitu berang-berang nircakar afrika, berang-berang nircakar kamerun serta sero ambrang. Sero ambrang (Amblonyx cinerea) terkadang juga dimasukkan...

1732 en France

Chronologies 22 janvier : mariage du Prince de Conti et de Mademoiselle de Chartres à la Chapelle de Versailles.Données clés 1729 1730 1731  1732  1733 1734 1735Décennies :1700 1710 1720  1730  1740 1750 1760Siècles :XVIe XVIIe  XVIIIe  XIXe XXeMillénaires :-Ier Ier  IIe  IIIe Chronologies thématiques Art Architecture, Arts plastiques (Dessin, Gravure, Peinture et Sculpture), Littérature, Musique classique et Théâtre  ...

 

Richard Blackburn

Australian judge This article is about the Australian judge. For the Church of England bishop, see Richard Blackburn (bishop). For the colonial Virginia architect, see Rippon Lodge. The Hon.Sir Richard BlackburnOBEA photograph of Sir Richard BlackburnPersonal detailsBorn(1918-07-26)26 July 1918Mount Lofty, South AustraliaDied1 October 1987(1987-10-01) (aged 69)SpouseBryony Helen BlackburnChildrenCharlotte CalderTom BlackburnParent(s)Arthur Seaforth BlackburnRose Ada (née) KellyEducation...

 

Constitutional Union (Morocco)

Political party in Morocco Constitutional Union الاتحاد الدستوري ⴰⵍⵉⵜⵜⵉⴰⴷ ⴰⴷⴷⵓⵔⵜⵓⵔⵉ Union ConstitutionelleLeaderMohammed SajidFounderMaati BouabidFounded10 April 1983; 41 years ago (1983-04-10)HeadquartersRabat, MoroccoIdeologyMonarchism[1][2]Liberal conservatism[3]Conservative liberalism[4][5]Economic liberalism[6]Populism[7]Political positionCentre-right[1]...

Aaron Laffey

American baseball player (born 1985) Baseball player Aaron LaffeyLaffey with the Toronto Blue JaysPitcherBorn: (1985-04-15) April 15, 1985 (age 38)Cumberland, Maryland, U.S.Batted: LeftThrew: LeftMLB debutAugust 4, 2007, for the Cleveland IndiansLast MLB appearanceJuly 31, 2015, for the Colorado RockiesMLB statisticsWin–loss record26–29Earned run average4.44Strikeouts245 Teams Cleveland Indians (2007–2010) Seattle Mariners (2011) New York Yankees (2011...

 

Синелобый амазон

Синелобый амазон Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:ЗавропсидыКласс:Пт�...

 

Teori relativitas

Bagian dari seri artikel mengenaiRelativitas umum G μ ν + Λ g μ ν = 8 π G c 4 T μ ν {\displaystyle G_{\mu \nu }+\Lambda g_{\mu \nu }={8\pi G \over c^{4}}T_{\mu \nu }} PengantarSejarah Rumus matematis SumberUji coba Prinsip dasar Teori relativitas Kerangka acuan Kerangka acuan inersia Prinsip ekuivalensi Ekuivalensi massa–energi Relativitas khusus Garis dunia Geometri Riemann Fenomena Masalah Kepler Gravitasi Medan gravitasi Lensa gravi...

Treviso Foot-Ball Club 1993 2006-2007

Voce principale: Treviso Foot-Ball Club 1993. Treviso Foot-Ball ClubStagione 2006-2007Sport calcio Squadra Treviso Allenatore Diego Bortoluzzi (1ª-10ª) Ezio Rossi (11ª-42ª) Presidente Ettore Setten Serie B12º posto Coppa ItaliaPrimo turno Maggiori presenzeCampionato: Avramov (38)Totale: Avramov (38) Miglior marcatoreCampionato: Acquafresca (11) StadioStadio Omobono Tenni Abbonati1 769[1] Maggior numero di spettatori9 748 vs.  Juventus (16 ottobre 2006) Minor ...

 

Akira Yoshino

Akira YoshinoNama asal吉野 彰Lahir30 Januari 1948 (umur 76)Suita, JepangPendidikanUniversitas Kyoto (BS, MS)Universitas Osaka (PhD)PenghargaanIEEE Medal for Environmental and Safety Technologies (2012)Global Energy Prize (2013)Charles Stark Draper Prize (2014)Japan Prize (2018)Penghargaan Nobel Kimia (2019)Karier ilmiahBidangElektrokimiaInstitusiAsahi KaseiUniversitas Meijo Akira Yoshino (吉野 彰code: ja is deprecated , Yoshino Akira, lahir 30 Januari 1948) adalah kimiawan Je...

 

Tariff of 1792

Historical United States tariff Tariff of 17922nd United States Congress Long title An Act supplementary to the act making provision for the Debt of the United States. CitationPub. L.Tooltip Public Law (United States) 2–381 Stat. 281, Chap. 38Enacted by2nd United States CongressEnactedMay 8, 1792Signed byGeorge WashingtonSummaryU.S. Congressional bill was the fourth public debt resolution. Act provided to extend the term allowed for receiving, on loans, that part of...

قصر شبرا (الطائف)

21°17′10.89″N 40°24′54.15″E / 21.2863583°N 40.4150417°E / 21.2863583; 40.4150417   ميّز عن قصر شبرا.قصر شبراالجهة الأمامية لقصر شبرامعلومات عامةنوع المبنى قصر تاريخيالمكان الطائف، منطقة مكة المكرمةالمنطقة الإدارية محافظة الطائف البلد  السعودية الطائف، منطقة مكة المكرمةمعلومات أ...

 

قائمة أهداف فرناندو توريس الدولية

توريس حاملاً الحذاء الذهبي في كأس القارات 2013. فرناندو توريس هو لاعب كرة قدم إسباني دولي مثل بلاده 110 مرَّات وسجل 38 هدفاً منذ بدايته في عام 2003 ونهايته في 2014. اعتبارًا من فبراير 2017، أصبح توريس ثالث أكبر هدَّاف في تاريخ المنتخب الوطني، حيث سجل دافيد فيا (59 هدفاً) وراؤول غونزاليس ...

 

كلية طب الأسنان (الجامعة الأردنية)

  لمعانٍ أخرى، طالع كلية طب الأسنان (توضيح). كلية طب الأسنان شعار كلية طب الأسنان (الجامعة الأردنية)شعار الكلية مبنى كلية طب الأسنان من الجهة الشرقية. الشعار تطوير الرعاية الصحية السنية من خلال تدريب أطباء أسنان متميزين، وإجراء بحوث علمية ذات جودة عالية.[1] معلومات �...

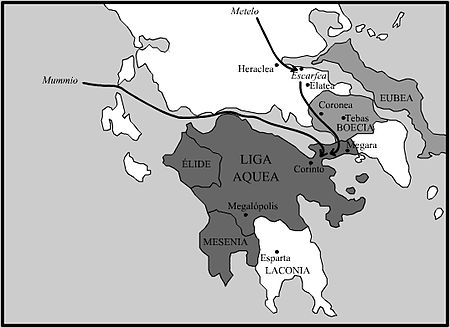
Achaean War

War in 146 BC between Rome and the Achaean League Achaean WarPart of the Macedonian warsThe last day of Corinth, Tony Robert-Fleury, 1870Date146 BCLocationMainland GreeceResult Roman victoryTerritorialchanges Roman annexation of mainland GreeceBelligerents Roman Republic Achaean LeagueCommanders and leaders Metellus MacedonicusLucius Mummius Achaicus CritolaosDiaeus vteAchaean War Scarpheia Corinth (146 BC) The Achaean War of 146 BC was fought between the Roman Republic and the Greek Achaean ...

 

Kementerian Perminyakan dan Sumber Daya Mineral Mesir

Kementerian Perminyakan dan Sumber Daya Mineral Mesir Situs webhttp://www.petroleum.gov.eg/ Kementerian Perminyakan dan Sumber Daya Mineral Mesir (bahasa Arab: وزارة البترول والثروة المعدنية المصرية Wuzarah al-Bitrul wa ats-Tsarwah al-Ma'daniyyah al-Mishriyyah) adalah kementerian dalam Pemerintah Mesir yang membidangi urusan eksplorasi, produksi, pemasaran dan distribusi minyak, gas dan sumber daya alam lainnya. BUMN dibawah Kementerian Egyptian General P...

 

Unione Sportiva Livorno 1941-1942

Voce principale: Unione Sportiva Livorno 1915. Unione Sportiva LivornoStagione 1941-1942Sport calcio Squadra Livorno Allenatore József Viola Presidente Bruno Baiocchi Serie A14º posto. Maggiori presenzeCampionato: Capaccioli, Michelini (29)Totale: Capaccioli, Michelini (31) Miglior marcatoreCampionato: Viani II (10)Totale: Viani II (13) StadioStadio Edda Ciano Mussolini 1940-1941 1942-1943 Si invita a seguire il modello di voce Questa voce raccoglie le informazioni riguardanti l'Union...

Meat pie (Australia and New Zealand)

Pie containing diced or minced meat and gravy Meat pieA typical meat pie with tomato sauceTypeMeat piePlace of originAustralia and New ZealandMain ingredientsDiced or minced meat, gravy  Media: Meat pie In Australia and New Zealand, a meat pie is a hand-sized pie containing diced or minced meat and gravy, sometimes with onion, mushrooms, or cheese and is often consumed as a takeaway food snack. This variant of the standard meat pie is considered iconic.[1] It was described by...

 

Équipe de Belgique masculine de cyclisme sur route

Cet article est une ébauche concernant le cyclisme et la Belgique. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. L'équipe de Belgique masculine de cyclisme sur route est la sélection de cyclistes belges, réunis lors de compétitions internationales (les championnats d'Europe, du monde et les Jeux olympiques notamment) sous l'égide de la Royale ligue vélocipédique belge. Le sélectionneur est Sven Vantho...