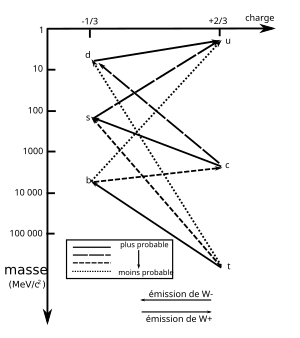
Quark étrange
|
Read other articles:

Genus of flowering plants Cedrela Cedrela odorata foliage Scientific classification Kingdom: Plantae Clade: Tracheophytes Clade: Angiosperms Clade: Eudicots Clade: Rosids Order: Sapindales Family: Meliaceae Subfamily: Cedreloideae Genus: CedrelaP.Browne Type species Cedrela odorataL. Species See text Cedrela is a genus of several species in the mahogany family, Meliaceae.[1] They are evergreen or dry-season deciduous trees with pinnate leaves, native to the tropical and subtropical Ne...

Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber: Rumah Sakit Santosa – berita · surat kabar · buku · cendekiawan · JSTOR Rumah Sakit Swasta Santosa atau lebih dikenal dengan RS Santosa adalah sebuah rumah sakit swasta yang berada di Kota Bandung, Jawa ...

1964 AFC Asian CupAsian Cup Israel 1964גביע אסיה בכדורגל 1964Israel holds the Asian Cup after winning itTournament detailsHost countryIsraelDates26 May – 3 JuneTeams4Venue(s)4 (in 4 host cities)Final positionsChampions Israel (1st title)Runners-up IndiaThird place South KoreaFourth place Hong KongTournament statisticsMatches played6Goals scored13 (2.17 per match)Attendance99,000 (16,500 per match)Top scorer(s) Inder Singh Mordechai Spi...

For the place, see Ragnall. RagnallRaghnall in a Gaelic type, note the lenited g in the name (gh) once appeared in Irish orthography with a dot above it, as pictured.GenderMasculineLanguage(s)Old Irish, Middle Irish/Middle GaelicOriginLanguage(s)Old NorseWord/nameRøgnvaldr, Rǫgnvaldr, RögnvaldrDerivationregin + valrMeaning(German) Gods, powerfulOther namesCognate(s)see listDerivative(s)Raghnall, Raonall, Raonull Ragnall, Raghnall, Raonall, and Raonull are masculine personal names or given ...

2012 mobile strategy game This article needs to be updated. Please help update this article to reflect recent events or newly available information. (June 2023) 2012 video gameClash of ClansDeveloper(s)SupercellPublisher(s)SupercellPlatform(s)iOSiPadOSAndroidReleaseiOSAugust 2, 2012 (2012-08-02)[1]AndroidOctober 7, 2013 (2013-10-07)[2]Genre(s)StrategyMode(s)Single-player, multiplayer Clash of Clans is a 2012 free-to-play mobile strategy video game...

Pelabuhan Chiba千葉港Pemandangan arah tenggara dari menara Pelabuhan ChibaLokasiNegaraJepangLokasiPrefektur ChibaKoordinat35°36′27″N 140°06′14″E / 35.607627°N 140.103836°E / 35.607627; 140.103836DetailMulai beroperasi1953OperatorPrefektur ChibaLuas lahan246,85 kilometer persegi (24.685 ha)StatistikKedatangan kapal65,200Tonase kargo per tahun166,964,000 metrik tonVolume peti kemas per tahun41,780 TEUs (TEU)Situs webhttp://www.pref.chiba.lg....

Biélorussieau Concours Eurovision 2021 Données clés Pays Biélorussie Chanson Ya Nauchu Tebya Interprète Galasy ZMesta Langue Russe Sélection nationale Radiodiffuseur BTRC Type de sélection Sélection interne Concours Eurovision de la chanson 2021 2020 (édition annulée)2019 modifier La Biélorussie était l'un des quarante pays participants du Concours Eurovision de la chanson 2021, qui se déroule à Rotterdam, aux Pays-Bas. Le pays aurait du être représenté par le groupe G...

American record charts Logo of Rolling Stone magazine The Rolling Stone charts tabulated the relative weekly popularity of songs and albums in the United States. Chart data was powered by analytics firm Alpha Data (formerly BuzzAngle Music) and results were published on the website of pop culture magazine Rolling Stone, both of which are properties of the United States-based Penske Media Corporation (PMC). The Rolling Stone charts competed with the Billboard charts, which are powered by Niels...

This article does not cite any sources. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Incontro con Mina – news · newspapers · books · scholar · JSTOR (December 2012) (Learn how and when to remove this template message) 1969 compilation album by MinaIncontro con MinaCompilation album by MinaReleased1969Length49:30LabelPDUMina chronology Mina for You(1969) ...

DIII-DA worker inside the DIII-D vesselDevice typeTokamakLocationSan Diego, California, USAffiliationGeneral AtomicsTechnical specificationsMajor radius1.67 m (5 ft 6 in)Minor radius0.67 m (2 ft 2 in)Magnetic field2.2 T (22,000 G) (toroidal)Heating power23 MWPlasma currentup to 2.0 MAHistoryYear(s) of operation1986–presentPreceded byDoublet III DIII-D is a tokamak that has been operated since the late 1980s by General Atomics (GA) in San Die...

ХристианствоБиблия Ветхий Завет Новый Завет Евангелие Десять заповедей Нагорная проповедь Апокрифы Бог, Троица Бог Отец Иисус Христос Святой Дух История христианства Апостолы Хронология христианства Раннее христианство Гностическое христианство Вселенские соборы Н...

United States historic placeNotre Dame SchoolU.S. National Register of Historic Places Show map of MassachusettsShow map of the United StatesLocationFall River, MassachusettsCoordinates41°41′28″N 71°8′2″W / 41.69111°N 71.13389°W / 41.69111; -71.13389Built1899ArchitectLouis G. DestrempsArchitectural styleColonial RevivalMPSFall River MRANRHP reference No.83000697[1]Added to NRHPFebruary 16, 1983 Notre Dame School is a historic former s...

B.26 Botha Blackburn B.26 Botha Role Torpedo bomberType of aircraft Manufacturer Blackburn Aircraft First flight 28 December 1938 Introduction 12 December 1939 Retired September 1944 Primary user Royal Air Force Number built 580 The Blackburn B.26 Botha was a four-seat reconnaissance and torpedo bomber. It was produced by the British aviation company Blackburn Aircraft at its factories at Brough and Dumbarton. The Botha was developed during the mid 1930s in response to Air Ministry Spec...
周處除三害The Pig, The Snake and The Pigeon正式版海報基本资料导演黃精甫监制李烈黃江豐動作指導洪昰顥编剧黃精甫主演阮經天袁富華陳以文王淨李李仁謝瓊煖配乐盧律銘林孝親林思妤保卜摄影王金城剪辑黃精甫林雍益制片商一種態度電影股份有限公司片长134分鐘产地 臺灣语言國語粵語台語上映及发行上映日期 2023年10月6日 (2023-10-06)(台灣) 2023年11月2日 (2023-11-02)(香�...

Ideas from Mathematics have been used as inspiration for fiber arts A Möbius strip scarf made from crochet. Ideas from mathematics have been used as inspiration for fiber arts including quilt making, knitting, cross-stitch, crochet, embroidery and weaving. A wide range of mathematical concepts have been used as inspiration including topology, graph theory, number theory and algebra. Some techniques such as counted-thread embroidery are naturally geometrical; other kinds of textile provide a ...

Частина серії проФілософіяLeft to right: Plato, Kant, Nietzsche, Buddha, Confucius, AverroesПлатонКантНіцшеБуддаКонфуційАверроес Філософи Епістемологи Естетики Етики Логіки Метафізики Соціально-політичні філософи Традиції Аналітична Арістотелівська Африканська Близькосхідна іранська Буддій�...

Dialects and varieties of the Greek language spoken in the modern era This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Modern Greek – news · newspapers · books · scholar · JSTOR (March 2019) (Learn how and when to remove this message) Modern GreekΝέα ΕλληνικάPronunciation[ˈne.a eliniˈka]N...

Stadium in Canberra, Australia GIO Stadium CanberraFormer namesCanberra StadiumBruce StadiumNational Athletics StadiumLocationBruce, Australian Capital TerritoryCoordinates35°15′0″S 149°6′10″E / 35.25000°S 149.10278°E / -35.25000; 149.10278OwnerAustralian Sports CommissionCapacity25,011[1]Record attendance28,753 – Brumbies vs Crusaders, 2004 Super 12 FinalSurfaceGrassConstructionOpened29 October 1977ArchitectPhilip CoxMain contractorsLeighton Cont...

This article's lead section may be too short to adequately summarize the key points. Please consider expanding the lead to provide an accessible overview of all important aspects of the article. (December 2015) 7th episode of the 8th season of How I Met Your Mother The Stamp TrampHow I Met Your Mother episodeEpisode no.Season 8Episode 7Directed byPamela FrymanWritten byTami SagherOriginal air dateNovember 19, 2012 (2012-11-19)Guest appearances Joe Manganiello as Brad Joe ...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada November 2022. BiaBia, 2017Informasi latar belakangNama lahirBianca Miquela LandrauNama lainPerico Princess[1]Lahir16 Agustus 1991 (umur 32)[2]Medford, Massachusetts, A.S.GenreHip hopPekerjaanRapperTahun aktif2012–sekarangLabel Epic I Am Other...