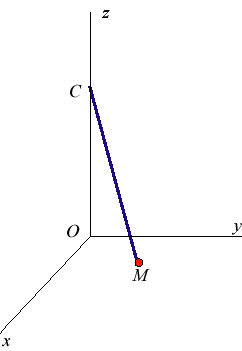
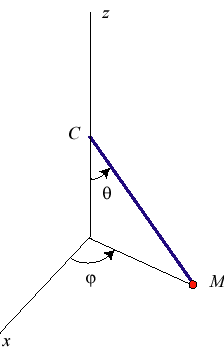
Pendule sphérique
|
Read other articles:

Niles adalah sebuah kota di negara bagian Ohio, Amerika Serikat, yang secara administratif terletak di Trumbull County. Demografi Menurut sensus tahun 2000 jumlah penduduk kota ini mencapai 20.932. Pada tahun 2006 menurut United States Census Bureau penduduknya menurun sebanyak 1108 jiwa (-5,3%) menjadi 19.824. Geografi Menurut United States Census Bureau kota ini memiliki wilayah permukaan 22,2 km², di mana 22,2 km² berupa daratan dan 0,0 km² perairan. Tempat di sekitar Niles Berikut ini...

Layar pada Pekan Olahraga Nasional 2021LokasiPantai Hamadi TNI AL, JayapuraTanggal3–12 Oktober 2021← 20162024 → Medali Perolehan medali * Tuan rumah penyelenggara (Papua)PeringkatProvinsiEmasPerakPerungguTotal1 Kalimantan Timur52292 Banten30253 Daerah Khusus Ibukota Jakarta25074 Kepulauan Riau23055 Jawa Timur21476 Papua*20247 Bali10018 Jawa Barat03479 Kalimantan Utara0101 Lampung0101 Pa...

Comics character Andrew BennettCover of The House of Mystery #290 (March 1981), art by Joe Kubert.Publication informationPublisherDC ComicsFirst appearanceThe House of Mystery #290 (March, 1981)Created byJ. M. DeMatteis (writer)Tom Sutton (artist)In-story informationFull nameAndrew BennettTeam affiliationsJustice League DarkTeam 13Justice LeagueAbilitiesTraditional vampiric attributes such as immortality and healing, superhuman strength and speed, heightened senses (including night vision), h...

العلاقات الألبانية الإكوادورية ألبانيا الإكوادور ألبانيا الإكوادور تعديل مصدري - تعديل العلاقات الألبانية الإكوادورية هي العلاقات الثنائية التي تجمع بين ألبانيا والإكوادور.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية للدو�...

البعثات الدبلوماسية اليمنية هذه قائمة البعثات الدبلوماسية اليمنية، باستثناء القنصليات الفخرية.[1] أوروبا سفارة اليمن في باريس سفارة اليمن في براغ عاصمة جمهورية التشيك سفارة اليمن في وارسو، بولندا النمسا فيينا (سفارة) بلجيكا بروكسل (سفارة) بلغاريا صوفيا (سفار...

Recopa Sudamericana 2022 Competizione Recopa Sudamericana Sport Calcio Edizione 30ª Organizzatore CONMEBOL Date 23 febbraio e 2 marzo 2022 Partecipanti 2 Risultati Vincitore Palmeiras(1º titolo) Secondo Athl. Paranaense Statistiche Incontri disputati 2 Gol segnati 6 (3 per incontro) Cronologia della competizione 2021 2023 Manuale La Recopa Sudamericana 2022 è stata la trentesima edizione della Recopa Sudamericana. La competizione ha opposto, con partite di andata e ritorn...

American television network (1978–2021) Television channel WGN AmericaCountryUnited StatesBroadcast areaNationwideNetworkThe WB (1995–1999)HeadquartersChicago, IllinoisProgrammingLanguage(s)EnglishPicture format1080i (HDTV)(downscaled to letterboxed 480i for the SDTV feed)OwnershipOwnerTribune Media (1978–2019)Nexstar Media Group (2019–2021)ParentDT Media GroupSister channels WGN-TV WGN (AM) Antenna TV HistoryLaunchedNovember 9, 1978 (1978-11-09)[1][2]Cl...

ХристианствоБиблия Ветхий Завет Новый Завет Евангелие Десять заповедей Нагорная проповедь Апокрифы Бог, Троица Бог Отец Иисус Христос Святой Дух История христианства Апостолы Хронология христианства Раннее христианство Гностическое христианство Вселенские соборы Н...

ХристианствоБиблия Ветхий Завет Новый Завет Евангелие Десять заповедей Нагорная проповедь Апокрифы Бог, Троица Бог Отец Иисус Христос Святой Дух История христианства Апостолы Хронология христианства Раннее христианство Гностическое христианство Вселенские соборы Н...

1988 studio album by SanctuaryRefuge DeniedStudio album by SanctuaryReleased1988StudioSteve Lawson (Seattle)Genre Heavy metal[1] thrash metal[2] power metal[3] Length39:35LabelEpicProducerDave Mustaine, Paul LaniSanctuary chronology Refuge Denied(1988) Into the Mirror Black(1990) Professional ratingsReview scoresSourceRatingAllMusic[2]BillboardUnfavorable[4]Hollywood Metal7/9[5]Rock Hard9/10[6] Refuge Denied is the debut studio a...

وادي فوكين الإحداثيات 31°42′24″N 35°06′14″E / 31.706666666667°N 35.103888888889°E / 31.706666666667; 35.103888888889 تقسيم إداري البلد دولة فلسطين[1] التقسيم الأعلى محافظة بيت لحم خصائص جغرافية ارتفاع 650 متر رمز جيونيمز 281356 تعديل مصدري - تعديل منظر عام لقرية وادي ف...

Baltic independence movements (1987–1991) This article is about the revolution in the Baltic states in the late 1980s. For the 2006 film about the revolution in the Baltic states, see The Singing Revolution. Singing RevolutionPart of the Revolutions of 1989 and the Dissolution of the Soviet UnionThe Baltic Way human chain in 1989Date14 June 1987 – 6 September 1991 (1987-06-14 – 1991-09-06)(4 years, 2 months, 3 weeks and 2 days)Locat...

Pour les articles homonymes, voir Van Beneden. Édouard Van Beneden Édouard Van Beneden Données clés Naissance 5 mars 1846Louvain (Belgique) Décès 28 avril 1910Liège (Belgique) Nationalité Belgique Données clés Domaines zoologiste, embryologiste Institutions Université de Liège Renommé pour Découverte de la méiose Distinctions Prix quinquennal des Sciences en 1871, 1887 et 1891 modifier Édouard Joseph Louis Marie Van Beneden, né à Louvain le 5 mars 1846 et mort à Liège le ...
Questa voce sull'argomento cestisti tedeschi è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Joshiko SaibouNazionalità Germania Altezza188 cm Peso82 e 80 kg Pallacanestro RuoloPlaymaker Squadra Science City Jena CarrieraGiovanili 1997-2000BSC Berlino2000-2006 TuS Lichterfelde2006-2007Mount Si High School2007-2010 Alba Berlino Squadre di club 2010-2011 Alba Berlino2 (0)2011-201...

1915 German offensive on the Eastern Front of World War I Gorlice–Tarnów offensivePart of the Eastern Front of World War IGorlice–Tarnów breakthroughand Russian withdrawalDate2 May – 13 July 1915LocationGorlice and Tarnów area, south-east of Kraków, Galicia, Austria-Hungary (present-day Poland)Result Central Powers victory Great RetreatBelligerents German Empire Austria-Hungary Russian EmpireCommanders and leaders Erich von Falkenhayn August von Mackensen Hans von Seeckt ...

Type of reed pen used for Islamic and Sephardic Jewish calligraphy For other uses, see Qalam (disambiguation). Not to be confused with Kalam. Qalams as used in calligraphy. A qalam (Arabic: قلم) is a type of reed pen. It is made from a cut, dried reed, and used for Islamic calligraphy. The pen is seen as an important symbol of wisdom in Islam, and references the emphasis on knowledge and education within the Islamic tradition. Etymology The word was borrowed from Greek kálamos (κάλαμ...

1935–1937 war between Italy and Ethiopia For other wars between Italy and Ethiopia, see Italo-Ethiopian war (disambiguation). Second Italo-Ethiopian WarPart of the interwar periodClockwise from top left: Italian Blackshirts at Dire Dawa; Ethiopian soldiers on horseback; Italian artillery in Tembien; Ethiopian soldiers holding rifles en route to the northern front; Royal Italian Army soldiers in Amba Aradam; Haile Selassie with Red Cross members.Date3 October 1935 – 19 February 1937[a&...

Éclipse partielle de Lunedu 17 octobre 2005 Depuis Taipei (Taïwan), 12 h 4 UTC. Schéma de l'évolution de l'éclipse, tandis que la Lune passe de droite (Ouest) à gauche (Est) dans l'ombre de la Terre. Gamma 0,9796 Magnitude 0,068 Localisation Océan Pacifique, Asie, Australie, Amérique du Nord Saros (membre de la série) 146 (10 sur 72) Durée (h:min:s) Phases partielles 55 min 58 s Phases pénombrales 4 h 19 min 49 s Contacts (UTC) P1 9:53:27 U1 11:35:18 Maximum 12:03:22 U4 ...

Coppa del Generalísimo 1964-1965Copa del Generalísimo 1964-1965 Competizione Copa del Rey Sport Calcio Edizione 61ª Organizzatore RFEF Date 15 novembre 1964 - 4 luglio 1965 Luogo Spagna Partecipanti 48 Risultati Vincitore Atlético Madrid(3º titolo) Secondo Real Saragozza Semi-finalisti Athletic Bilbao Real Sociedad Cronologia della competizione 1963-1964 1965-1966 Manuale La Copa del Generalísimo 1964-1965 fu la 61ª edizione della Coppa di Spagna. Il torne...

Austrian footballer This article is about the footballer. For the alpine skier, see Johannes Aigner (alpine skier). Hannes Aigner Aigner with Wiener Neustadt in 2014Personal informationDate of birth (1981-03-16) 16 March 1981 (age 43)Place of birth Schwaz, Tirol, AustriaHeight 1.86 m (6 ft 1 in)Position(s) StrikerYouth career SV WeerbergSenior career*Years Team Apps (Gls)1996–2000 SV Weerberg 2000–2002 Innsbrucker SK 2002–2006 FC Wacker Tirol 79 (11)2006–2008 Austr...