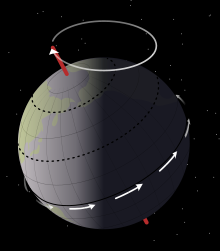
Précession
|
Read other articles:

Ini adalah nama Tionghoa; marganya adalah Ni. Ni KuangNi Kuang di Universitas Shue Yan Hong Kong, November 2007Nama asalHanzi: 倪匡Lahir(1935-05-30)30 Mei 1935Ningbo, Zhejiang, Republik TiongkokMeninggal3 Juli 2022(2022-07-03) (umur 87)Hong KongPekerjaanNovelis, penulis skenario, aktorKarier menulisPeriode1956–2005GenreWuxia, fiksi ilmiah Ni Kuang Hanzi: 倪匡 Alih aksara Mandarin - Hanyu Pinyin: Ní Kuāng Yue (Kantonis) - Jyutping: Ngai4 Hong1 Ni Cong(birth name) Hanzi tr...

Duta Besar Amerika SerikatSegel Kementerian Dalam Negeri Amerika SerikatPetahanaLowongDicalonkan olehPresiden Amerika SerikatDitunjuk olehPresidendengan nasehat SenatPejabat perdanaUlysses Grant-Smithsebagai Duta Luar Biasa dan Menteri Berkuasa PenuhDibentuk22 September 1922Situs webU.S. Embassy - Tirana Berikut ini adalah daftar duta besar Amerika Serikat untuk Albania. Duta Besar Ulysses Grant-Smith Charles C. Hart Herman Bernstein Post Wheeler Hugh Gladney Grant William Edwin Ryerson Josep...

Часть серии статей о Холокосте Идеология и политика Расовая гигиена · Расовый антисемитизм · Нацистская расовая политика · Нюрнбергские расовые законы Шоа Лагеря смерти Белжец · Дахау · Майданек · Малый Тростенец · Маутхаузен ·&...

Sporting event delegationPakistan at the2008 Summer OlympicsIOC codePAKNOCNational Olympic Committee of PakistanWebsitenocpakistan.orgin BeijingCompetitors21 in 4 sportsFlag bearer Zeeshan AshrafMedals Gold 0 Silver 0 Bronze 0 Total 0 Summer Olympics appearances (overview)19481952195619601964196819721976198019841988199219962000200420082012201620202024 Pakistan competed at the 2008 Summer Olympics in Beijing, China. The country sent 21 athletes, including two women (Sadaf Siddiqui in athl...

Anjungan Kota Semarang adalah salah satu Anjungan Daerah di Taman Mini Jawa Tengah (Puri Maerokoco). Anjungan ini menampilkan beberapa arsitektur rumah adat di Jawa Tengah salah satunya rumah adat khas Kota Semarang. Bangunan – bangunan dalam anjungan Kota Semarang terdiri atas Rumah adat Kota Semarang, Replika Tugu Muda, dll. Rumah Adat Kota Semarang Rumah Adat Kota Semarang memiliki bentuknya khas, yang merupakan perpaduan gaya dari budaya melayu dan eropa. Replika Tugu Muda Gerobogan ter...

This template was considered for deletion on 2019 August 14. The result of the discussion was keep. Radio Stations Template‑class Radio portalThis template is within the scope of WikiProject Radio Stations, a collaborative effort to improve the coverage of radio stations on Wikipedia. If you would like to participate, please visit the project page, where you can join the discussion and see a list of open tasks.Radio StationsWikipedia:WikiProject Radio StationsTemplate:WikiProject Radio Stat...

此條目可参照英語維基百科相應條目来扩充。 (2021年5月6日)若您熟悉来源语言和主题,请协助参考外语维基百科扩充条目。请勿直接提交机械翻译,也不要翻译不可靠、低品质内容。依版权协议,译文需在编辑摘要注明来源,或于讨论页顶部标记{{Translated page}}标签。 约翰斯顿环礁Kalama Atoll 美國本土外小島嶼 Johnston Atoll 旗幟颂歌:《星條旗》The Star-Spangled Banner約翰斯頓環礁�...
2020年夏季奥林匹克运动会马来西亚代表團马来西亚国旗IOC編碼MASNOC马来西亚奥林匹克理事会網站olympic.org.my(英文)2020年夏季奥林匹克运动会(東京)2021年7月23日至8月8日(受2019冠状病毒病疫情影响推迟,但仍保留原定名称)運動員30參賽項目10个大项旗手开幕式:李梓嘉和吳柳螢(羽毛球)[1][2]閉幕式:潘德莉拉(跳水)[3]獎牌榜排名第74 金牌 銀牌 銅�...

Danish men's handball team See also: SønderjyskE Damehåndbold SønderjyskEFull nameSønderjysk Elitesport HerrehåndboldShort nameSE, SønderjyskEFounded2004ArenaBroager Sparekasse SkansenCapacity2,200PresidentKlaus B. RasmussenHead coachRasmus Glad VandbækLeagueHerrehåndboldligaen2021–229th Home Away Website Official site SønderjyskE Herrehåndbold is a Danish men's handball club based in Sønderborg. They currently compete in the Danish Handball League and Danish Handb...

Logo dari Final Fantasy VI Final Fantasy VI (ファイナルファンタジーVIcode: ja is deprecated , Fainaru Fantajī Shikkusu) adalah role-playing game yang dikembangkan dan diproduksi oleh Square Co., Ltd. tahun 1994 untuk konsol permainan Super Famicom. Ia disutradarai oleh Yoshinori Kitase dan Hiroyuki Itō, yang menggantikan pencipta dan produser seri Final Fantasy Hironobu Sakaguchi, yang mensutradarai lima judul sebelumnya. Lagu dan musiknya disusun oleh kontributor kawakan seri FF...

Музыка горячей водыHot Water Music Автор Чарльз Буковски Жанр Грязный реализм Язык оригинала американский английский Оригинал издан 1983 Переводчик Максим Немцов Издатель ЭксмоBlack Sparrow Books[англ.] Страниц 302 ISBN 978-5-699-51194-5 «Музыка горячей воды» (англ. Hot Water Music) — сборник р�...

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (ديسمبر 2018) دوري كندا لكرة القدم الجهة المنظمة اتحاد كندا لكرة القدم تاريخ الإنشاء 2008 الرياضة كرة القدم البلد ...

Bishop of Valladolid Manuel Abad y QueipoBishop-electDioceseMichoacán, MéxicoInstalled1810 (not confirmed)Term ended1822PredecessorMarcos de Moriana y ZafrillaSuccessorJuan Cayetano Gómez de Portugal y SolísPersonal detailsBorn(1751-08-26)26 August 1751Villarpedre, AsturiasDied15 September 1825(1825-09-15) (aged 74)Toledo, SpainNationalitySpanishDenominationRoman Catholic Manuel Abad y Queipo (26 August 1751 – 15 September 1825) was a Spanish Roman Catholic Bishop of Michoacán in ...

Peta infrastruktur dan tata guna lahan di Komune Blennes. = Kawasan perkotaan = Lahan subur = Padang rumput = Lahan pertanaman campuran = Hutan = Vegetasi perdu = Lahan basah = Anak sungaiBlennesNegaraPrancisArondisemenFontainebleauKantonLorrez-le-Bocage-PréauxAntarkomunetidak ada pada 2007Pemerintahan • Wali kota (2008-2014) François Canterini • Populasi1477Kode INSEE/pos77035 / 2 Population sans doubles comptes: ...

Jessica AureliaLahirJessica Aurelia24 November 1988 (umur 35) Jakarta, DKI Jakarta, IndonesiaPekerjaanmodelTahun aktif2007–sekarang Jessica Aurelia (lahir 11 Desember 1988) adalah seorang model dan pengusaha Indonesia.[1] Ia meraih gelar Miss Indonesia Earth Air (sering disebut sebagai runner-up I) pada ajang Miss Indonesia Earth 2010[2] dan kemudian mewakili Indonesia dalam Miss Earth 2010.[3] Pendidikan Universitas Pelita Harapan (2005–2009)[4]...

2019 Indian general election in Goa ← 2014 23 April 2019 2024 → 2 seatsTurnout75.14% (1.92%) First party Second party Third party Party BJP INC AAP Alliance NDA UPA Last election 2 0 0 Seats won 1 1 0 Seat change 1 1 Percentage 51.19% 42.92% 3.01% Swing 2% 6.3% 3% 2019 Indian general election in Goa The 2019 Indian general election was held in India between April and May 2019 to constitute the 17th Lok Sabha.[1] Candidates Major elec...

郭懺个人资料出生1894年4月18日逝世1950年7月31日(1950歲—07—31)(56歲)死因腦溢血墓地新北市淡水區籍贯浙江諸暨国籍 大清(1894年–1911年) 中華民國(1912年–1926年) 中華民國(1926年–1950年)政党 中國國民黨 郭懺(1894年4月18日—1950年7月31日)[1],字悔吾,浙江諸暨东山吴人,畢業於保定軍校第六期砲兵科,在國民革命軍派系中屬於陳誠系之將領。...

Nie 31 Nieuport 31 circa 1919 Role Single-seat fighterType of aircraft National origin France Manufacturer Nieuport First flight 1919 Status Abandoned Number built 2[1] Developed from Nieuport Madon The Nieuport Nie 31 or Nieuport 31 was a single-engine, single-seat monoplane or sesquiplane fighter aircraft designed and built in France in 1919. Design and development Though the Nie 31 (it had been flown and subsequently abandoned before the company changed its name to Nieuport-Delage...

日本の政治家小池 百合子こいけ ゆりこ 内閣広報室より公表された肖像生年月日 (1952-07-15) 1952年7月15日(72歳)出生地 日本 兵庫県出身校 カイロ大学文学部社会学科卒業[1][2][3]前職 ニュースキャスターアラビア語通訳現職 東京都知事所属政党 (日本新党→)(新進党→)(自由党→)(保守党→)(保守クラブ→)(自由民主党〈清和会→無派閥〉�...

Australian rules footballer Australian rules footballer Jack Bisset Bisset on a Hoadleys' trading card, 1933Personal informationFull name John James BissetDate of birth (1900-09-01)1 September 1900Place of birth Longwarry, VictoriaDate of death 21 August 1966(1966-08-21) (aged 65)Place of death Caulfield, VictoriaOriginal team(s) Nar Nar Goon (EDFL)Port Melbourne (VFA)Stawell (WFL)Height 180 cm (5 ft 11 in)Weight 83 kg (183 lb)Playing career1Years Club Games...