Matrice densité
|
Read other articles:

Districts of Andhra Pradesh. Distrik Anantapur adalah distrik yang terletak di negara bagian Andhra Pradesh, India. Distrik ini dibentuk pada tahun 1882. Distrik Anantapur merupakan distrik terluas di Andhra Pradesh dengan luas 19.130 km². Berbatasan dengan Distrik Kadapa di bagian timur, Distrik Chitttoor dan Karnataka di bagian barat. Jumlah penduduknya 36.040.478 jiwa pada tahun 2001. Demografi Agama Agama di distrik Anantapur (2011)[1] Hindu (88.20%) Islam ...

British and South African judge (born 1934) The Right HonourableThe Lord HoffmannGBS PCHoffmann in 2018Second Senior Lord of Appeal in OrdinaryIn office10 January 2007 – 21 April 2009MonarchElizabeth IIPreceded byThe Lord Nicholls of BirkenheadSucceeded byThe Lord Hope of CraigheadLord of Appeal in OrdinaryIn office21 February 1995 – 21 April 2009Succeeded byThe Lord Collins of MapesburyNon-Permanent Judge of the Court of Final Appeal of Hong KongIncumbentAssumed office&...

العلاقات الصومالية المالطية الصومال مالطا الصومال مالطا تعديل مصدري - تعديل العلاقات الصومالية المالطية هي العلاقات الثنائية التي تجمع بين الصومال ومالطا.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية للدولتين: وجه المقارنة ا�...

Peer-reviewed academic journal Academic journalThe English Historical ReviewDisciplineHistoryLanguageEnglishEdited byNandini ChatterjeeStephen ConwayPeter MarshallJan RügerHannah SkodaAlice TaylorPublication detailsHistory1886–presentPublisherOxford University PressFrequencyBimonthlyImpact factor0.655 (2020)Standard abbreviationsISO 4 (alt) · Bluebook (alt1 · alt2)NLM (alt) · MathSciNet (alt )ISO 4Engl. Hist. Rev.IndexingCODEN (alt ·...

Short British and Irish television channel This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Nicktoonsters – news · newspapers · books · scholar · JSTOR (Feb...

United States historic placeAlbion Historic DistrictU.S. National Register of Historic PlacesU.S. Historic district LocationLincoln, Rhode IslandBuilt1830Architectural styleItalianate, Queen AnneNRHP reference No.84001899[1]Added to NRHPJuly 19, 1984 Albion is a village and historic district in Lincoln, Rhode Island, in the United States. Albion is home to several mill buildings, churches, and the Kirkbrae Country Club golf course. The historic Blackstone River flows t...

Hollow body guitar by Gibson, 1961 to 1974 Barney Kessel1964 Gibson Barney Kessel customManufacturerGibson BrandsPeriod1961–1974ConstructionBody typeSemi-hollow body thinlineScale25 1/2WoodsBodySpruce and MapleNeckMahoganyFretboardBrazilian rosewoodHardwareBridgeRosewoodPickup(s)HumbuckersColors availableSunburst The Gibson Barney Kessel (1961–1974) is a signature model guitar manufactured by the Gibson Guitar Company. The guitar was a signature model for the popular Jazz musician Barney...

Hong Kong pop singer This article is about the Hong Kong singer. For the philanthropist, see Priscilla Chan. For the Singaporean actress, see Priscelia Chan. In this Chinese name, the family name is Chan (陳). Priscilla Chan Wai-han陳慧嫻Chan during the PolyGram Forever Live Concert in Singapore at the Singapore Indoor Stadium, 2014Background informationBirth nameChan Wai-han (陳慧嫻)Also known asWai-han (慧嫻)PCPriscillaPrincess (公主)Hatted Diva (帽子天后)Iron-lung Lady (鐵�...

Questa voce sull'argomento sovrani cinesi è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Sui YangdiImperatore della dinastia SuiIn carica21 agosto 604 –11 aprile 618 PredecessoreSui Wendi SuccessoreYang You Nome templareShizu 世祖 Nomi postumiDinastia Tang: Yang 煬, l'indolente Yang Tong: Ming 明, il comprensivo Dou Jiande: Min 閔, l'attento Altri titoliYang Guang 楊廣 Nascita569 MorteDanyang, 11 aprile 618 Luogo di sepolturaJiang...

Indian materials physicist Kasturi Lal ChopraInaugurating a seminar at Rajiv Gandhi Technological UniversityDirector at Indian Institute of Technology KharagpurIn office1987–1997Preceded byG. S. SanyalSucceeded byAmitabha GhoshProfessor at Indian Institute of Technology DelhiIn office1970–1987 Personal detailsBorn (1933-07-31) 31 July 1933 (age 90)Chahal Kalan, Gujranwala District, Punjab Province, British IndiaDied18 May 2021SpouseAsha Suri ChopraChildren3OccupationAcademic, Materia...

1954 novel by Isaac Asimov The Caves of Steel Cover of first edition (hardcover)AuthorIsaac AsimovCover artistRuth Ray[1]CountryUnited StatesLanguageEnglishSeriesRobot seriesGenreMystery Science fictionPublisherDoubledayPublication date1953 (magazine), February 4, 1954 (book)[2]Media typePrint (Hardcover, Paperback)Pages224Preceded byMother EarthFollowed byThe Naked Sun The first instalment of Asimov's The Caves of Steel took the cover of the October ...

Scottish civil engineer and shipbuilder For other people named William Fairbairn, see William Fairbairn (disambiguation). Sir William FairbairnBt FRSby Benjamin Rawlinson Faulkner, in the foreground Observations of the Cold blast, referring to On the strength and properties of cast iron obtained from the Hot and Cold blast, presented at the British Association for the Advancement of Science in 1838[1]Born(1789-02-19)19 February 1789Kelso, ScotlandDied18 August 1874(1874-08-18) (aged&#...

Папий Иерапольский Дата рождения 70[1][2], I век[3] или около 60[4] Место рождения Малая Азия[d], Турция Дата смерти II век[3] или 140[4] Место смерти Смирна, Древний Рим или Измир[5] Страна Азия Род деятельности священник, писатель П�...
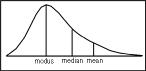
Data menyebar normal sehingga Median, Mean dan Modus relatif sama Data menjulur ke kanan sehingga Median, Mean dan Modus berbeda-beda Ukuran pemusatan data adalah sembarang ukuran yang menunjukkan pusat segugus data, yang telah diurutkan dari yang terkecil sampai yang terbesar atau sebaliknya dari yang terbesar sampai yang terkecil.[1] Salah satu kegunaan dari ukuran pemusatan data adalah untuk membandingkan dua (populasi) atau contoh, karena sangat sulit untuk membandingkan masing-ma...

Đế quốc La Mã dưới thời Hadrianus (trị vì 117—138), cho thấy vị trí của tộc German Burgundiones, khi đó cư ngụ vùng giữa sông Viadua (Oder) và Visula (Vistula) (Ba Lan ngày nay). Burgundi (tiếng Latinh: Burgundiōnes, Burgundī; tiếng Bắc Âu cổ: Burgundar; tiếng Anh cổ: Burgendas; tiếng Hy Lạp: Βούργουνδοι) là một bộ tộc, hay nhóm bộ tộc, German Đông hay Vandal, từng sống ở nơi ngày nay là Ba Lan vào t...

Ruling party of Rhodesia (1965–1979) Rhodesian Front AbbreviationRFLeaderIan SmithFounded1 March 1962 (1962-03-01)Dissolved6 June 1981 (1981-06-06)Preceded byDominion Party[1]Southern Rhodesia Liberal PartySucceeded byRepublican FrontHeadquartersSalisbury, RhodesiaIdeologyWhite minority interests[2]White supremacy[3][4][5]Rhodesian nationalism[6][7]National conservatism[8]Social conservat...

莎拉·阿什頓-西里洛2023年8月,阿什頓-西里洛穿著軍服出生 (1977-07-09) 1977年7月9日(46歲) 美國佛羅里達州国籍 美國别名莎拉·阿什頓(Sarah Ashton)莎拉·西里洛(Sarah Cirillo)金髮女郎(Blonde)职业記者、活動家、政治活動家和候選人、軍醫活跃时期2020年—雇主內華達州共和黨候選人(2020年)《Political.tips》(2020年—)《LGBTQ國度》(2022年3月—2022年10月)烏克蘭媒�...

Військово-музичне управління Збройних сил України Тип військове формуванняЗасновано 1992Країна Україна Емблема управління Військово-музичне управління Збройних сил України — структурний підрозділ Генерального штабу Збройних сил України призначений для планува...

Romanian Bangladesh Ethnic group Bangladeshi Romaniansরোমানীয় বাংলাদেশীTotal population1,674[1] (2022)Regions with significant populationsBucharest and other large urban areasLanguagesRomanian · Bangladeshi English · BengaliReligionSunni Islam (majority)Related ethnic groupsRomanian immigrants · Bangladeshi diaspora The Bangladesh Romanians (Bengali: রোমানীয় বাংলাদেশী) are a...

Para anggota gerakan bawah tanah Eindhoven bersama dengan pasukan dari Divisi Airborne ke-101 AS di Eindhoven pada Operasi Taman Pasar, September 1944 Gerakan bawah tanah Belanda terhadap pendudukan Nazi di Belanda saat Perang Dunia II umumnya dapat dikarakterisasikan oleh gerakan non-kekerasannya yang berpengaruh, yang jumlah anggotanya memuncak menjadi lebih dari 300,000 orang di persembunyian pada musim gugur 1944.[1] Definisi Orang-orang Belanda sendiri, khususnya sejarawan perang...
































![{\displaystyle [{\hat {H}},{\hat {\rho }}]=i\hbar {d \over dt}{\hat {\rho }}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/393e54482c993ffce8aa6670a24c9eff5b8d2010)






