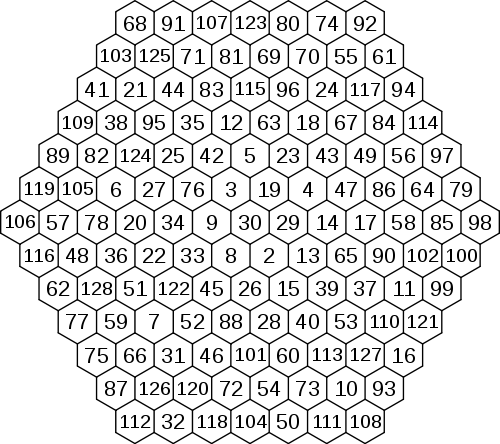
Hexagone magique

En mathématiques, un hexagone magique d'ordre n est un arrangement de nombres formant un gabarit hexagonal centré avec n cellules sur chaque côté. La somme des nombres dans chaque rangée ou dans les trois directions font la même somme. Un hexagone magique normal contient tous les entiers allant de 1 à 3n2 − 3n + 1. Il existe seulement deux arrangements respectant ces conditions, celui d'ordre 1 et celui d'ordre 3. De plus, la solution d'ordre 3 est unique[1]. Meng en donne une preuve constructive [2].

Hexagones normaux

Un hexagone magique est dit normal quand il utilise la suite des nombres commençant par 1.

Ordre 1 Ordre 3
M = 1 M = 38

L'hexagone d'ordre 3 a été publié à plusieurs reprises comme une « nouvelle » découverte. La plus vieille référence sur le sujet remonte à Ernst von Haselberg en 1887.

Hexagones non normaux

Il existe des hexagones non normaux d'ordre supérieur à 3. La suite numérique commence avec un nombre différent de 1, qui peut être positif ou négatif. Arsen Zahray a découvert ces hexagones d'ordre 4 et 5 :

Ordre 4 (non normal) Ordre 5 (non normal)
(commence à 3 et se termine à 39) (commence à 6 et se termine à 66)
M = 111 M = 244

Un hexagone d'ordre 6 a été publié par Louis Hoelbling le  :

Ordre 6 (non normal)
(commence à 21 et se termine à 111)
M = 546

Un hexagone d'ordre 7 a été publié par Arsen Zahray le (il a fait appel au recuit simulé) :

Ordre 7 (non normal)
(commence à 2 et se termine à 128)
M = 635

Un hexagone d'ordre 8 a été publié par Louis K. Hoelbling le  :

Ordre 8 (non normal)
(commence à -84 et se termine à 84)
M = 0

Un hexagone d'ordre 9 a été publié par Klaus Meffert le  :

Ordre 9 (non normal)
(commence à -108 et se termine à 108)
M = 0

Notes et références

  1. ↑ (en) C. W. Trigg, « A Unique Magic Hexagon », Recreational Mathematics Magazine, January-February 1964. Consulté le 2009-12-16.
  2. ↑ (en) [PDF] Meng, F. « Research into the Order 3 Magic Hexagon », Shing-Tung Yau Awards, October 2008. Consulté le 2009-12-16.

Bibliographie

  • (en) J. E. Baker et D. R. King, « The use of visual schema to find properties of a hexagon », Visual Mathematics, Vol. 5, Number 3, 2004.
  • (en) J. E. Baker et A. J. Baker, « The hexagon, nature's choice », Archimedes, Vol. 4, 2004.
v · m
Polygones et polyèdres magiques
Carrés magiques
Autres polygones magiques
Cubes magiques
Concepts associés de carrés

Read other articles:

Keluarga Djajadiningrat

Keluarga Djajadiningrat adalah keluarga priayi berkedudukan tinggi di Indonesia pada masa kolonial, yang anggotanya sering menjabat sebagai Bupati Serang di Banten, Hindia Belanda.[1][2] Terkenal karena pandangan barat dan kesetiaan mereka kepada penguasa Belanda selama masa kolonial, keluarga ini bagaimanapun juga berjuang di kedua pihak dalam Revolusi Indonesia (1945-1949).[3] Pangeran Mangkunegara VII dan K.P.A. Hoessein Djajadiningrat dengan istri mereka, Ratu Timu...

 

طريق القاهرة - الإسكندرية الصحراوي

طريق القاهرة الإسكندرية الصحراوي الطريق تجاه القاهرة قرب مدينة السادات اسم آخر طريق مصر الإسكندرية الصحراوي البلد مصر  تاريخ الافتتاح 1935 (منذ 89 سنة) التصنيف طريق حر المميزات الطول 220 كم الاتجاه جنوب - شمال النهاية جنوب الجيزة التقاطعات محور 26 يوليو، محور الضبعة، الطريق �...

 

Orlando Quevedo

Filipino prelate of the Catholic Church (born 1939) In this Philippine name, the middle name or maternal family name is Beltran and the surname or paternal family name is Quevedo. His EminenceOrlando B. QuevedoO.M.I., D.D.CardinalArchbishop of CotabatoProvinceCotabatoSeeCotabatoInstalled30 May 1998Term ended6 November 2018PredecessorPhilip Francis Smith, O.M.I.SuccessorAngelito LamponOther post(s)Cardinal-Priest of S. Maria Regina Mundi a Torre SpaccataOrdersOrdination5 June 1964Cons...

Alliterative Revival

See also: alliterative verse Resurgence of poetry using the alliterative verse form in Middle English between c. 1350 and 1500 The Alliterative Revival is a term adopted by literary historians to refer to the resurgence of poetry using the alliterative verse form in Middle English between c. 1350 and 1500. Alliterative verse was the traditional verse form of Old English poetry; the last known alliterative poem prior to the Revival was Layamon's Brut, which dates from around 1190. Scholarly op...

 

Melanie Klein

Pour les articles homonymes, voir Klein. Melanie KleinBiographieNaissance 30 mars 1882VienneDécès 22 septembre 1960 (à 78 ans)LondresNom de naissance Melanie ReizesNationalité Autrichienne, BritanniqueFormation Université de VienneActivité PsychanalysteEnfant Melitta SchmidebergAutres informationsMembre de Association psychanalytique hongroiseSociété britannique de psychanalyseBerliner Psychoanalytische Vereinigung (d)Influencée par Sigmund FreudSite web (en) www.melanie-k...

 

Синелобый амазон

Синелобый амазон Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:ЗавропсидыКласс:Пт�...

Drew University

Private university in Madison, New Jersey This article is about the private university in New Jersey. For the private medical institution in Los Angeles, see Charles R. Drew University of Medicine and Science. Drew UniversityFormer namesDrew Theological Seminary (1867–1928)Mottoδωρεὰν ἐλάβετε, δωρεὰν δότεMotto in EnglishFreely ye have received, freely give. (from Matthew 10:8 KJV)TypePrivate universityEstablished1867; 157 years ago (1867)Reli...

 

South Devon College

This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article relies excessively on references to primary sources. Please improve this article by adding secondary or tertiary sources. Find sources: South Devon College – news · newspapers · books · scholar · JSTOR (February 2008) (Learn how and when to remove this message) This article includes a li...

 

乌克兰总理

 烏克蘭總理Прем'єр-міністр України烏克蘭國徽現任杰尼斯·什米加尔自2020年3月4日任命者烏克蘭總統任期總統任命首任維托爾德·福金设立1991年11月后继职位無网站www.kmu.gov.ua/control/en/（英文） 乌克兰 乌克兰政府与政治系列条目 宪法 政府 总统 弗拉基米尔·泽连斯基 總統辦公室 国家安全与国防事务委员会 总统代表（英语：Representatives of the President of Ukraine） 总...

Stasiun Rejotangan

Stasiun Rejotangan D28 Stasiun Rejotangan pada tahun 2020Lokasi Jalan Raya Tulungagung-BlitarRejotangan, Rejotangan, Tulungagung, Jawa Timur 66293IndonesiaKoordinat8°7′17″S 112°5′2″E / 8.12139°S 112.08389°E / -8.12139; 112.08389Koordinat: 8°7′17″S 112°5′2″E / 8.12139°S 112.08389°E / -8.12139; 112.08389Ketinggian+116 mOperator KAI Commuter Letakkm 135+971 lintas Bangil-Blitar-Kertosono[1] Jumlah peron2 (satu peron ...

 

Theodoros Diligiannis

Greek politician Theodoros DeligiannisΘεόδωρος ΔηλιγιάννηςTheodoros Diligiannis, Prime Minister of GreecePrime Minister of GreeceIn office19 April 1885 – 30 April 1886 (o.s.)MonarchGeorge IPreceded byCharilaos TrikoupisSucceeded byDimitrios ValvisIn office24 October 1890 – 18 February 1892Preceded byCharilaos TrikoupisSucceeded byKonstantinos KonstantopoulosIn office31 May 1895 – 18 April 1897Preceded byNikolaos DeligiannisSucceeded byDimitr...

 

Game Over (TV series)

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Game Over TV series – news · newspapers · books · scholar · JSTOR (October 2013) (Learn how and when to remove this message) American TV series or program Game OverThe Smashenburn familyGenreAnimated sitcomCreated byDavid SacksVoices of Patrick Warburton L...

نوازي لو سيك

نوازي لو سيك    شعار الاسم الرسمي (بالفرنسية: Noisy-le-Sec)‏    الإحداثيات 48°53′27″N 2°27′13″E / 48.890833333333°N 2.4536111111111°E / 48.890833333333; 2.4536111111111 [1]  [2] تقسيم إداري  البلد فرنسا[3][4]  التقسيم الأعلى السين  [لغات أخرى]‏ (4 مارس 1790–1 يناير 1968)س�...

 

Piaggio Ape

Pour les articles homonymes, voir Ape. Si ce bandeau n'est plus pertinent, retirez-le. Cliquez ici pour en savoir plus. Cet article ne s'appuie pas, ou pas assez, sur des sources secondaires ou tertiaires (mars 2020). Pour améliorer la vérifiabilité de l'article ainsi que son intérêt encyclopédique, il est nécessaire, quand des sources primaires sont citées, de les associer à des analyses faites par des sources secondaires. Piaggio Ape Piaggio Ape 50 de 2010. Marque Piaggio Années ...

 

I Said Never Again (But Here We Are)

2005 single by Rachel Stevens I Said Never Again (But Here We Are)Single by Rachel Stevensfrom the album Come and Get It B-sideWaiting GameReleased3 October 2005 (2005-10-03)[1]Length3:26LabelPolydorSongwriter(s)Rob Davis, Jewels & StoneProducer(s)Jewels & StoneRachel Stevens singles chronology So Good (2005) I Said Never Again (But Here We Are) (2005) I Said Never Again (But Here We Are) is a song by English singer-songwriter Rachel Stevens. It was released on ...

Mononym

Individual who is known and addressed by a single name This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Mononym – news · newspapers · books · scholar · JSTOR (October 2022) (Learn how and when to remove this message) Plato, Greek philosopher A mononym is a name composed of only one word. An individual who is ...

 

Hemiola

Musical ratio of 3:2 In music, hemiola (also hemiolia) is the ratio 3:2. The equivalent Latin term is sesquialtera. In rhythm, hemiola refers to three beats of equal value in the time normally occupied by two beats. In pitch, hemiola refers to the interval of a perfect fifth. Etymology The word hemiola comes from the Greek adjective ἡμιόλιος, hemiolios, meaning containing one and a half, half as much again, in the ratio of one and a half to one (3:2), as in musical sounds.[1]...

 

Richmond Railway Bridge

Bridge in RichmondRichmond Railway BridgeRichmond Railway Bridge looking downstreamCoordinates51°27′36″N 0°18′49″W / 51.46°N 0.3136°W / 51.46; -0.3136CarriesNational Rail services operated by South Western RailwayCrossesRiver ThamesLocaleRichmondOther name(s)Richmond Windsor and Staines Railway Bridge[1]Maintained byNetwork RailHeritage statusGrade II listed structure[1]CharacteristicsDesignTruss arch bridgeMaterialSteelTotal length91.5 met...

Zevaquenabant

Chemical compound ZevaquenabantClinical dataOther namesS-MRI-1867; INV-101; MRI-1867Legal statusLegal status Investigational Identifiers IUPAC name (4S)-N-(1-Aminoethylidene)-5-(4-chlorophenyl)-4-phenyl-N′-[4-(trifluoromethyl)phenyl]sulfonyl-3,4-dihydropyrazole-2-carboximidamide CAS Number1998760-00-1PubChem CID155321421UNIIT7JYL5VB4HChemical and physical dataFormulaC25H21ClF3N5O2SMolar mass547.98 g·mol−1 Zevaquenabant (S-MRI-1867, INV-101, or MRI-1867) is an investigational small-m...

 

Hengelo (Overijssel)

Cet article est une ébauche concernant une localité néerlandaise. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Pour les articles homonymes, voir Hengelo. Hengelo Armoiries. Drapeau. La tour d'hôtel de ville Administration Pays Pays-Bas Province Overijssel Code postal 7550-7559 Indicatif téléphonique international +(31) Démographie Population 81 380 hab. Densité 1 317 hab./km2 Géog...