Fréquence fondamentale
|
Read other articles:

Rusli Marzuki SariaBiografiKelahiran26 Februari 1936 (88 tahun)Kamang Mudiak Data pribadiKelompok etnikOrang Minangkabau KegiatanPekerjaanPenyair Periode aktif1957 –Bekerja diHarian Haluan KeluargaPasangan nikahHanizar Musa (1963–) Orang tuaMardjuki Datuk Radjo Pangulu , Sarianun Penghargaan Penghargaan Penulis Asia Tenggara Rusli Marzuki Saria (lahir 26 Februari 1936)[1] adalah veteran pejuang kemerdekaan,[1][2] wartawan, sastrawan dan penyair...

Biara Iona, salah satu markas komunitas iona. Komunitas Iona adalah komunitas yang didirikan oleh George MacLeod pada tahun 1938.[1] Anggota komunitas Iona terdiri dari gabungan kaum awam dan klerus dalam Gereja di Skotlandia.[1] Komunitas Iona mengalami perkembangan pesat dari jumlah anggota yang masih sedikit hingga mencapai ratusan.[2] Anggota dari komunitas ini mencakup segala golongan usia.[2] Tujuan dari didirkannya komunitas Iona ini adalah untuk mendoro...

大手町連鎖型都市再生プロジェクト > 日本経済新聞社東京本社ビル 日本経済新聞社東京本社ビル 日本経済新聞社東京本社ビル施設情報所在地 東京都千代田区大手町一丁目3-7座標 北緯35度41分19.5秒 東経139度45分44.2秒 / 北緯35.688750度 東経139.762278度 / 35.688750; 139.762278座標: 北緯35度41分19.5秒 東経139度45分44.2秒 / 北緯35.688750度 東経139.762278�...

العلاقات الطاجيكستانية الموزمبيقية طاجيكستان موزمبيق طاجيكستان موزمبيق تعديل مصدري - تعديل العلاقات الطاجيكستانية الموزمبيقية هي العلاقات الثنائية التي تجمع بين طاجيكستان وموزمبيق.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرج...
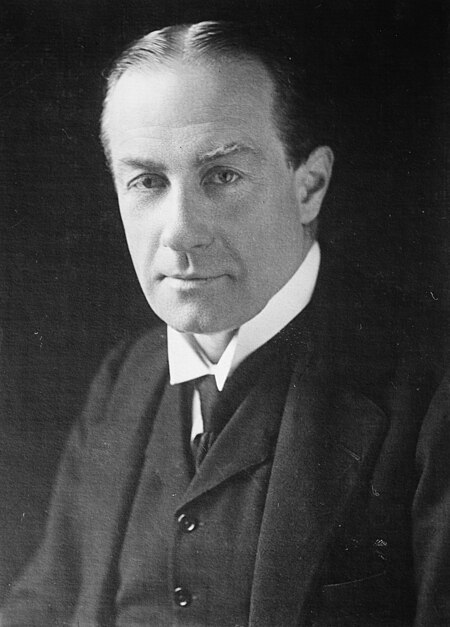
The Right HonourableThe Earl Baldwin of BewdleyKG PCBaldwin pada tahun 1920-an. Perdana Menteri Britania RayaMasa jabatan7 Juni 1935 – 28 Mei 1937Penguasa monarkiGeorge VEdward VIIIGeorge VI PendahuluRamsay MacDonaldPenggantiNeville ChamberlainMasa jabatan4 November 1924 – 5 Juni 1929Penguasa monarkiGeorge V PendahuluRamsay MacDonaldPenggantiRamsay MacDonaldMasa jabatan23 Mei 1923 – 16 Januari 1924Penguasa monarkiGeorge V PendahuluAndrew Bonar LawPenggantiRams...

برغا شعار الإحداثيات 50°45′00″N 12°10′00″E / 50.75°N 12.166666666667°E / 50.75; 12.166666666667 [1] تقسيم إداري البلد ألمانيا[2] خصائص جغرافية المساحة 43.52 كيلومتر مربع (2017)[3] ارتفاع 229 متر عدد السكان عدد السكان 3218 (31 ديسمبر 2022)[4] الكثافة...

Argentine football club Football clubClub Atlético PolicialFull nameClub Atlético PolicialNickname(s)Poli, El Xeneize de la TabladaFounded31 March 1945; 79 years ago (1945-03-31)GroundEstadio Liga Catamarqueña, San Fernando del Valle de Catamarca, ArgentinaCapacity6,500ChairmanLuis AgüeroLeagueTorneo Argentino B2011–123rd. of Zona GWebsiteClub website Home colours Away colours Club Atlético Policial is an Argentine football club, located in San Fernando del Valle de C...

Расклад карт таро во время сеанса гадания Гадание на картах Таро — один из вариантов гадания, оккультная методика, якобы позволяющая с помощью Таро раскрыть будущие события, основываясь на сформулированных вопросах. Содержание 1 История 2 Общий подход к гаданию 3 Проц�...

Association football club in England This article uses bare URLs, which are uninformative and vulnerable to link rot. Please consider converting them to full citations to ensure the article remains verifiable and maintains a consistent citation style. Several templates and tools are available to assist in formatting, such as reFill (documentation) and Citation bot (documentation). (September 2022) (Learn how and when to remove this message) Football clubNorth ShieldsFull nameNorth Shields Foo...

Depleting a renewable resourceAtlantic cod stocks were severely overexploited in the 1970s and 1980s, leading to their abrupt collapse in 1992.[1] Overexploitation, also called overharvesting, refers to harvesting a renewable resource to the point of diminishing returns.[2] Continued overexploitation can lead to the destruction of the resource, as it will be unable to replenish. The term applies to natural resources such as water aquifers, grazing pastures and forests, wild me...

KIF17 المعرفات الأسماء المستعارة KIF17, Kif17, 5930435E01Rik, AW492270, Kif17b, mKIAA1405, KIF3X, KLP-2, OSM-3, kinesin family member 17 معرفات خارجية الوراثة المندلية البشرية عبر الإنترنت 605037 HomoloGene: 5883 GeneCards: 57576 علم الوجود الجيني الوظيفة الجزيئية • nucleotide binding• microtubule motor activity• microtubule binding• plus-end-directed microtubule motor activity• ATP b...

County in Texas, United States County in TexasFort Bend CountyCountyFort Bend County Courthouse, Richmond, November 2008 SealLocation within the U.S. state of TexasTexas's location within the U.S.Coordinates: 29°32′N 95°46′W / 29.53°N 95.77°W / 29.53; -95.77Country United StatesState TexasFounded1838Named forA blockhouse positioned in a bend of the Brazos RiverSeatRichmondLargest citySugar LandArea • Total885 sq mi (2,290 km...

Ne doit pas être confondu avec Iota latin, Iota cyrillique ou yotta. Pour les articles homonymes, voir Iota (homonymie). Cette page contient des caractères spéciaux ou non latins. S’ils s’affichent mal (▯, ?, etc.), consultez la page d’aide Unicode. Iota Versions modernes de la lettre grecque iota en capitale et bas-de-casse, avec la police Times New Roman. Graphies Capitale Ι Bas de casse ι Utilisation Alphabets Grec Ordre 9e lettre Phonèmes principaux Grec anci...

ميت محسن - قرية مصرية - تقسيم إداري البلد مصر المحافظة محافظة الدقهلية المركز ميت غمر المسؤولون السكان التعداد السكاني 16381 نسمة (إحصاء 2006) معلومات أخرى التوقيت ت ع م+02:00 تعديل مصدري - تعديل قرية ميت محسن هي إحدى القرى التابعة لمركز ميت غمر في محافظة الدق...

British organisation advocating unilateral nuclear disarmament CND redirects here. For other uses, see CND (disambiguation). Campaign for Nuclear DisarmamentThe CND symbol, designed by Gerald Holtom in 1958. It has become a nearly universal peace symbol used in many different versions worldwide.[1]AbbreviationCNDFormationNovember 1957; 66 years ago (1957-11)LocationUnited KingdomRegion served United KingdomGeneral SecretaryKate HudsonChairTom UnterrainerVice-Cha...

German theologian and dissident anti-Nazi (1906–1945) Bonhoeffer redirects here. For the film, see Bonhoeffer (film). The ReverendDietrich BonhoefferBorn(1906-02-04)4 February 1906Breslau, Silesia, Prussia, Germany(now Wrocław, Poland)Died9 April 1945(1945-04-09) (aged 39)Flossenbürg, Bavaria, GermanyCause of deathExecution by hangingEducationStaatsexamen (Tübingen), Doctor of Theology (Berlin), Privatdozent (Berlin)Alma materUniversity of Tübingen University of BerlinPar...

President of Zimbabwe since 2017 Emmerson MnangagwaOfficial portrait, 20173rd President of ZimbabweIncumbentAssumed office 24 November 2017Vice PresidentConstantino ChiwengaKembo MohadiPreceded byRobert MugabePresident and First Secretary of ZANU-PFIncumbentAssumed office 19 November 2017Preceded byRobert MugabeFirst Vice-President of ZimbabweIn office12 December 2014 – 6 November 2017PresidentRobert MugabePreceded byJoice MujuruSucceeded byConstantino ChiwengaMinister ...

Election in Nevada Main article: 1872 United States presidential election 1872 United States presidential election in Nevada ← 1868 November 5, 1872 1876 → Nominee Ulysses S. Grant Horace Greeley Party Republican Liberal Republican Home state Illinois New York Running mate Henry Wilson Benjamin G. Brown Electoral vote 3 0 Popular vote 8,413 6,236 Percentage 57.43% 42.57% County Results Grant 50-60% 60-70% 70-...

U.S. cabinet member and head of the U.S. Department of Labor United States Secretary of LaborSeal of the departmentFlag of the secretaryIncumbentJulie SuActing since March 11, 2023United States Department of LaborStyleMadam Secretary (informal)The Honorable (formal)Member ofCabinetReports toPresident of the United StatesSeatFrances Perkins Building, Washington, D.C.AppointerThe President of the United Stateswith Senate advice and consentTerm lengthNo fixed termConstituting instrumen...

John L. SullivanSullivan pada 1882StatistikNama asliJohn Lawrence SullivanNama panggilanBoston Strong BoyTinggi5 ft 10+1⁄2 in (1,79 m)Mencapai74 in (188 cm)KebangsaanAmerika SerikatLahir(1858-10-15)15 Oktober 1858Roxbury, Massachusetts, ASMeninggal2 Februari 1918(1918-02-02) (umur 59)Abington, Massachusetts, ASCatatan tinjuTotal perkelahian44Menang40Menang oleh KO34Kalah1Imbang2Tanpa kontes1 John Lawrence Sullivan (15 Oktober 1858 – 2 Februa...







