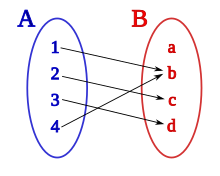
Ensemble de définition
|
Read other articles:

Detsl [1]Informasi latar belakangNama lahirKirill Aleksandrovich TolmatskyNama lainLe Truk, Giuseppe ZhyostkoLahir(1983-07-22)22 Juli 1983AsalMoskwa, RusiaMeninggal3 Februari 2019(2019-02-03) (umur 35)Izhevsk, RusiaGenreHip hop Rusia, reggae, raggaArtis terkaitBad Balance, Timati Kirill Aleksandrovich Tolmatsky (Rusia: Кири́лл Алекса́ндрович Толмацкийcode: ru is deprecated ; 22 Juli 1983 – 3 Februari 2019)[2] atau yang lebih d...

سفارة جنوب أفريقيا في السويد جنوب أفريقيا السويد الإحداثيات 59°20′01″N 18°02′41″E / 59.33361111°N 18.04472222°E / 59.33361111; 18.04472222 البلد السويد المكان ستوكهولم الاختصاص السويد، ولاتفيا[1]، وليتوانيا[2] الموقع الالكتروني الموقع الرسمي تعديل مصدري - تعديل ...

Berikut ini adalah daftar merek milik Unilever, perusahaan multinasional asal Britania yang menjual barang kebutuhan sehari-hari. Merek-merek bernilai miliaran euro Gudang dengan logo AXE, Dove, Rexona, Viss, Domestos, Coral Merek-merek di bawah ini memiliki penjualan tahunan satu miliar euro atau lebih:[1] Axe/Lynx Dove Omo/Persil Es krim Wall's (Heartbrand) Hellmann's Knorr Lipton Lux Magnum Rexona/Degree Lifebuoy Sunsilk Sunlight Makanan dan minuman Bumbu dan ekstrak Amora – mayo...

artikel mungkin mengandung informasi sangat rinci yang menarik perhatian pembaca tertentu saja. Bantu kami dengan memecah atau memindahkan informasi relevan apapun dan menghapus informasi berlebihan yang bertentangan dengan kebijakan Wikipedia. (Pelajari cara dan kapan saatnya untuk menghapus pesan templat ini) Fakultas KedokteranRumpun Ilmu KesehatanUniversitas IndonesiaSignature FK UI [1]MotoMedical Education and Research Excellent for Humanity[2]Moto dalam bahasa Indon...

Fibre en cours de séchage après rouissage. Corde de Jute. La fibre de jute, aussi appelée le jute[1], est obtenue de l'écorce du jute et est principalement produite en Inde et au Bangladesh. Elle est longue, douce et brillante et est entre autres utilisée pour faire des sacs en toile de jute ou encore comme géotextile[2]. La fibre de jute est extraite des tiges de Corchorus capsularis et de Corchorus olitorius. Le mot jute a deux acceptions :1) plante herbacée exotique du genre Co...

Kailash dan Kailasa dialihkan ke halaman ini. Untuk penggunaan lain, lihat Kailash (disambiguasi) dan Kailasa (grup musik). Mount Kailashགངས་རིན་པོ་ཆེGunung Kailash dari selatanTitik tertinggiKetinggian6.638 m (21.778 ft)Puncak1.319 m (4.327 ft)Koordinat31°4′0″N 81°18′45″E / 31.06667°N 81.31250°E / 31.06667; 81.31250Koordinat: 31°4′0″N 81°18′45″E / 31.06667°N 81.31250°E / 31.0...

Government agency Public Prosecution Service of CanadaService des poursuites pénales du CanadaAgency overviewFormed2006 (2006)PrecedingFederal Prosecution ServiceJurisdictionCanadaHeadquarters160 Elgin Street – 12th Floor, Ottawa, Ontario, K1A 0H8Employees1040170 private-sector law firms432 individually appointed lawyersAnnual budget$201,300,000 (2018–19)[1]Minister responsibleHon. Arif Virani, Attorney General of CanadaAgency executiveKathleen Roussel, Director of Public Pr...

Artikel atau sebagian dari artikel ini mungkin diterjemahkan dari Louis Antoine de Bougainville di en.wikipedia.org. Isinya masih belum akurat, karena bagian yang diterjemahkan masih perlu diperhalus dan disempurnakan. Jika Anda menguasai bahasa aslinya, harap pertimbangkan untuk menelusuri referensinya dan menyempurnakan terjemahan ini. Anda juga dapat ikut bergotong royong pada ProyekWiki Perbaikan Terjemahan. (Pesan ini dapat dihapus jika terjemahan dirasa sudah cukup tepat. Lihat pula: pa...

Questa voce sull'argomento calciatori guatemaltechi è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Carlos Villa Nazionalità Guatemala Calcio Ruolo Attaccante Squadra Concordia Chiajna Carriera Squadre di club1 2008-2009 Hartford Hawks34 (20)2010-2011 CSD Municipal? (?)2011-2012 Antigua GFC? (?)2012- Concordia Chiajna0 (0) Nazionale 2011- Guatemala1 (0) 1 I due numeri i...

М. Андриолли. Вождение козы в барском имении. Западная Белоруссия, XIX век Украинские персонажи обряда. 1926 год Вождение козы (хождение с козой, польск. Chodzenie z kozą[1]) славянский обряд вождения ряженого козой, исполняемый на Святки (чаще в Щедрый вечер) или на Масленицу (Мяс�...

Association football club Football clubBrighouse TownFull nameBrighouse Town Football ClubNickname(s)TownFounded1963GroundSt Giles Road, BrighouseCapacity1,000 (100 seated)[1]ChairmanChris ListerManagerPaul Quinn (Interim)LeagueNorthern Premier League Division One East2023–24Northern Premier League Division One East, 19th of 20 (relegated) Home colours Away colours Brighouse Town Football Club is a football club based in Brighouse, West Yorkshire, England. They are currently members...

It has been suggested that this article be merged into Boston cream pie. (Discuss) Proposed since March 2024. Cream-filled American doughnut Boston cream doughnutAlternative namesBoston cream pie doughnutBoston cream pie donutTypeDoughnutPlace of originBostonRegion or stateNew EnglandMain ingredientsDough, chocolate icing, custard Media: Boston cream doughnut The Boston cream doughnut (or Boston cream pie doughnut, also spelled donut, or simply Boston Cream) is a round, solid, yeast...

土库曼斯坦总统土库曼斯坦国徽土库曼斯坦总统旗現任谢尔达尔·别尔德穆哈梅多夫自2022年3月19日官邸阿什哈巴德总统府(Oguzkhan Presidential Palace)機關所在地阿什哈巴德任命者直接选举任期7年,可连选连任首任萨帕尔穆拉特·尼亚佐夫设立1991年10月27日 土库曼斯坦土库曼斯坦政府与政治 国家政府 土库曼斯坦宪法 国旗 国徽 国歌 立法機關(英语:National Council of Turkmenistan) ...

Japanese manga series Hen na Chishiki ni Kuwashii Kanojo Takayukashiki Sōko-sanFirst tankōbon volume cover変な知識に詳しい彼女 高床式草子さんGenreRomantic comedy[1] MangaWritten byOhanachanPublished byKodanshaMagazineWeekly Young MagazineDemographicSeinenOriginal runJanuary 22, 2018 – March 9, 2020Volumes5 Hen na Chishiki ni Kuwashii Kanojo Takayukashiki Sōko-san (変な知識に詳しい彼女 高床式草子さん) is a Japanese manga series written a...

淡江高峰塔倒塌事件高峰塔B座、C座公寓,與倒塌的A座公寓結構類似 (2012)日期1993年12月11日,30年前(1993-12-11)时间下午1时35分(马来西亚标准时间,周六)地点 马来西亚雪兰莪淡江(英语:Ulu Klang)山景花园(英语:Taman Hillview)高峰塔坐标3°10′33.4″N 101°45′42.1″E / 3.175944°N 101.761694°E / 3.175944; 101.761694坐标:3°10′33.4″N 101°45′42.1″E&...

Tram museum in Ballarat, Victoria This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article relies excessively on references to primary sources. Please improve this article by adding secondary or tertiary sources. Find sources: Ballarat Tramway Museum – news · newspapers · books · scholar · JSTOR (June 2020) (Learn how and when to remove this me...

Possible truths which are not necessary In logic, contingency is the feature of a statement making it neither necessary nor impossible.[1][2] Contingency is a fundamental concept of modal logic. Modal logic concerns the manner, or mode, in which statements are true. Contingency is one of three basic modes alongside necessity and possibility. In modal logic, a contingent statement stands in the modal realm between what is necessary and what is impossible, never crossing into th...

Al-Mas'udi immaginato dallo scultore austriaco Emmerich Alexius Swoboda con una statua affacciata sul lato destro della Bellariastraße, sul tetto del Museo di storia naturale di Vienna. Abū al-Ḥasan ʿAlī al-Masʿūdī (Baghdad, 897 – al-Fustat, 957) è stato uno storico, geografo e viaggiatore arabo. Indice 1 Biografia 2 Opere 3 Note 4 Bibliografia 5 Altri progetti 6 Collegamenti esterni Biografia Abū al-Ḥasan ʿAlī al-Masʿūdī (in arabo ﺍﺑﻮ ﺍﻟﺤﺴﻦ ﻋﻠﻲ ...

Village in Southern Transdanubia, HungarySzentbalázsVillageView of Szentbalázs Coat of armsLocation of Somogy county in HungarySzentbalázsLocation of SzentbalázsCoordinates: 46°19′16″N 17°53′49″E / 46.32105°N 17.89682°E / 46.32105; 17.89682Country HungaryRegionSouthern TransdanubiaCountySomogyDistrictKaposvárRC DioceseKaposvárArea • Total12.14 km2 (4.69 sq mi)Population (2017) • Total294[1]Demon...

Relation between sides and angles of a triangle Figure 1 – A triangle. The angles α, β, and γ are respectively opposite the sides a, b, and c. Trigonometry Outline History Usage Functions (sin, cos, tan, inverse) Generalized trigonometry Reference Identities Exact constants Tables Unit circle Laws and theorems Sines Cosines Tangents Cotangents Pythagorean theorem Calculus Trigonometric substitution Integrals (inverse functions) Derivatives Trigonometric series Mathematicia...






![{\displaystyle D_{g}=\;]0,+\infty [}](https://wikimedia.org/api/rest_v1/media/math/render/svg/157f4184f5b7d2003063a11a12e5abe7ff4e2ce5)






