Décomposition de Bruhat
|
Read other articles:

Cet article est une ébauche concernant le Concours Eurovision de la chanson et l’Arménie. Vous pouvez partager vos connaissances en l’améliorant (comment ?) ; pour plus d’indications, visitez le projet Eurovision. Arménieau Concours Eurovision 2010 Données clés Pays Arménie Chanson Apricot Stone Interprète Eva Rivas Compositeur Armen Martirosyan Parolier Karen Kavaleryan Langue Anglais Sélection nationale Type de sélection jury + télévote Date 14 février 20...

Hong Kong padaOlimpiade Musim Dingin 2010Kode IOCHKGKONFederasi Olahraga dan Komite Olimpiade Hong Kong, TiongkokSitus webwww.hkolympic.org (dalam bahasa Mandarin)Penampilan pada Olimpiade Musim Dingin 2010 di VancouverPeserta1 dalam 1 cabang olahragaPembawa benderaHan YueshuangMedali 0 0 0 Total 0 Penampilan pada Olimpiade Musim Dingin (ringkasan)200220062010201420182022 Hong Kong ikut serta dalam Olimpiade Musim Dingin 2010 di Vancouver, British Columbia, Kanada. Atlet H...

Artikel ini bukan mengenai Bidang vektor. Halaman ini berisi artikel tentang ruang linear (vektor). Untuk struktur dalam geometri kejadian, lihat Ruang linear (geometri). Untuk perusahaan teknologi ruang, lihat Sistem Ruang Vektor. Penjumlahan vektor dan perkalian skalar: Sebuah vektor v (biru) ditambahkan ke vektor lain w (merah, ilustrasi atas). Di bawah, w diregangkan dengan faktor 2, menghasilkan jumlah v + 2·w. Ruang vektor adalah struktur matematika yang dibentuk oleh sekumpulan vektor...

Japans herrlandslag i ishockeyIIHF:s rankning21 (2014)Coach Mark MahonGuld-Silver-Brons-OS-meriterGuld-Silver-Brons-Canada/World Cup-meriterGuld-Brons- Japans herrlandslag i ishockey representerar Japan i ishockey för herrar. Första matchen spelades den 24 januari 1930 i Prag, och förlorades med 2-13 mot det dåvarande Tjeckoslovakien [1]. Då orten Nagano i Japan arrangerade Olympiska vinterspelen 1998 deltog Japan i OS-ishockeyturneringen som direktkvalificerat hemmalag, och slutade på ...

Artificial island near Montreal, Quebec, Canada Notre-Dame IslandNotre-Dame IslandSite by Montreal Island, in St. Lawrence RiverGeographyLocationSaint Lawrence RiverCoordinates45°30′15″N 73°31′35″W / 45.50417°N 73.52639°W / 45.50417; -73.52639AdministrationCanadaProvinceQuebecCityMontrealBoroughVille-MarieDemographicsPopulation0 Notre Dame Island (French: Île Notre-Dame) is an artificial island in the Saint Lawrence River in Montreal, Quebec, Canada. It is...

Синелобый амазон Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:ЗавропсидыКласс:Пт�...

Part of the series onHistory of Montreal History Hochelaga (village)(16th century)Old Montreal(since 17th century)North West Company(1779–1821)Merger and demerger(2001–2005) Timeline of Montreal history Founded by Maisonneuve 1642Sulpicians takeover 1663Great Peace of Montreal 1701British takeover 1760Lachine Canal opened 1825Burning of the Parliament 1849Universal and Int'l Exhibition 1967October Crisis 1970Summer Olympics 1976 Other Oldest buildings National Historic Sites List of gove...

2016年美國總統選舉 ← 2012 2016年11月8日 2020 → 538個選舉人團席位獲勝需270票民意調查投票率55.7%[1][2] ▲ 0.8 % 获提名人 唐納·川普 希拉莉·克林頓 政党 共和黨 民主党 家鄉州 紐約州 紐約州 竞选搭档 迈克·彭斯 蒂姆·凱恩 选举人票 304[3][4][註 1] 227[5] 胜出州/省 30 + 緬-2 20 + DC 民選得票 62,984,828[6] 65,853,514[6]...

Bendungan Cipanas. Bendungan Cipanas terletak di kabupaten Sumedang, Jawa Barat. Bendungan Cipanas ini merupakan sebuah bendungan multifungsi yang tepatnya berada di Desa Cibuluh, Kecamatan Ujungjaya, Kabupaten Sumedang, Provinsi Jawa Barat. Sumber air bendungan Cipanas berasal dari sungai Cipanas yang merupakan bagian dari wilayah Sungai Cimanuk-Cisanggarung, dan memiliki tipe tanah urugan inti tegak yang dibangun dengan tinggi 71,60 meter dan dilengkapi dengan terowongan pengelak sepanjang ...

Religion in Madagascar A mosque in Antananarivo. Ethnicity of Madagascan Muslims (2021 estimate)[1] Malagasy (65%) Comorians, Indians, Pakistanis, and others (35%) Islam by countryWorld percentage of Muslims by country Africa Algeria Angola Benin Botswana Burkina Faso Burundi Cameroon Cape Verde Central African Republic Chad Comoros Democratic Republic of the Congo Republic of the Congo Djibouti Egypt Equatorial Guinea Eritrea Eswatini Ethiopia Gabon Gambia Ghan...

Herbert KroemerKroemer pada 2008Lahir(1928-08-25)25 Agustus 1928Weimar, Thuringia, JermanMeninggal8 Maret 2024(2024-03-08) (umur 95)KebangsaanJermanAmerika SerikatAlmamaterUniversitas JenaUniversitas GöttingenDikenal atasTransistor medan driftHeterostruktur ganda laserTransistor bipolar heterojungsiPenghargaanPenghargaan J J Ebers (1973)Penghargaan Penelitian Humboldt (1994)Penghargaan Nobel Fisika (2000)IEEE Medal of Honor[1](2002)Karier ilmiahBidangTeknik Elektro, Fisika Tera...
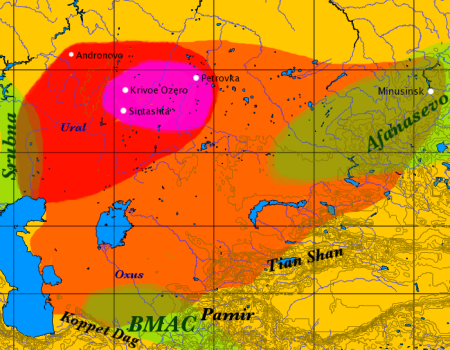
Archeological site in Chelyabinsk Oblast, Russia SintashtaСинташта́Location of the Sintashta culture (violet)Shown within Continental AsiaShow map of Continental AsiaSintashta (Russia)Show map of RussiaLocationChelyabinsk Oblast, RussiaCoordinates52°29′10.4″N 60°11′17.8″E / 52.486222°N 60.188278°E / 52.486222; 60.188278TypeSettlement Sintashta[a] is an archaeological site in Chelyabinsk Oblast, Russia. It is the remains of a fortified settl...

القديس جورج (جامعة لندن) معلومات التأسيس 1733 الموقع الجغرافي إحداثيات 51°25′37″N 0°10′29″W / 51.426944444444°N 0.17472222222222°W / 51.426944444444; -0.17472222222222 المدينة توتينغ [لغات أخرى]، ولندن[1] الرمز البريدي SW17 0RE[1] المكان واندزورث البلد المملكة المت...

Stasiun Ikebukuro池袋駅Gedung Stasiun Ikebukuro (sisi timur) pada malam hari, menghadap selatan di Meiji-Dori.LokasiPrefekturTokyo(Lihat stasiun lainnya di Tokyo)Distrik kotaToshimaAlamat1-chome, Minami-Ikebukuro (JR, Seibu)Alamat dalam bahasa Jepang東京都豊島区南池袋一丁目SejarahDibuka1903Layanan kereta apiOperatorJR East, Seibu Railway, Tōbu Railway, Tokyo MetroJalurJalur YamanoteJalur SaikyōJalur Shōnan-ShinjukuJalur Ikebukuro SeibuJalur Tōjō TōbuJalur MarunouchiJalur ...

Papusza Wajs Bronislawa Wajs dite Papusza Données clés Nom de naissance Bronislawa Wajs Naissance 17 août 1908 Lublin ou Plonsk Décès 8 février 1987 (à 78 ans) Inowrocław Activité principale Poète, chanteuse, musicienne, diseuse de bonne aventure Auteur Langue d’écriture rromani, polonais Mouvement Inclassable Genres Poésie Œuvres principales Piesny Papuszy, Wroclaw, Ossolineum, 1956; Piesni Mowione, Lodz, 1973. modifier Bronisława Wajs, dite Papusza (Lublin?, 17 août 1...

Cet article est une ébauche concernant le Concours Eurovision de la chanson et l’Albanie. Vous pouvez partager vos connaissances en l’améliorant (comment ?) ; pour plus d’indications, visitez le projet Eurovision. Albanieau Concours Eurovision 2009 Données clés Pays Albanie Chanson Carry Me in Your Dreams Interprète Kejsi Tola Compositeur Edmond Zhulali Parolier Agim Doçi Langue Anglais Sélection nationale Type de sélection Émission téléviséeChoix par 7 jur�...

Federasi Sepak Bola NorwegiaUEFADidirikan1902Kantor pusatOsloBergabung dengan FIFA1908Bergabung dengan UEFA1954PresidenLise KlavenessWebsitewww.fotball.no Federasi Sepak Bola Norwegia (bahasa Norwegia: Norges Fotballforbund (NFF)) adalah badan pengendali sepak bola di Norwegia. Kompetisi Badan ini menyelenggarakan beberapa kompetisi di Norwegia, yakni: Liga Utama Norwegia Liga Divisi Satu Norwegia Liga Divisi Dua Norwegia Piala Sepak Bola Norwegia Piala Super Norwegia Tim nasional Badan i...

American writer and television producer Rift FournierRift Fournier, St. Louis 2013Born(1936-05-16)May 16, 1936Wichita, KansasDiedOctober 6, 2013(2013-10-06) (aged 77)St. Louis, MissouriOccupation(s)Screenwriter, producer Rift Fournier (May 16, 1936 – October 6, 2013) was an American writer, screenwriter and television producer. Fournier, who lost the ability to walk at 17 years old due to polio, had a long and diverse career in television.[1][2] He wrote episodes of num...

足跡中心Footprint CenterThe Purple PalaceThe Snake Pit球館北側出入口 (攝於2015年)曾用名美西航空球館(1992–2006)全美航空中心(2006–2015)托金斯迪克度假酒店球館(2015–2020)鳳凰城太陽球館(2020-2021)足跡中心(2021-)位置 美国亞利桑那州鳳凰城公共交通 第3街/傑斐遜與第3街/華盛頓站所有者鳳凰城營運者Phoenix Arena Development, L.P.座位数18,422[2]建造動工1990年8月1日 (...

David Óistraj (izquierda) con Franz Konwitschny (centro) e Ígor Óistraj (derecha), en 1957. David Fiódorovich Óistraj (en ruso: Дави́д Фё́дорович О́йстрах) (Odesa, 30 de septiembre de 1908 - Ámsterdam, 24 de octubre de 1974) fue un violinista soviético, uno de los de mayor prestigio del siglo XX. Biografía Los primeros años Nació en la cosmopolita Odesa, junto al mar Negro, en aquel momento parte de la Rusia zarista (ahora Ucrania), en la modesta familia...


