Combinatoire topologique
|
Read other articles:

Peta wilayah Vecoux. Vecoux merupakan sebuah komune di departemen Vosges yang terletak pada sebelah timur laut Prancis. Lihat pula Komune di departemen Vosges Referensi INSEE lbsKomune di departemen Vosges Les Ableuvenettes Ahéville Aingeville Ainvelle Allarmont Ambacourt Ameuvelle Anglemont Anould Aouze Arches Archettes Aroffe Arrentès-de-Corcieux Attignéville Attigny Aulnois Aumontzey Autigny-la-Tour Autreville Autrey Auzainvilliers Avillers Avrainville Avranville Aydoilles Badménil-aux...

Danil IshutinDendiStatusAktifTanggal lahir30 Desember 1989 (umur 34)Tempat tinggalLviv, UkrainaKebangsaanUkrainaTim saat iniNatus Vincere (Tidak Aktif)PermainanDefense of the Ancients Dota 2Hadiah selama karier$710.580,69Riwayat karir2010–2018Natus Vincere2019Tigers2020–presentB8 Pencapaian dan penghargaan Pemenang The International (2011) Situs web resmi Danilo Ishutin Aleksandrovich (Ukrainian: Ішутін Данило Олександровичcode: uk is deprecated ) (lahir 30 D...

Discrimination against asexual people This article is about discrimination of people who lack sexual attraction or interest in sexual activity. For discrimination of people who do not experience romantic attraction, see Discrimination against aromantic people. The examples and perspective in this article deal primarily with the United States and the United Kingdom and do not represent a worldwide view of the subject. You may improve this article, discuss the issue on the talk page, or create ...

Schwenk crew on duty Schwenker-tripod from the smithy Schwenker (German: [ˈʃvɛŋkɐ] ⓘ) is a local term from the German state of Saarland, the Mosel Valley and big parts of Rheinland Pfalz and is used in three ways, all relating to the same grilled meat:[1] Schwenker or Schwenkbraten is a marinated pork neck steak which originates from the Saarland (known there as Schwenksteak) and is grilled on a Schwenker (2). Normally either a green herb or red paprika marinade is used...

Disambiguazione – Se stai cercando la guerra del XVI secolo, vedi Guerra di successione polacca (1587-1588). Questa voce o sezione sull'argomento conflitti non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Segui i suggerimenti del progetto di riferimento. Guerra di successione polaccaL'assedio di Danzica, tavola dipinta di un anonimo.Data1733 – 1738 Lu...

烏克蘭總理Прем'єр-міністр України烏克蘭國徽現任杰尼斯·什米加尔自2020年3月4日任命者烏克蘭總統任期總統任命首任維托爾德·福金设立1991年11月后继职位無网站www.kmu.gov.ua/control/en/(英文) 乌克兰 乌克兰政府与政治系列条目 宪法 政府 总统 弗拉基米尔·泽连斯基 總統辦公室 国家安全与国防事务委员会 总统代表(英语:Representatives of the President of Ukraine) 总...

此条目序言章节没有充分总结全文内容要点。 (2019年3月21日)请考虑扩充序言,清晰概述条目所有重點。请在条目的讨论页讨论此问题。 哈萨克斯坦總統哈薩克總統旗現任Қасым-Жомарт Кемелұлы Тоқаев卡瑟姆若马尔特·托卡耶夫自2019年3月20日在任任期7年首任努尔苏丹·纳扎尔巴耶夫设立1990年4月24日(哈薩克蘇維埃社會主義共和國總統) 哈萨克斯坦 哈萨克斯坦政府...

Raden Agus Prasetyo Utomo Irlat Itum ItjenadPetahanaMulai menjabat 17 Juli 2023PendahuluFuladPenggantiPetahana Informasi pribadiLahir4 Agustus 1971 (umur 52)Glodog, Pelem, Karangrejo, Magetan, Jawa TimurOrang tuaR. Suyono dan (ayah)Annaisyah (ibu)Alma materAkademi Militer (1995)PekerjaanMiliterKarier militerPihak IndonesiaDinas/cabang TNI Angkatan DaratMasa dinas1995—sekarangPangkat Brigadir JenderalSatuanInfanteriSunting kotak info • L • B Brigadir Jenderal...

2015 Slovenian same-sex marriage referendum 20 December 2015 Are you in favor of the Law on Amendments and Additions to the Marriage and Family Status Act, which the National Assembly adopted in the session of 3 March 2015?Results Choice Votes % Yes 226,651 36.49% No 394,482 63.51% Valid votes 621,133 99.62% Invalid or blank votes 2,356 0.38% Total votes 623,489 100.00% Registered voters/turnout 1,714,055 36.38% Results by constituenciesPolitics of Slovenia UN Member State(UNSC Member · ECO...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Quesnel Highland – news · newspapers · books · scholar · JSTOR (February 2023) (Learn how and when to remove this message) Quesnel HighlandHighlandsApproximate boundary of the Quensel HighlandCoordinates: 52°30′00″N 121°00′00″W / 52.50...

City and seaport in Marche, Italy This article is about the city in Italy. For other uses, see Ancona (disambiguation). Comune in Marche, ItalyAnconaComuneCittà di AnconaClockwise from top: view of the city, Mole Vanvitelliana, Scalinata del Passetto [it] and Piazza IV Novembre with the Monument to the Fallen, Loggia dei Mercanti, San Ciriaco Cathedral, Piazza del Plebiscito (Piazza del Papa) [it], the Arch of Trajan and Arch of Clementino [it] FlagCoat...

Neighborhood in Chicago Part of a series onEthnic groups in Chicago African Americans Albanians Appalachian Belarusians Bosnians Chinese Czechs Germans Greeks Iraqi Irish Indians Italians Japanese Jews Koreans Latvians Lithuanians Luxembourgers Mexicans Native peoples Poles Puerto Ricans Roma Swedes Ukrainians Welsh vte The National Hellenic Museum in Greektown, Chicago Outside of the restaurant Greek Islands, blue pots painted with famous Greek patterns, such as the Greek key, adorn the side...

2-Ethoxyethyl acetate Names Preferred IUPAC name 2-Ethoxyethyl acetate Other names Ethyglycol acetate; Ethylene glycol mono ethyl ether acetate; 2-EEA; Ethoxyethanol acetate; EGA; Cellosolve acetate; Ethoxol acetate; Oxidol acetate Identifiers CAS Number 111-15-9 3D model (JSmol) Interactive image ChemSpider 13839109 ECHA InfoCard 100.003.491 EC Number 203-839-2 PubChem CID 8095 RTECS number KK8225000 UNII DG1O0Z7390 UN number 1172 CompTox Dashboard (EPA) DTXSID9021928 InChI InChI=1S/C6H12O3...

American statistician and computer scientist (1944–2021) Leland WilkinsonBorn(1944-11-05)November 5, 1944DiedDecember 10, 2021(2021-12-10) (aged 77)Lake Forest, Illinois, U.S.Alma mater Harvard University (A.B.) Harvard Divinity School (S.T.B.) Yale University (Ph.D.) Known forThe Grammar of GraphicsSpouses Ruth Elaine VanDemark (m. 1967; died 2012) Marilyn Vogel (m. 2013) Children2, including ...

Census division in Manitoba, Canada Location of Division 1 in Manitoba Division No. 1 is a census division located within the Eastman Region of the Canadian province of Manitoba. Unlike in some other provinces, census divisions do not reflect the organization of local government in Manitoba. These areas exist solely for the purposes of statistical analysis and presentation; they have no government of their own. It is located in the south-eastern corner of the province, lying between the Lake ...

1871–1918 empire in Central Europe This article is about the German nation-state existing from 1871 until 1918. For other uses, see German Empire (disambiguation). German EmpireDeutsches Reich (German)1871–1918 Flag Coat of arms(1889–1918)[1] Motto: Gott mit uns (German)[2]Nobiscum Deus (Latin)(God with us)Anthem: Heil dir im Siegerkranz[3](Hail to Thee in the Victor's Crown) Die Wacht am Rhein (unofficial)[4][5][6](The Watc...

Feminine figure in Gnosticism Part of a series onGnosticism Gnostic concepts Adam kasia Adam pagria Aeon Anima mundi Archon Barbelo Demiurge Five Seals Gnosis Kenoma Luminary Manda Monad Ogdoad Pleroma Sophia Uthra World of Light World of Darkness Yaldabaoth Gnostic sects and founders List of Gnostic sects Proto-Gnosticism Maghāriya Thomasines Judean / Israelite Adam Mandaeism Elksai Elkasaites Samaritan Baptist Dositheos Simon Magus (Simonians) Menander Quqites Christian Gnosticism A...
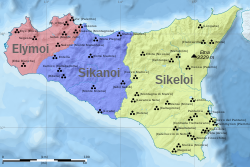
Ancient tribal people in western Sicily This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Elymians – news · newspapers · books · scholar · JSTOR (January 2022) (Learn how and when to remove this message) You can help expand this article with text translated from the corresponding article in Polish. (April...

Gaetano Arfé Senatore della Repubblica ItalianaDurata mandato1972 (VI), 1987 (X) –1976 (VI), 1992 (X) LegislaturaVI, X GruppoparlamentarePartito Socialista Italiano (VI), Sinistra Indipendente (X) CircoscrizioneEmilia Romagna CollegioParma (VI) e Rimini (X) Sito istituzionale Deputato della Repubblica ItalianaDurata mandato1976 –1979 LegislaturaVII GruppoparlamentarePartito Socialista Italiano CircoscrizioneEmilia Romagna CollegioParma Incarichi parlamentari&#...

Soviet physicist (1927–2006) Yuri DenisyukBornYuri Nikolayevich Denisyuk(1927-07-27)27 July 1927Sochi, Soviet UnionDied14 May 2006(2006-05-14) (aged 78)Saint Petersburg, RussiaNationalityRussianAlma materSPbNRU ITMOKnown forcreator of 3D holography, Denisyuk's SchemeAwardsLenin Prize (1970), International Film Organization Prize “Intercamera” (1971), The Order of the Badge of Honour (1975), USSR State Prize (1982, 1989), The International Dennis Gabor Award (1983), Great ...






