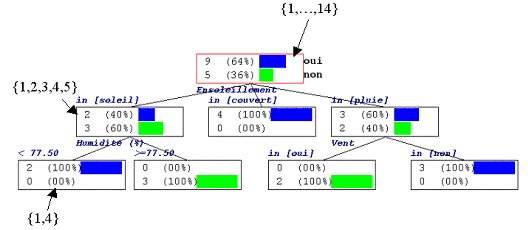
Arbre de décision
|
Read other articles:

Neith-hotep/Hotep-Neith Era: Kerajaan Baru(1550–1069 BC) Hieroglif Mesir Fragmen Alabaster dengan nama ratu Neith-hotep Neithhotep atau Neith-hotep merupakan seorang Permaisuri Mesir Kuno yang hidup dan bertakhta selama awal Dinasti ke-1. Ia pernah dianggap sebagai penguasa laki-laki: Mastabanya yang luar biasa besarnya dan Serekh kerajaan yang mengandung namanya di beberapa jejak segel sebelumnya menyebabkan para Egiptolog dan sejarawan keliru bahwa ia mungkin seorang raja yang tidak...

Celurut pigmi Mesir Crocidura religiosa Status konservasiKekurangan dataIUCN5616 TaksonomiKerajaanAnimaliaFilumChordataKelasMammaliaOrdoEulipotyphlaFamiliSoricidaeGenusCrociduraSpesiesCrocidura religiosa Geoffroy, 1827 DistribusiPersebaran celurut pigmi Mesir lbs Celurut pigmi Mesir atau celurut keramat[1] (Crocidura religiosa) adalah sebuah spesies mamalia dalam keluarga Soricidae. Spesies tersebut adalah endemik di Mesir. Habitat alaminya adalah lahan subur. Spesies tersebut teranca...

Cahill ministry57th Cabinet of the State of New South WalesPremier Joe CahillDate formed15 March 1956Date dissolved1 April 1959People and organisationsMonarchElizabeth IIGovernorSir John NorthcottSir Eric WoodwardPremierJoe CahillDeputy PremierBob HeffronNo. of ministers15Member partyLaborStatus in legislatureMajority governmentOpposition partyLiberal/Country coalitionOpposition leaderPat MortonHistoryElection(s)1956 New South Wales electionPredecessorSecond Cahill ministrySuccessorFourth Ca...

Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber: Elba – berita · surat kabar · buku · cendekiawan · JSTOR Untuk kegunaan lain, lihat Elba (disambiguasi). Pulau ElbaNama lokal: Isola d'ElbaPemandangan pantai Portoferraio di Pulau ElbaGeografiLokasiLaut ...

Neighborhood of Beverly, Massachusetts, US Neighborhood of Beverly in Essex, Massachusetts, United StatesBeverly FarmsNeighborhood of BeverlyBeverly Farms Fire Station on the 4th of July in 2006.Nickname: FarmsMotto(s): Filled with History and TraditionCountryUnited StatesStateMassachusettsCountyEssexNeighborhood ofBeverlyPopulation7,929Time zoneUTC-5 (Eastern)Zip Code01915Area code351 / 978 Beverly Farms is a neighborhood comprising the eastern part of the city of Beverly, Massachu...

Place in Sindh, PakistanSanghar District ضلع سانگھڑسانگهڙ ضلعوTop: Mosque at ShahdadpurBottom: Fields near SirhinwariSanghar is located in the centre of Sindh.Country PakistanProvince SindhDivisionShaheed Benazir AbadSeatSangharGovernment • TypeDistrict Administration • MNA SangharShazia Janat MariArea • Total10,728 km2 (4,142 sq mi)Population (2017)[1] • Total249,873 • ...

Supreme Court of the United States38°53′26″N 77°00′16″W / 38.89056°N 77.00444°W / 38.89056; -77.00444EstablishedMarch 4, 1789; 235 years ago (1789-03-04)LocationWashington, D.C.Coordinates38°53′26″N 77°00′16″W / 38.89056°N 77.00444°W / 38.89056; -77.00444Composition methodPresidential nomination with Senate confirmationAuthorized byConstitution of the United States, Art. III, § 1Judge term lengthl...

مبنى البنك المركزي الأوروبي في فرانكفورت-ألمانيا توسيع منطقة اليورو هو عملية مستمرة داخل الاتحاد الأوروبي. تلتزم كافة الدول الأعضاء في الاتحاد الأوروبي، باستثناء الدنمارك التي تفاوضت على الانسحاب من الأحكام، بتبنّي اليورو باعتباره العملة الوحيدة في البلاد بعد أن تحقق ت�...

Canadian ice hockey player, coach, and scout Ice hockey player Craig Hartsburg Born (1959-06-29) June 29, 1959 (age 64)Stratford, Ontario, CanadaHeight 6 ft 1 in (185 cm)Weight 200 lb (91 kg; 14 st 4 lb)Position DefenceShot LeftPlayed for Birmingham BullsMinnesota North StarsNational team CanadaNHL Draft 6th overall, 1979Minnesota North StarsPlaying career 1978–1989 Craig William Hartsburg (born June 29, 1959) is a Canadian former profession...

Si ce bandeau n'est plus pertinent, retirez-le. Cliquez ici pour en savoir plus. La mise en forme de cet article est à améliorer (février 2021). La mise en forme du texte ne suit pas les recommandations de Wikipédia : il faut le « wikifier ». Cet article est une ébauche concernant l’alimentation, la politique et l’économie. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Récolte du ma�...

Painting by Raphael Madonna with the FishArtistRaphaelYearc. 1512–1514Typeoil on boardDimensions113 cm × 88 cm (44 in × 35 in)LocationMuseo del Prado, Madrid Madonna of the Fish, known also as Madonna with the Fish is a painting by the High Renaissance master Raphael, dated to 1512-14. It is now in the Museo del Prado, Madrid. Mary sits enthroned with Jesus on her knee. On one side is St. Jerome kneeling by the Lion; he is holding a book. On the o...

American politician (1885–1940) Roy Alvin BaldwinBaldwin in 1923Member of the Texas House of Representatives from the 122nd districtIn officeMay 20, 1920 – January 9, 1923Preceded byWilliam H. BledsoeSucceeded byDewey YoungMember of the Texas House of Representatives from the 119th districtIn officeJanuary 9, 1923 – January 13, 1925Preceded byJohn QuaidSucceeded byJames K. Wester Personal detailsBorn(1885-01-02)January 2, 1885Mercer County, Missouri, U.S.DiedOctober 2,...

Refrancorecomune LocalizzazioneStato Italia Regione Piemonte Provincia Asti AmministrazioneSindacoRoberta Volpato (lista civica Insieme) dal 27-5-2019 TerritorioCoordinate44°56′14″N 8°20′31″E / 44.937222°N 8.341944°E44.937222; 8.341944 (Refrancore)Coordinate: 44°56′14″N 8°20′31″E / 44.937222°N 8.341944°E44.937222; 8.341944 (Refrancore) Altitudine150 m s.l.m. Superficie13,21 km² Abitanti1 551...

الهيئة السعودية للمهندسين الاختصار SCE البلد السعودية المقر الرئيسي الرياض، السعودية تاريخ التأسيس 18 نوفمبر 2002 النوع هيئة مهنية علمية الاهتمامات العلوم الهندسية منطقة الخدمة السعودية العضوية الاتحاد العالمي للمنظمات الهندسية[1] رئيس مجلس الادارة ماجد ب�...

Joe Kelly al Wondercon di Anaheim del 2012 Joseph Paul Kelly, meglio noto come Joe Kelly (1º settembre 1971), è un fumettista, scrittore e produttore televisivo statunitense. Celebre soprattutto per il suo lavoro su Deadpool per la Marvel Comics, del quale scrisse le storie dal 1997 al 1999, trasformandolo da stereotipo del personaggio action e violento anni '90 (come voleva la precedente caratterizzazione del personaggio ad opera dei suoi creatori, Rob Liefeld e Fabian Nicieza)[1] ...

Нейтральність цієї статті під сумнівом. Будь ласка, ознайомтеся з відповідним обговоренням та за можливості виправте недоліки. Запит «ДНР» перенаправляє сюди; див. також ДНР (значення). «Донецька народна республіка»рос. «Донецкая народная республика» Участь у війнах: В�...

Irene CaraLahirIrene Cara Escalera(1959-03-18)18 Maret 1959Kota New York, A.S.Meninggal25 November 2022(2022-11-25) (umur 63)Largo, Florida, A.S.PendidikanProfessional Children's SchoolPekerjaan Penyanyi penulis lagu pemeran Dikenal atasSparkle Williams – Sparkle[1] Coco Hernandez – FameSuami/istriConrad Palmisano (m. 1986; bercerai 1991)Karier musikGenreR&BpopdiscoInstrumenVokalkeyboardTahun aktif1967–2018LabelEpicGe...

Dewan Perwakilan Rakyat DaerahKabupaten TabalongDewan Perwakilan RakyatKabupaten Tabalong2019-2024JenisJenisUnikameral Jangka waktu5 tahunSejarahSesi baru dimulai12 Agustus 2019PimpinanKetuaH. Mustafa (Gerindra) sejak 25 September 2019 Wakil Ketua IH. Jurni, S.E. (Golkar) sejak 25 September 2019 Wakil Ketua IIHabib Muhammad Taufani Al Kaf, S.Kom. (PAN) sejak 25 September 2019 KomposisiAnggota30Partai & kursi PDI-P (3) NasDem (2) PKB (2) ...

Katedral Bourges Bourges merupakan nama kota di Prancis. Letaknya di bagian tengah. Tepatnya di region Centre, Prancis. Pada tahun 2005, kota ini memiliki jumlah penduduk sebanyak 69.900 jiwa dengan memiliki luas wilayah 68,74 km². Kota ini memiliki kepadatan penduduk sebanyak 1.054 jiwa/km². Pranala luar Wikimedia Commons memiliki media mengenai Bourges. Situs resmi lbsKomune di departemen Cher Achères Ainay-le-Vieil Les Aix-d'Angillon Allogny Allouis Annoix Apremont-sur-Allier Arça...

English squash player Lee BeachillLee Beachill with his 2005 US Open trophyFull nameLee BeachillCountry EnglandResidencePontefract, EnglandBorn (1977-11-28) 28 November 1977 (age 46)Huddersfield, EnglandHeight1.82 m (6 ft 0 in)Weight76 kg (168 lb)Turned Pro1998Retired2009PlaysRight HandedCoached byMalcolm WillstropRacquet usedDunlopMen's singlesHighest rankingNo. 1 (October 2004)Title(s)8Tour final(s)13World OpenF (2004) Medal r...