Arbre (mathématiques)
|
Read other articles:

CoogieInformasi latar belakangNama lahirKim Jeong-hunLahir23 Januari 1994 (umur 30)Daejeon, Korea SelatanGenreHip hopPekerjaanPenyanyi rappenulis laguTahun aktif2018-sekarangLabelAOMG Kim Jeong-hun (Hangul: 김정훈; lahir 23 Januari 1994), secara profesional dikenal sebagai Coogie (Hangul: 쿠기), adalah penyanyi rap dan penulis lagu Korea Selatan. Ia memperoleh popularitas ketika tampil di Show Me The Money 777 pada tahun 2018. Ia menandatagani kontrak dengan label ...

Lale Andersen di tamannya pada tahun 1952, di Zollikon Lale Andersen (23 Maret 1905 – 29 Agustus 1972) adalah penulis musik-lagu chanson Jerman[note a] lahir di Bremerhaven, Jerman. Dia menjadi terkenal setelah lagu ciptaanya berjudul Lili Marleen pada 1939, menjadi populer sejak era Perang Dunia II. Kehidupan awal Dia lahir di Lehe, sekarang Bremerhaven[note b] dan memiliki nama baptis Elisabeth Carlotta Helena Berta Bunnenberg[1] Pada 1922, di usia 17 tahun[note c], dia menikah de...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada November 2022. Al-Harits V bin JabalahRaja Ghassaniyah, Patrisius Romawi, dan Filarkhos SarakenBerkuasak. 528 – 569 MPendahuluJabalah IVPenerusal-Mundzir IIIKematian569AyahJabalah IV Al-Ḥarits bin Jabalah (Arab: الحارث بن جبلةcode: ar is deprecated )...

Albert HalimLahirAlbert Halimin17 September 1986 (umur 37)Jakarta, IndonesiaPekerjaanAktorTahun aktif2011—sekarang Albert Halimin (lahir 17 September 1986) merupakan seorang aktor berkebangsaan Indonesia. Melalui film pertamanya dengan judul 7 Hati 7 Cinta 7 Wanita, ia berhasil masuk nominasi Aktor Pendatang Baru Terbaik di penghargaan Indonesian Movie Awards 2011. Filmografi Film Sebagai pemeran Tahun Judul Peran Catatan 2011 7 Hati 7 Cinta 7 Wanita Acin Catatan (Harian) Si Boy ...

Julianne MooreMoore di Festival Film Internasional Venice ke-66, September 2009LahirJulie Anne Smith3 Desember 1960 (umur 63)Fort Bragg, North Carolina, Amerika SerikatKebangsaanBritania Raya-Amerika SerikatPekerjaanaktrisPenulis buku anak-anakTahun aktif1983 - sekarangSuami/istriJohn Gould Rubin (m. 1986–1995) Bart Freundlich (m. 2003) Julianne Moore (Julie Anne Smith; lahir 3 Desember 1960...

PemberitahuanTemplat ini mendeteksi bahwa artikel bahasa ini masih belum dinilai kualitasnya oleh ProyekWiki Bahasa dan ProyekWiki terkait dengan subjek. Perhatian: untuk penilai, halaman pembicaraan artikel ini telah diisi sehingga penilaian akan berkonflik dengan isi sebelumnya. Harap salin kode dibawah ini sebelum menilai. {{PW Bahasa|importance=|class=}} Terjadi [[false positive]]? Silakan laporkan kesalahan ini. 08.45, Sabtu, 30 Maret, 2024 (UTC) • hapus singgahan Seban...

Pos Metro BatamTipeSurat kabar harianFormatKoranPemilikJawa Pos GroupPendiriJawa Pos GroupPenerbitPT Batam Metro MediaPemimpin redaksiRinaldyDiterbitkan14 Februari 2000; 24 tahun lalu (2000-02-14)BahasaBahasa IndonesiaPusatKomplek Ruko Mega Legenda E1 No.2, Baloi Permai, Batam Kota, Batam, Kepulauan Riau 29444Situs webposmetro.co Pos Metro Batam adalah sebuah surat kabar harian tertua dengan sirkulasi terbesar nomor satu yang terbit di Batam sementara surat kabar tertua di Batam untuk be...

Katedral Sofia di Harbin. Keuskupan Harbin adalah sebuah keuskupan dalam Gereja Ortodoks Timur yang didirikan di Manchuria untuk mendukung sejumlah besar penganut Rusia yang menetap di Manchuria. Mula-mula, para pengamut tersebut datang untuk mendukung Rusia membangun dan menjalankan Perkeretaapian Tiongkok Timur dan, yang kedua, kabur dari rezim Bolshevik di Rusia setelah Perang Saudara Rusia pada 1920. Keuskupan tersebut resmi dibentuk pada awal 1920-an oleh Gereja Ortodoks Rusia di Luar Ru...

Voce principale: L.R. Vicenza Virtus. L.R. Vicenza VirtusStagione 2018-2019Sport calcio Squadra Vicenza Allenatore Giovanni Colella (1ª-19ª) Michele Serena (20ª-28ª) Giovanni Colella (29ª-38ª e play-off) All. in seconda Moreno Greco (1ª-19ª giornata) Davide Zanon (20ª-28ª giornata) Moreno Greco (29ª-38ª) Presidente Stefano Rosso Serie C8º posto (ai playoff) Coppa Italia2º turno Coppa Italia Serie CSemifinale Maggiori presenzeCampionato: Zonta, Grandi (27)Totale: Zonta (36)...

イスラームにおける結婚(イスラームにおけるけっこん)とは、二者の間で行われる法的な契約である。新郎新婦は自身の自由な意思で結婚に同意する。口頭または紙面での規則に従った拘束的な契約は、イスラームの結婚で不可欠だと考えられており、新郎と新婦の権利と責任の概要を示している[1]。イスラームにおける離婚は様々な形をとることができ、個�...
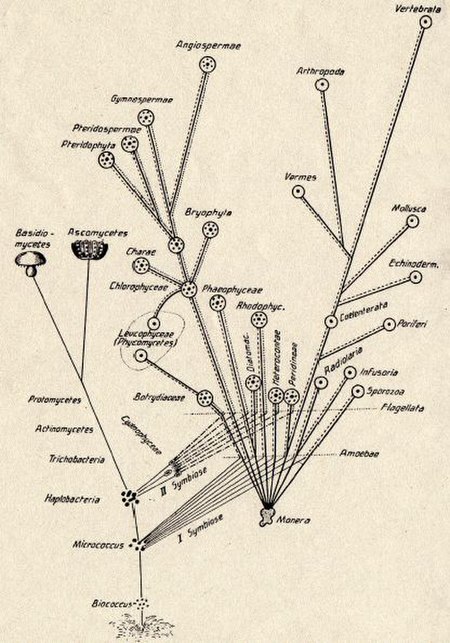
Evolutionary theory holding that eukaryotic organelles evolved through symbiosis with prokaryotes In the theory of symbiogenesis, a merger of an archaean and an aerobic bacterium created the eukaryotes, with aerobic mitochondria; a second merger added chloroplasts, creating the green plants. The original theory by Lynn Margulis proposed an additional preliminary merger, but this is poorly supported and not now generally believed.[1] Symbiogenesis (endosymbiotic theory, or serial endo...

追晉陸軍二級上將趙家驤將軍个人资料出生1910年 大清河南省衛輝府汲縣逝世1958年8月23日(1958歲—08—23)(47—48歲) † 中華民國福建省金門縣国籍 中華民國政党 中國國民黨获奖 青天白日勳章(追贈)军事背景效忠 中華民國服役 國民革命軍 中華民國陸軍服役时间1924年-1958年军衔 二級上將 (追晉)部队四十七師指挥東北剿匪總司令部參謀長陸軍�...

War memorial in the City of London London Troops War MemorialUnited KingdomThe memorial in 2010For Men of London who fought in World War I and World War IIUnveiled12 November 1920Location51°30′49″N 0°05′17″W / 51.513508°N 0.088057°W / 51.513508; -0.088057Royal Exchangenear City of LondonDesigned byAlfred DruryTO THE // IMMORTAL HONOUR // OF THE OFFICERS // NON-COMMISSIONED // OFFICERS AND MEN // OF LONDON // WHO SERVED THEIR // KING AND EMPIRE // ...

UQCRC1 المعرفات الأسماء المستعارة UQCRC1, D3S3191, QCR1, UQCR1, ubiquinol-cytochrome c reductase core protein I, ubiquinol-cytochrome c reductase core protein 1, PKNPY معرفات خارجية الوراثة المندلية البشرية عبر الإنترنت 191328 MGI: MGI:107876 HomoloGene: 2525 GeneCards: 7384 علم الوجود الجيني الوظيفة الجزيئية • ubiquinol-cytochrome-c reductase activity• GO:0032403 protein-containing comp...

2001 video game For the 2013 version of RuneScape, see Old School RuneScape. 2001 video gameRuneScapeDeveloper(s)JagexPublisher(s)JagexDesigner(s)Andrew GowerPaul GowerComposer(s)Ian TaylorAdam BondJames HanniganPlatform(s)WindowsmacOSLinuxAndroidiOSRelease4 January 2001[1]Genre(s)Massively multiplayer online role-playing gameMode(s)Multiplayer RuneScape is a fantasy massively multiplayer online role-playing game (MMORPG) developed and published by Jagex, released in January 2001. Run...

Le cinque più alte cariche dello Stato: da sinistra, Meloni, La Russa, Mattarella, Fontana e Sciarra (2 giugno 2023) Le Alte cariche dello Stato della Repubblica Italiana sono le cinque cariche più rilevanti del sistema costituzionale italiano; in funzione dell'ordine di protocollo sono[1]: Presidente della Repubblica Il Presidente del Senato della Repubblica e il Presidente della Camera dei deputati (ha la precedenza il più anziano) Presidente del Consiglio dei ministri Presidente...

Retired Pakistani squash player For other uses, see Jahangir Khan (disambiguation). Jahangir KhanJahangir Khan at the 2018 Asian AwardsNickname(s)JKCountryPakistanBorn (1963-12-10) 10 December 1963 (age 60)Karachi, PakistanRetired1993Racquet usedUnsquashableMen's singlesHighest rankingNo. 1World OpenW (1981, 1982, 1983, 1984, 1985, 1988) Medal record Men's squash Representing Pakistan World Championships 1981 Toronto Singles 1982 Birmingham Singles 1983 Munich Singles 198...

Ульрих Верницнем. Ulrich Wernitz Прозвище Pipifax Дата рождения 21 января 1921(1921-01-21) Место рождения Йессен, Виттенберг, Саксония-Анхальт, Германия Дата смерти 23 декабря 1980(1980-12-23) (59 лет) Место смерти Фюрстенфельдбрук, Верхняя Бавария, Бавария, ФРГ Род деятельности лётчик-ас Пр�...

Grekland TV-stationEllinikí Radiphonía Tileórassi (ERT)FramträdandenAntal framträdanden44 (2024)Debutår1974Bästa resultat1:a, 2005Sämsta resultat38:a, 2016Poäng genom tiderna3 399 (2024) endast finalerExterna länkarERT-sidaGreklands sida på Eurovision.tv Sakis Rouvas i Istanbul (2004) Kalomira i Belgrad (2008) Koza Mostra & Agathonas Iakovidis i Malmö (2013). Argo i Stockholm (2016). Demy i Kiev (2017). Katerine Duska i Tel Aviv (2019). Grekland debuterade i Eurovision Song Co...

AFC Champions League TwoAltri nomi(EN) ACL Two Sport Calcio TipoClub FederazioneAFC ContinenteAsia OrganizzatoreAsian Football Confederation TitoloCampione della AFC Champions League Two CadenzaAnnuale Aperturaluglio Chiusuramaggio Partecipanti32 squadre (2024-25) Formulafase a gironi, poi eliminazione A/R con ottavi, quarti, semifinale e finale. Sito Internetthe-afc.com StoriaFondazione2004 Numero edizioni20 Detentore C.C. Mariners Record vittorie Kuwait SC Al-Quwa Al-Jawiya (...















![{\displaystyle {\mathcal {T}}:[a,b]\mapsto \left[a,a+{\frac {b-a}{3}}\right]\cup \left[b-{\frac {b-a}{3}},b\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4972668c274eadb968814f5bc4102b6c9a5087ad)
![{\displaystyle \scriptstyle \left[a,a+{\frac {b-a}{3}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c509d55a2a347c5f613a5d70113d67fa2f9e4e84)
![{\displaystyle \scriptstyle \left[b-{\frac {b-a}{3}},b\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4e6f0fb382442becfa07c0ffdf42bdeac875a5bc)

