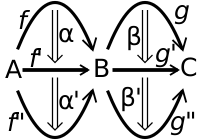
2-catégorie
|
Read other articles:

Jacques VergèsDalam pengadilan Khieu Samphan pada 2011Lahir(1925-03-05)5 Maret 1925Ubon Ratchathani, Kerajaan Rattanakosin, Siam (sekarang Thailand)Meninggal15 Agustus 2013(2013-08-15) (umur 88)Paris, PrancisKebangsaanPrancis dan AljazairPendidikanGelar hukum Universitas ParisPekerjaanPengacaraDikenal atasPengacara yang mewakili para penjahat perang terkenal[1]Suami/istriDjamila BouhiredAnakJacques-Loys Vergès (1951), Meriem Vergès (1967), Liess Vergès (1969)Orang tuaRaymond...

العلاقات السودانية السويسرية السودان سويسرا السودان سويسرا تعديل مصدري - تعديل العلاقات السودانية السويسرية هي العلاقات الثنائية التي تجمع بين السودان وسويسرا.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية للدولتين: وجه المقا...

The Imperial Trans-Antarctic Expedition was an attempt to cross the Antarctic continent led by Ernest Shackleton. The personnel were divided into two groups: the Weddell Sea party consisting of the men who would attempt the crossing and their support, and the Ross Sea party whose job it was to lay stores on the far side of the Pole for the members of the Weddell Sea party who would make the crossing. Both arms of the expedition had a final complement of 28 men. The Weddell Sea party's ship En...

The European Commission's programme for education, training, youth and sport Logo of the current Erasmus+ programme (2021–2027) The Erasmus Programme (EuRopean Community Action Scheme for the Mobility of University Students)[1] is a European Union (EU) student exchange programme established in 1987.[2][3] Erasmus+, or Erasmus Plus, is the new programme combining all the EU's current schemes for education, training, youth and sport, which was started in January 2014. ...

Sumber referensi dari artikel ini belum dipastikan dan mungkin isinya tidak benar. Mohon periksa, kembangkan artikel ini, dan tambahkan sumber yang benar pada bagian yang diperlukan. (Pelajari cara dan kapan saatnya untuk menghapus pesan templat ini) WaringinjayaDesaNegara IndonesiaProvinsiJawa BaratKabupatenBekasiKecamatanKedungwaringinKode pos17546Kode Kemendagri32.16.12.2002 Luas492,14 HaJumlah penduduk+/-27.093 jiwa(2021)Kepadatan- Untuk kegunaan lain, lihat Waringinjaya (disambiguas...

A questa voce o sezione va aggiunto il template sinottico {{Nazionale sportiva}} Puoi aggiungere e riempire il template secondo le istruzioni e poi rimuovere questo avviso. Se non sei in grado di riempirlo in buona parte, non fare nulla; non inserire template vuoti. Novella Calligaris, prima medagliata italiana ai Giochi olimpici Domenico Fioravanti premiato al Quirinale per gli ori di Sydney 2000 Domenico Fioravanti e Davide Rummolo a Sydney 2000 con il Commissario F.I.N...

Bulgarian RhapsodyPoster rilis teatrikalSutradaraIvan NitchevProduserLeon EderyMoshe EderyNissim LevyShaul ScherzeDitulis olehYurii DachevTatyana GranitovaJean Pierre MagroIvan NitchevPemeranStefan PopovKristiyan MakarovAnjela NedyalkovaPenata musikStephan DimitrovSinematograferAddie ReissPenyuntingTatyana BogdanovaIsaac SehayekDistributorCinepaz EOODCinisimaTanggal rilis Maret 2014 (2014-03) Durasi108 menitNegaraBulgariaIsraelBahasaBulgariaAnggaran1.8 juta leva Bulgarian Rhapsody ...

Turkish public university located in Marmara, İstanbul, Turkey This article contains content that is written like an advertisement. Please help improve it by removing promotional content and inappropriate external links, and by adding encyclopedic content written from a neutral point of view. (July 2019) (Learn how and when to remove this message) Marmara UniversityMarmara ÜniversitesiTypePublicEstablished1883: Hamidiye Ticaret Mekteb-i Âlis 1959: Istanbul Economy and Commerce Academy 1982...

Joe Mauer Mauer nel 2017 Nazionalità Stati Uniti Altezza 196 cm Peso 102 kg Baseball Ruolo Ricevitore, Prima base, Battitore designato Termine carriera 2018 CarrieraSquadre di club 2004-2018 Minnesota TwinsNazionale 2013 Stati Uniti Statistiche Batte sinistro Lancia destro Media battuta ,306 Valide 2 123 Punti battuti a casa 923 Fuoricampo 143 Punti 1 018 Basi totali 3 040 Basi rubate 52 Palmarès Trofeo Vittorie MVP dell'American League 1 All-Star 6 Per maggiori d...

Wo Gott der Herr nicht bei uns hältBWV 178Chorale cantata by Johann Sebastian BachJustus Jonas, the author of the hymnOccasionEighth Sunday after TrinityChoraleWo Gott der Herr nicht bei uns hältby Justus JonasPerformed30 July 1724 (1724-07-30): LeipzigMovements7Vocal SATB choir solo: alto, tenor and bass Instrumentalcorno da caccia2 oboes2 oboes d'amore2 violinsviolacontinuo Wo Gott der Herr nicht bei uns hält (Where God the Lord stands with us not),[1] BWV 178...

هذه المقالة بحاجة لصندوق معلومات. فضلًا ساعد في تحسين هذه المقالة بإضافة صندوق معلومات مخصص إليها. هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (أكتوبر 2015) العامل السماعي هو العامل الذي يصح أن يقال فيه: هذا يعمل كذ...

Language family of Liberia and Ivory Coast This article should specify the language of its non-English content, using {{lang}}, {{transliteration}} for transliterated languages, and {{IPA}} for phonetic transcriptions, with an appropriate ISO 639 code. Wikipedia's multilingual support templates may also be used. See why. (December 2021) KruGeographicdistributionIvory Coast, Liberia, Burkina FasoLinguistic classificationNiger–Congo?...

Canadian actor (1946–2024) For the Episcopal bishop, see Alan Scarfe (bishop). Alan ScarfeAlan Scarfe, 2005BornAlan John Scarfe(1946-06-08)8 June 1946Harpenden, EnglandDied28 April 2024(2024-04-28) (aged 77)Longueuil, Quebec, CanadaNationalityCanadianOccupation(s)Actor, stage director, authorYears active1962–2007Spouse Barbara March (m. 1979; died 2019)ChildrenJonathan Scarfe Alan John Scarfe[1] (8 June 1946 – 28 Apri...

Branch of the Salishan languages of western North America For details of the cultural group, see Coast Salish peoples.This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Coast Salish languages – news · newspapers · books · scholar · JSTOR (October 2023) (Learn how and when to remove this message)Coast SalishGeog...

Professional wrestling roster division, referred to as brands, in WWE RawLogo for the brand and the WWE Raw television program as of September 30, 2019Product typeProfessional wrestlingSports entertainmentOwnerWWEProduced byPaul Triple H LevesqueBruce PrichardCountryUnited StatesIntroducedMarch 25, 2002 (first split)July 19, 2016 (second split)DiscontinuedAugust 29, 2011 (first split)Related brandsSmackDownECWNXT205 LiveNXT UKTaglineMust be Monday[1] Raw is a brand of the America...

Former director of the Federal Bureau of Investigation (born 1960) Comey redirects here. For other people with the surname, see Comey (surname). Not to be confused with James Comer (disambiguation). James Comey7th Director of the Federal Bureau of InvestigationIn officeSeptember 4, 2013 – May 9, 2017PresidentBarack ObamaDonald TrumpDeputySean M. JoyceMark F. GiulianoAndrew McCabePreceded byRobert MuellerSucceeded byChristopher A. Wray31st United States Deputy Attorney GeneralIn off...

Defunct multi-sport event Asian Indoor GamesOfficial logo of the GamesAbbreviationAIGFirst event2005 Asian Indoor Games in Bangkok, ThailandOccur everytwo yearsLast event2009 Asian Indoor Games in Hanoi, Vietnam Games 2005 2007 2009 The Asian Indoor Games were a multi-sport event that was contested every two years among athletes representing countries from Asia. The games were regulated by the Olympic Council of Asia. The first games were held in 2005 in Bangkok, Thailand. The competition con...

Municipality in Quezon, Philippines Municipality in Calabarzon, PhilippinesPagbilaoMunicipalityMunicipality of PagbilaoFrom top, left to right : St. Catherine of Alexandria Parish Church • Zigzag Road, Quezon National Forest Park • Pueblo La Playa Resort FlagMap of Quezon with Pagbilao highlightedOpenStreetMapPagbilaoLocation within the PhilippinesCoordinates: 13°58′19″N 121°41′13″E / 13.972°N 121.687°E / 13.972; 121.687CountryPhilippinesRegionCalabarzo...

Battle of GrčaricePart of World War IIDate7—10 September 1943LocationGrčarice, German occupied Yugoslavia, modern-day Slovenia45°39′5.78″N 14°45′20.02″E / 45.6516056°N 14.7555611°E / 45.6516056; 14.7555611Result Partisan victoryBelligerents Slovene Chetniks Slovene PartisansCommanders and leaders Karl Novak Danilo Borut Koprivica Pavle Vošmar Vidmar Milan Kranjc Kajtimar Jaka Avšič Vinko Šumrada-RadošUnits involved Blue Guard:Dolenjska Chetnik Deta...

Ḥarrat Lunayyir (Arab: حَرَّة لُنَيِّر) adalah dataran lava di barat laut Arab Saudi.[1] Pada tahun 2009 terjadi banyak gempa bumi kecil di wilayah tersebut;[2] 2.289 orang dievakuasi dari wilayah tersebut.[3] Retakan terbuka di permukaan, dan area tersebut sekarang mungkin dianggap aktif secara vulkanik. Pemandangan Harrat Lunayyir dari Pesawat Ulang Alik Referensi ^ Global Volcanism Program - Harrat Lunayyir - Summary. Volcano.si.edu. Diakses tanggal ...