Fraktaali
|
Read other articles:

Partai Liberal Kanada Parti libéral du CanadaSingkatanLPC (bahasa Inggris)PLC (bahasa Prancis)Ketua umumJustin TrudeauPresidenSuzanne CowanDibentuk1861; 162 tahun lalu (1861)[a]IdeologiLiberalisme (Kanada)Liberalisme sosial[1]Afiliasi internasionalLiberal InternationalSitus webliberal.ca Partai Liberal Kanada (bahasa Inggris: Liberal Party of Canada, bahasa Prancis: Parti libéral du Canada) adalah sebuah partai politik beraliran tengah sampai kiri tengah di Kanada....

Sedative–hypnotic drug withdrawn due to recreational abuse MethaqualoneClinical dataPronunciation/mɛθəˈkweɪloʊn/ Trade namesBon-Sonnil, Dormogen, Dormutil, Mequin, Mozambin, Pro Dorm, Quaalude, Somnotropon, Torinal, Tuazolona Methaqualone hydrochloride: Cateudyl, Dormir, Hyptor, Melsed, Melsedin, Mequelon, Methasedil, Nobadorm, Normorest, Noxybel, Optimil, Optinoxan, Pallidan, Parest, Parmilene, Pexaqualone, Renoval, Riporest, Sedalone, Somberol, Somnifac, Somnium, Sopor, Sovelin...

Jan RaasJan Raas sur le podium du championnat du monde de 1979InformationsNaissance 8 novembre 1952 (71 ans)HeinkenszandNationalité néerlandaiseDistinction Cycliste néerlandais de l'annéeÉquipes professionnelles 1975TI-Raleigh1976TI-Raleigh-Campagnolo1977Frisol-Thirion-Gazelle1978-1979TI-Raleigh-Mac Gregor1980-1981TI-Raleigh-Creda1982-1983TI-Raleigh-Campagnolo1984-05.1985Kwantum Hallen-Decosol-YokoÉquipes dirigées 05.1985-1986Kwantum Hallen-Decosol-Yoko1987Superconfex-Kwantum Hall...

Social movement in the United States For other uses, see Civil rights movement (disambiguation). Part of a series onAfrican Americans History Periods Timeline Atlantic slave trade Abolitionism in the United States Slavery in the colonial history of the US Revolutionary War Antebellum period Slavery and military history during the Civil War Reconstruction era Politicians Juneteenth Civil rights movement (1865–1896) Jim Crow era (1896–1954) Civil rights movement (1954–1968) Black power mo...

2017 American filmAxisFilm posterDirected byAisha TylerScreenplay byEmmett HughesStory byEmmett HughesStephen MorrisseyProduced byR. Vaughn GillVertel ScottBarry SondersAisha TylerStarringEmmett HughesEmily Bett RickardsAmber NashPaula MalcomsonJonathan SadowskiJean-Luc BilodeauCinematographyLowell A. MeyerEdited byJohn QuinnAisha TylerMusic bySilversun PickupsProductioncompanyHot MachineDistributed byGiant InteractiveRelease dateApril 7, 2017Running time85 minutesCountryUnited StatesLanguage...

Documentary television series owned by A&E Networks This article may contain an excessive number of citations. Please help remove low-quality or irrelevant citations. (November 2019) (Learn how and when to remove this template message) BiographyGenreDocumentaryCreated byDavid L. WolperPresented byMike Wallace (1961–1963)David Janssen (1979)Peter Graves (1987–1999)Jack Perkins (1994–1999)Harry Smith (1999–2002)Neil Ross (2003–2006)Country of originUnited StatesOriginal languageEn...

Election in Massachusetts Main article: 1980 United States presidential election 1980 United States presidential election in Massachusetts ← 1976 November 4, 1980 1984 → Nominee Ronald Reagan Jimmy Carter John B. Anderson Party Republican Democratic Anderson Coalition [a] Home state California Georgia Illinois Running mate George H. W. Bush Walter Mondale Patrick Lucey Electoral vote 14 0 0 Popular vote 1,057,631 1,053,802 382,539 Perce...

District in Mondulkiri, CambodiaKaev Seima District ស្រុកកែវសីមាDistrictDistrict location in Mondulkiri ProvinceCoordinates: 12°21′46″N 106°49′07″E / 12.3628°N 106.8187°E / 12.3628; 106.8187Country CambodiaProvinceMondulkiriPopulation (1998) • Total8,854[1]Time zoneUTC+7 (ICT)Geocode1101 Kaev Seima (Khmer: កែវសីមា) is a district (srok) located in Mondulkiri Province, in Cambodia. References...
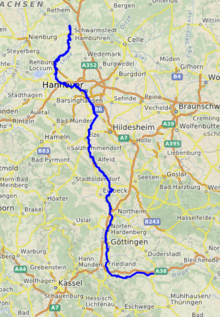
Disambiguazione – Se stai cercando altri significati, vedi Leine (disambigua). LeineIl corso del Leine a Sarstedt-RutheStato Germania Länder Turingia Bassa Sassonia Lunghezza281 km Portata media5,3 m³/s Bacino idrografico6 512 km² Altitudine sorgente340 m s.l.m. Sfocianel fiume Aller presso Schwarmstedt Modifica dati su Wikidata · Manuale Il corso del Leine Il Leine (in tedesco [ˈlaɪnə]ⓘ) è un fiume tedesco che scorre nei Länder della Turingia e della Ba...

Province of Ecuador Province in EcuadorEl Oro Provincia de El OroProvinceProvince of El Oro FlagCantons of El Oro ProvinceCountryEcuadorEstablishedApril 23, 1884CapitalMachalaCantonsList of CantonsArea • Total5,873 km2 (2,268 sq mi)Highest elevation[1]3,590 m (11,780 ft)Lowest elevation0 m (0 ft)Population (2022 census)[2] • Total714,592 • Density120/km2 (320/sq mi) • Populat...

Species of venomous pit viper of the Ryukyu Islands of Japan Protobothrops flavoviridis Conservation status Least Concern (IUCN 3.1)[1] Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Chordata Class: Reptilia Order: Squamata Suborder: Serpentes Family: Viperidae Genus: Protobothrops Species: P. flavoviridis Binomial name Protobothrops flavoviridis(Hallowell, 1861) Synonyms[2] Bothrops flavoviridis Hallowell, 1861 Trimeresurus riukiuanus Hilgend...

Former Royal Air Force station in North Rhine-Westphalia, Germany This article includes a list of references, related reading, or external links, but its sources remain unclear because it lacks inline citations. Please help improve this article by introducing more precise citations. (February 2013) (Learn how and when to remove this message) RAF Geilenkirchen Geilenkirchen, North Rhine-Westphalia in GermanyRAF GeilenkirchenShown within GermanyCoordinates50°57′36.7″N 6°2′32.6″E&...

UFC mixed martial arts event in 2019 UFC Fight Night: Błachowicz vs. SantosThe poster for UFC Fight Night: Błachowicz vs. SantosInformationPromotionUltimate Fighting ChampionshipDateFebruary 23, 2019 (2019-02-23)VenueO2 ArenaCityPrague, Czech RepublicAttendance16,583[1]Total gate$1,606,176[1]Event chronology UFC on ESPN: Ngannou vs. Velasquez UFC Fight Night: Błachowicz vs. Santos UFC 235: Jones vs. Smith UFC Fight Night: Błachowicz vs. Santos (also known as...

حكومة حسين بن ناصر الأولىمعلومات عامةرئيس الحكومة حسين بن ناصرالتكوين 21-4-1963النهاية 9-7-1963المدة شهران و18 يومًاحكومة سمير الرفاعي الخامسةحكومة حسين بن ناصر الثانيةتعديل - تعديل مصدري - تعديل ويكي بياناتجزء من سلسلة مقالات سياسة الأردنالأردن الدستور الدستور حقوق الإنسان �...

منليك الثاني، امبراطور إثيوپيا. اتفاقية أديس أبابا بين بريطانيا وإثيوبيا، الموقعة في 15 مايو 1902م، ووقعها بريطانيا بالنيابة عن السودان، وأهم ما فيها المادة الثالثة التي تنص على: إن الإمبراطور الإثيوبي منليك الثاني يعد بألا يبني أو يسمح ببناء أي أعمال على النيل الأزرق وبحير�...

ماكس تيشلر معلومات شخصية الميلاد 1906بوسطن الوفاة 18 مارس 1989 (82 سنة)ميدلتاون الجنسية أمريكي عضو في الأكاديمية الأمريكية للفنون والعلوم، والأكاديمية الوطنية للعلوم الحياة العملية المؤسسات جامعة هارفارد، ميرك آند كو، جامعة وزليان المدرسة الأم جامعة تافتس مشرف الدكتور...

此條目没有列出任何参考或来源。 (2013年8月15日)維基百科所有的內容都應該可供查證。请协助補充可靠来源以改善这篇条目。无法查证的內容可能會因為異議提出而被移除。 德斯坎苏Descanso市镇德斯坎苏在巴西的位置坐标:26°49′29″S 53°30′06″W / 26.8246854°S 53.5017586°W / -26.8246854; -53.5017586国家巴西州圣卡塔琳娜州面积 • 总计285.571 平方公里(11...

Questa voce sull'argomento università degli Stati Uniti d'America è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. University of Vermont(EN) The University of Vermont and State Agricultural College UbicazioneStato Stati Uniti CittàBurlington Dati generaliNome latinoUniversitas Viridis Montiss SoprannomeCatamounts (sport); UVM MottoStudiis et Rebus Honestis Fondazione1791 FondatoreIra Allen TipoUniversità pubblica RettoreDaniel Mark Fo...

У этого человека испанская фамилия; здесь Маркес — фамилия отца, Альварес — фамилия матери. Эта статья о футболисте, статья о боксёре называется Рафаэль Маркес (боксёр) Рафаэль Маркес Общая информация Полное имя Рафаэль Маркес Альварес Прозвище Мичоаканский Кайзер (и...

Các vương triều Ai Cập cổ đại Tất cả các năm (cột phải ngoài cùng) đều là TCN Sơ triều đại Vương triều thứ Nhất I c. 3150–2890 Vương triều thứ Hai II 2890–2686 Cổ Vương quốc Vương triều thứ Ba III 2686–2613 Vương triều thứ Tư IV 2613–2498 Vương triều thứ Năm V 2498–2345 Vương triều thứ Sáu VI 2345–2181 Chuyển tiếp thứ Nhất Vương triều thứ Bảy và Tám VII/VIII 2181–2160 Vương tri�...




