Bat
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Read other articles:

Gen Shoji Kembalinya Belgia yang luar biasa melawan Jepang, 2018Informasi pribadiNama lengkap Gen ShojiTanggal lahir 11 Desember 1992 (umur 31)Tempat lahir Prefektur Hyogo, JepangTinggi 182 m (597 ft 1 in)Posisi bermain BekInformasi klubKlub saat ini Kashima AntlersNomor 3Karier junior2008–2010 Yonago Kita High SchoolKarier senior*Tahun Tim Tampil (Gol)2011– Kashima Antlers 144 (7)Tim nasional‡2015- Jepang 11 (0) * Penampilan dan gol di klub senior hanya dihitung da...

Pelayanan Kesehatan Nasional Britania RayaNational Health ServiceLogo NHS EnglandInformasi lembagaDibentuk5 Juli 1948; 75 tahun lalu (1948-07-05)Pegawai1.700.000Anggaran tahunan£139,3 miliar GBP (2019/20)Departemen induk Departemen Kesehatan dan Layanan Sosial (Inggris)Direktorat Kesehatan dan Layanan Sosial (Skotlandia)Pemerintah Wales (Wales)Departemen Kesehatan (Irlandia Utara)Lembaga bawahanNHS EnglandNHS ScotlandNHS WalesHSC di Irlandia UtaraSitus webwww.nhs.uk Pelayanan Kesehatan ...

Angsa Terancam karya Jan Asselijn,1650 Legenda klasik menyatakan bahwa angsa menyanyi saat mati dimasukkan dalam salah satu Fabel Aesop, bernomor 399 dalam Perry Index.[1] Fabel tersebut juga mengenalkan peribahasa antitesis antara angsa berleher panjang dan angsa berleher pendek yang menimbulkan pernyataan seperti ‘Setiap manusia berpikir angsa leher pendek miliknya sendiri adalah angsa leher panjang’, dalam merujuk kepada ketepihakan buta dan 'Semua angsa leher panjangku berubah...

Cycling race Round 5Women's individual pursuit2008–2009 UCI Track Cycling World Cup Classics, race 5/5Race detailsDates13 February 2009Stages1Distance3 km (1.864 mi)Winning time3:38.870Medalists Gold Ellen van Dijk (NED) Silver Tara Whitten (CAN) Bronze Joanna Rowsell (GBR)← Round 1Round 2Round 3Round 4 Round 5 → The fifth round of the women's individual pursuit of the 2008–2009 UCI Track ...

Tupai kerdil[1] Tupaia minor Status konservasi Risiko Rendah (IUCN 3.1)[2] Klasifikasi ilmiah Kerajaan: Animalia Filum: Chordata Kelas: Mammalia Ordo: Scandentia Famili: Tupaiidae Genus: Tupaia Spesies: T. minor Nama binomial Tupaia minorMiller, 1903 Peta persebaran Tupai kecil atau disebut juga tupai kerdil (Tupaia minor) adalah salah satu spesies tupai yang berada dalam famili Tupaiidae.[1] Spesies ini adalah spesies asli yang berada di wilayah Thailand, M...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Strasburg, Virginia – news · newspapers · books · scholar · JSTOR (February 2019) (Learn how and when to remove this template message) Town in Virginia, United StatesStrasburg, VirginiaTownFront and western side of the former Strasburg Stone and Earthenware Ma...

John Stockton Posisi:Point guard Nomor Jersey:12 Tinggi:6 ft 1 in (1,85 m) Berat:170 pon (77 kg) Lahir: 26 Maret 1962 (umur 62)Spokane, Washington Informasi karier Tahun aktif: 1984–2003 NBA Draft: 1984 / Ronde: 1 / Pick: 16 Kuliah: Gonzaga Tim profesional {{{teams}}} Statistik karier Points 19,711 Assists 15,806 Steals 3,265 Stats @ Basketball-Reference.com Penghargaan 10x NBA All-Sta...

American musical comedy-drama television series (2009–2015) GleeGenre Musical Comedy drama Romantic comedy Teen drama Created by Ryan Murphy Brad Falchuk Ian Brennan ShowrunnerRyan MurphyStarring Dianna Agron Chris Colfer Jessalyn Gilsig Jane Lynch Jayma Mays Kevin McHale Lea Michele Cory Monteith Matthew Morrison Amber Riley Mark Salling Jenna Ushkowitz Heather Morris Mike O'Malley Naya Rivera Darren Criss Harry Shum Jr. Chord Overstreet Jacob Artist Melissa Benoist Blake Jenner Alex Newel...

Engelberto Iconte di BergStemma In caricaprima del 1160 - 1189 PredecessoreAdolfo II SuccessoreAdolfo III Nome completoEngelberto di Berg Nascitaprima metà del secolo XII MorteKovin, Banato, luglio 1189 PadreAdolfo II MadreIrmgarda di Schwarzenburg ConsorteMargherita di Gheldria FigliAdolfo eEngelberto Religionecattolico Engelberto I di Berg in tedesco: Engelbert I. (Berg) (prima metà del secolo XII – Kovin, luglio 1189) fu il terzo conte documentato (dal 1164) della contea di Berg,...
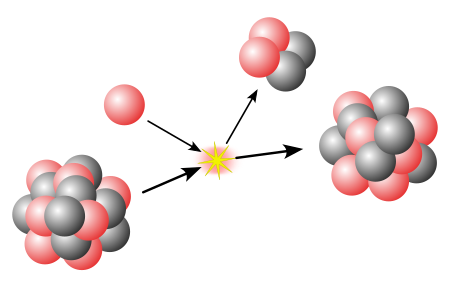
انشطار نوويمعلومات عامةصنف فرعي من إنشقاقتفاعل نووي جانب من جوانب فيزياء نووية سُمِّي باسم الانقسام الثنائي تسبب في اضمحلال نشاط إشعاعيحرارة زمن الاكتشاف أو الاختراع ديسمبر 1938 تعديل - تعديل مصدري - تعديل ويكي بيانات جزء من سلسلة مقالات حولفيزياء نوويةنشاط إشعاعي • انشطا�...

Ancient Roman style of inscription Quadrata redirects here. For the place in ancient Rome, see Roma quadrata. This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Roman square capitals – news · newspapers · books · scholar · JSTOR (February 2014) (Learn how and when to remove this message) A drawing and photograp...

Historical and descriptive outline of the American cable television industry This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Cable television in the United States – news · newspapers · books · scholar · JSTOR (February 2009) (Learn how and when to remove this message) Cable television first became available ...

2006 concert tour by Robbie Williams Close Encounters TourTour by Robbie WilliamsPromotional advert for the tourAssociated albumIntensive CareStart date10 April 2006End date18 December 2006Legs4No. of shows3 in Africa1 in Asia38 in Europe4 in South America2 in North America9 in Australia57 totalRobbie Williams concert chronology 2003 Tour(2003) Close Encounters Tour(2006) Take the Crown Stadium Tour(2013) The Close Encounters Tour was a concert tour by English recording artist, Robbie William...

United States income tax calculation This article is part of a series onTaxation in the United States Federal taxation Alternative minimum tax Capital gains tax Corporate tax Estate tax Excise tax Gift tax Generation-skipping transfer tax Income tax Payroll tax Internal Revenue Service (IRS) Internal Revenue Code (IRC) IRS tax forms Revenue by state History Constitutional authority Taxpayer standing Court Protest Evasion Resistance State and local taxation State income tax Property tax Sales ...

Stasiun Daishaka大釈迦駅Stasiun Daishiki pada Agustus 2007LokasiNamioka Daishaka Maeda 80, Aomori-shi, Aomori-ken 038-1301JepangKoordinat40°45′24.04″N 140°35′15.42″E / 40.7566778°N 140.5876167°E / 40.7566778; 140.5876167Operator JR EastJalur■ Jalur Utama ŌuLetak467.2 km dari FukushimaJumlah peron1 peron samping + 1 peron pulauInformasi lainStatusTanpa stafSitus webSitus web resmiSejarahDibuka1 Desember 1894Lokasi pada petaStasiun DaishakaLokasi di Pr...

Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber: Ketileng, Kramat, Tegal – berita · surat kabar · buku · cendekiawan · JSTORKetilengDesaNegara IndonesiaProvinsiJawa TengahKabupatenTegalKecamatanKramatKode pos52181Kode Kemendagri33.28.15.2006 Ketil...

American college sports rivalry School Old Dominion William & Mary Established 1930 1693 Location Norfolk Williamsburg Conference Sun Belt CAA Students (2019) 24,286 8,617 School Colors Slate Blue, Silver, & Light Blue Green & Gold Nickname Monarchs Tribe Varsity Teams 18 19 Battle for the Silver Mace Wins 2 1 75km50miles William & Mary Old Dominion Locations of Old Dominion and William & Mary. The Old Dominion–William & Mary rivalry (formerly known as the Battl...

Russian politician and former Ukrainian terrorist leader In this name that follows Eastern Slavic naming customs, the patronymic is Yurevich and the family name is Borodai. This article needs to be updated. Please help update this article to reflect recent events or newly available information. (September 2023) Alexander BorodaiАлександр БородайBorodai in 2017Member of the State DumaIncumbentAssumed office 12 October 2021First Deputy Prime Minister of Donetsk People's ...

Canadian politician The Hon.William Berrian VailMember of the Canadian Parliamentfor DigbyIn office1874–1877Preceded byEdwin Randolph OakesSucceeded byJohn Chipman WadeIn office1882–1887Preceded byJohn Chipman WadeSucceeded byJohn CampbellMember of the Nova Scotia House of Assembly for Digby CountyIn office1867–1874 Personal detailsBorn(1823-12-19)December 19, 1823Sussex Vale, Colony of New BrunswickDiedApril 10, 1904(1904-04-10) (aged 80)Dover, EnglandPolitical partyLiberalOther p...

Ravi GomatamRavi Gomatam, June, 2011BornJanuary 1950Alma materAnnamalai UniversityBITS PilaniUniversity of MumbaiScientific careerFieldsQuantum physics Ravi Veeraraghavan Gomatam (born in Chennai, India) is the director of Bhaktivedanta Institute (Berkeley and Mumbai) and the newly formed Institute of Semantic Information Sciences and Technology, Mumbai. He teaches graduate-level courses at these institutes. He was an adjunct professor at Birla Institute of Technology & Science (BIT...
