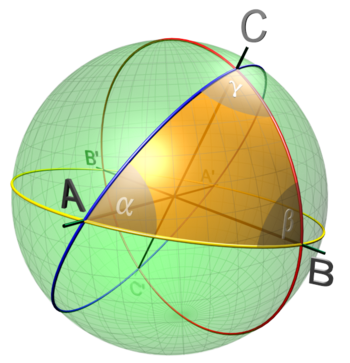
Trigonometría esférica
|
Read other articles:

A minister within the Cabinet of Victoria Minister for Education of VictoriaVictorian Coat of armsFlag of VictoriaIncumbentBen Carroll MPsince 2 October 2023Department of EducationStyleThe HonourableMember ofParliamentCabinetExecutive councilReports toPremierNominatorPremierAppointerGovernoron the recommendation of the PremierTerm lengthAt the Governor's pleasurePrecursor Minister of Education Minister for Education and Training Minister for School Education Inaugural holderRobert Ramsay...

Artikel ini perlu diterjemahkan dari bahasa Inggris ke bahasa Indonesia. Artikel ini ditulis atau diterjemahkan secara buruk dari Wikipedia bahasa Inggris. Jika halaman ini ditujukan untuk komunitas bahasa Inggris, halaman itu harus dikontribusikan ke Wikipedia bahasa Inggris. Lihat daftar bahasa Wikipedia. Artikel yang tidak diterjemahkan dapat dihapus secara cepat sesuai kriteria A2. Jika Anda ingin memeriksa artikel ini, Anda boleh menggunakan mesin penerjemah. Namun ingat, mohon tidak me...

Urban locality in Ternopil Oblast, Ukraine Urban-type settlement in Ternopil Oblast, UkraineHusiatyn ГусятинHusiatyn (in Polish)הוסיאַטין (in Yiddish)GusiatynUrban-type settlementView of the town FlagCoat of armsHusiatynLocation of Husiatyn in UkraineShow map of Ternopil OblastHusiatynHusiatyn (Ukraine)Show map of UkraineCoordinates: 49°04′14″N 26°11′37″E / 49.07056°N 26.19361°E / 49.07056; 26.19361Country UkraineOblastTernopil O...

Howard BayBorn(1912-05-03)3 May 1912Centralia, WashingtonDied21 November 1986(1986-11-21) (aged 74)Manhattan, New York City, U.S.OccupationDesigner Howard Bay (May 3, 1912 – November 21, 1986, New York City) was an American scenic, lighting and costume designer for stage, opera and film. He won the Tony Award for Best Scenic Design twice. Career Howard Bay's set and the fatal fire in the tenement that begins One-Third of a Nation, a Living Newspaper about housing produced by the Fe...
Act of the Parliament of Australia Native Title Act 1993Parliament of Australia Long title An Act about native title in relation to land or waters, and for related purposes.[1] CitationAct No. 110 of 1993 or Act No. 110 of 1993 as amendedTerritorial extentStates and territories of AustraliaRoyal assent24 December 1993[2]Status: Amended The Native Title Act 1993 (Cth) is a law passed by the Australian Parliament, the purpose of which is to provide a national system for the reco...

Световой годсв.год Две сферы с радиусами 1 и 10 световых лет в сравнении с расстояниями от Земли до ближайших известных звёзд; размеры самих звёзд увеличены для улучшения восприятия. Величина длина Система Астрономическая система единиц Тип основная Светово́й год (обозна...

Renato d'AlençonRenato d'Alençon raffigurato in un'incisione del XVII-XVIII secoloDuca d'AlençonStemma In carica8 settembre 1476 –1º novembre 1492 PredecessoreGiovanni II d'Alençon SuccessoreCarlo IV d'Alençon Altri titoliConte di Perche Nascita1454 MorteAlençon, 1º novembre 1492 DinastiaValois PadreGiovanni II d'Alençon MadreMaria d'Armagnac ConsorteMargherita di Lorena FigliCarloFrancescaAnna ReligioneCattolicesimo Conti e duchi d'Alençon Valois-Alençon Carlo II (132...

City in Mogilev Region, Belarus This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Babruysk – news · newspapers · books · scholar · JSTOR (February 2009) (Learn how and when to remove this message) City in Mogilev Region, BelarusBabruysk Бабруйск • БобруйскBobruyskCity FlagCoat of armsBabruysk...

19th race of the 2013 NASCAR Nationwide Series 2013 Indiana 250 Race details Race 19 of 33 of the 2013 NASCAR Nationwide SeriesDate July 27, 2013Official name 2nd Annual Indiana 250Location Speedway, Indiana, Indianapolis Motor SpeedwayCourse Permanent racing facility2.5 mi (4.0 km)Distance 100 laps, 250 mi (402.336 km)Scheduled Distance 100 laps, 250 mi (402.336 km)Average speed 134.61 miles per hour (216.63 km/h)Pole positionDriver Kyle Busch Joe Gibbs RacingTime 50.099Most laps ledDri...

27th Premier of Quebec (1996–2001) This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (February 2011) (Learn how and when to remove this message) The HonourableLucien BouchardPC GOQBouchard in June 201327th Premier of QuebecIn officeJanuary 29, 1996 – March 8, 2001MonarchElizabeth IILieutenant GovernorMartial AsselinJean-Louis RouxLise Thibau...

El NacionalNama lengkapClub Social, Cultural y Deportivo El NacionalJulukanPuros Criollos (Pure Criollos)Equipo Militar (Military team)La Maquina Roja (The Red Machine)Berdiri1 Juni 1964; 60 tahun lalu (1964-06-01)StadionEstadio Olímpico Atahualpa(Kapasitas: 40,948)KetuaCalmte. Angel Sarzosa AguirreManajerCarlos SevillaLigaSerie A20129thSitus webSitus web resmi klub Kostum Principal Kostum tandang Club Deportivo El Nacional adalah tim sepak bola profesional asal Ekuador yang bermuk...

Australian actress and comedian (born 1961) Magda SzubanskiAOSzubanski at Tropfest 2013BornMagdalene Mary Therese Szubanski[1][2] (1961-04-12) 12 April 1961 (age 63)Liverpool, EnglandNationalityAustralian[3][4][5]EducationSiena CollegeAlma materUniversity of MelbourneOccupationsActressauthorcomedianLGBT rights advocateYears active1986–presentNotable workEsme Cordelia Hoggett in Babe (1995) and its 1998 sequel Voice of Miss Viola in Happ...
Procurement process E-commerce Digital content Ebook Software Streaming media Retail goods and services Advertising Auctions Banking DVD-by-mail Distribution Food ordering Grocery Marketplace Pharmacy Ride-hailing Travel Online shopping Comparison shopping Social commerce Trading communities Wallet Mobile commerce Payment Ticketing Customer service Call centre Help desk Live support software E-procurement Purchase-to-pay Super-appsvte Purchase-to-pay, often abbreviated to P2P and also called ...

American descendants of Ulster Scots Not to be confused with Irish Americans or Irish Scottish people. This article is about American descendants of Ulster Scots. For ancestral group, see Ulster Scots people. Ethnic group Scot-Irish AmericansScots-Irish AmericansTotal population2,500,076 (0.7%) alone or in combination 977,075 (0.3%) Scot-Irish alone 2021 estimates, self-reported[1] Estimate of Scot-Irish total27,000,000 (2004)[2][3]Up to 9.2% of the U.S. population (20...

Talmudic scholar, posek and Sephardi Chief Rabbi of Israel from 1973 to 1983 MaranOvadia Yosefעובדיה יוסףRav Ovadia Yosef pictured at the Ohel Shem synagogue in Pardes KatzPersonalBornSeptember 24, 1920Baghdad, British occupied IraqDiedOctober 7, 2013(2013-10-07) (aged 93)JerusalemReligionJudaismNationalityIsraeliSpouseMargalit FattalChildren11, including Yitzhak Yosef, Ya'akov Yosef and Adina Bar-ShalomParent(s)Yaakov and Gorjiya OvadiaDenominationSephardi Haredi Judais...

大悟(だいご) 国土交通省のインタビューにて(2020年)。本名 山本 大悟(やまもと だいご)別名義 ダイ山本(ダイやまもと)[1]山本 大娯[2]生年月日 (1980-03-25) 1980年3月25日(44歳)出身地 岡山県笠岡市北木島血液型 B型身長 170 cm[3]言語 日本語方言 岡山弁関西弁最終学歴 岡山県立笠岡商業高等学校 卒業出身 オーディションコンビ名 千鳥相方 ノブ芸...

American judge (1933–2020) For the Australian rules footballer, see Kevin Duffy (footballer). For the British publisher, see Kevin Duffy (publisher). This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Kevin Duffy – news · newspapers · books · scholar · JSTOR (April 2020) (Learn how and when to remove this mes...

Pompa bahan bakar atau dikenal juga dengan nama Fuel Pump adalah salah satu komponen dalam sistem bahan bakar pada sebuah kendaraan atau mesin pembakaran dalam lainnya. Sebagian mesin tidak memerlukan pompa bahan bakar karena dari desainnya dan dengan gravitasi, bahan bakar akan mengalir dengan sendirinya dalam sistem bahan bakarnya. Sebagian yang lainnya harus menggunakan pompa untuk mengalirkan bahan bakar dari tangki bahan bakar. Pada mesin dengan menggunakan karburator, umumnya menggunaka...

2007 Bahamian general election ← 2002 2 May 2007 (2007-05-02) 2012 → All 41 seats of the Bahamian House of Assembly21 seats needed for a majority First party Second party Leader Hubert Ingraham Perry Christie Party FNM PLP Leader since 1992, 2005 1997 Leader's seat North Abaco Farm Road & Centreville Last election 7 seats, 17.50% 29 seats, 72.50% Seats won 23 18 Seat change 16 11 Popular vote 68,624 64,648 P...

صورة لتشريح أذن إنسان، بقرة، كلب، حصان، نمر، قط، وفئران، خنزير وخروف واوز هو موضح للعالم والراهب الألماني أثانيسيوس كيرتشر. العلاقة بين المسيحية والطب تعود إلى عصور المسيحية المبكرة إذ كان للمفاهيم المسيحية من الرعاية ومساعدة المرضى دور في تطوير الأخلاق الطبية.[1] أنش...