Teorema de Erdős-Szekeres
|
Read other articles:

Strada statale 587di CortemaggioreLocalizzazioneStato Italia Regioni Emilia-Romagna DatiClassificazioneStrada statale Inizioex SS 10 presso Piacenza FineCortemaggiore Lunghezza13,960[1] km Provvedimento di istituzioneD.M. 26/05/1969 - G.U. 177 del 15/07/1969[2] GestoreTratte ANAS: nessuna (dal 2001 la gestione è passata alla Provincia di Piacenza) Manuale La ex strada statale 587 di Cortemaggiore (SS 587), ora strada provinciale 587 R di Cortemaggiore (SP 587 R)[...

Coppa dei BalcaniSport Calcio CadenzaAnnuale StoriaFondazione1961 Soppressione1993-1994 Ultimo vincitore Samsunspor Record vittorie Beroe (4) Ultima edizioneCoppa dei Balcani 1993-1994 Modifica dati su Wikidata · Manuale La Coppa dei Balcani per club era un torneo internazionale di calcio disputato dalla stagione 1961 alla stagione 1993-94 e riservato ai club di Albania, Bulgaria, Grecia, Romania, Turchia e Jugoslavia. Indice 1 Storia 2 Albo d'oro 3 Partecipanti 4 Voci correla...

For other uses, see Laborec (disambiguation). River in Ukraine, SlovakiaLaborecLaborec at StrážskeLocationCountryUkraine, SlovakiaPhysical characteristicsSource • locationLaborec Highlands Mouth • locationLatorica • coordinates48°30′14″N 21°54′04″E / 48.504°N 21.901°E / 48.504; 21.901Length126 km (78 mi)Basin size4,523 km2 (1,746 sq mi)Basin featuresProgressionL...

This article is about the former Palestinian village in Tiberias Sub-district. For other uses, see El Mansurah (disambiguation). Village in Tiberias, Mandatory PalestineAl-Mansura المنصورةVillageEtymology: Building[1] 1870s map 1940s map modern map 1940s with modern overlay map A series of historical maps of the area around Al-Mansura, Tiberias (click the buttons)Al-MansuraLocation within Mandatory PalestineCoordinates: 32°53′29″N 35°25′01″E / 32.8913...

Ираклеониты — ученики гностика Ираклеона (II век). Упоминаются как особая секта Епифанием и Августином; при крещении и миропомазании они соблюдали обряд помазания елеем и при этом произносили воззвания на арамейском языке, которые должны были освободить душу от власт�...

Broadway theater in Manhattan, New York Virginia Theatre redirects here. For the theater in Champaign, Illinois, see Virginia Theatre (Champaign). August Wilson TheatreGuild Theatre, ANTA Theatre, Virginia TheatreShowing Slave Play, 2021Address245 West 52nd StreetManhattan, New York CityUnited StatesCoordinates40°45′48″N 73°59′03″W / 40.76333°N 73.98417°W / 40.76333; -73.98417OwnerJujamcyn TheatersTypeBroadwayCapacity1,222ProductionCabaretConstructionOpened...

Artikel ini perlu dikembangkan dari artikel terkait di Wikipedia bahasa Inggris. (Desember 2023) klik [tampil] untuk melihat petunjuk sebelum menerjemahkan. Lihat versi terjemahan mesin dari artikel bahasa Inggris. Terjemahan mesin Google adalah titik awal yang berguna untuk terjemahan, tapi penerjemah harus merevisi kesalahan yang diperlukan dan meyakinkan bahwa hasil terjemahan tersebut akurat, bukan hanya salin-tempel teks hasil terjemahan mesin ke dalam Wikipedia bahasa Indonesia. Ja...

Italian breed of mastiff Dog breedCane CorsoOther namesCane Corso ItalianoOriginItalyTraitsHeight Males 62–70 cm (24–28 in) Females 58–66 cm (23–26 in)Weight Males 45–50 kg (100–110 lb)[1] Females 40–45 kg (90–100 lb)[1]Kennel club standardsEnte Nazionale della Cinofilia Italiana standardFédération Cynologique Internationale standardDog (domestic dog) The Cane Corso[a] is an Italian breed of mastiff. It is usual...

Pinna nobilis Spesimen hidupf Pinna nobilis, di Levanto, Liguria (Italia) Klasifikasi ilmiah Kerajaan: Animalia Filum: Mollusca Kelas: Bivalvia Ordo: Pterioida Famili: Pinnidae Genus: Pinna Spesies: P. nobilis Nama binomial Pinna nobilisLinnaeus, 1758 Sinonim Pinna gigas Chemnitz Pinna nobilis adalah sebuah spesies besar dari kerang Laut Tengah, sebuah moluska bivalve laut dalam Pinnidae. Spesies tersebut dapat memiliki panjang sampai 120 cm (4 ft).[1] Penjelasan Spesi...

Negative of a convex function In mathematics, a concave function is one for which the value at any convex combination of elements in the domain is greater than or equal to the convex combination of the values at the endpoints. Equivalently, a concave function is any function for which the hypograph is convex. The class of concave functions is in a sense the opposite of the class of convex functions. A concave function is also synonymously called concave downwards, concave down, convex upwards...

Style of English sword dance This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Rapper sword – news · newspapers · books · scholar · JSTOR (April 2012) (Learn how and when to remove this message) Sallyport Rapper performing in Morpeth 1999. Rapper sword (also known as short sword dance) is a variation of sword ...
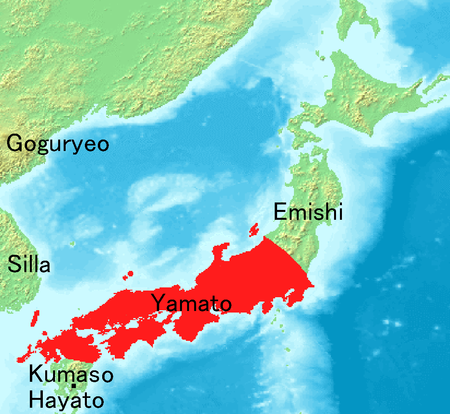
Period of Japanese history from c. 250 to 710 Further information on this topic: Kofun period and Asuka period This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Yamato period – news · newspapers · books · scholar · JSTOR (October 2013) (Learn how and when to remove this message) Part of a series on theHist...

Silla BersatuPaviliun AnapjiNama KoreaHangul통일 신라 Hanja統一新羅 Alih AksaraTong(-)il SillaMcCune–ReischauerT'ongil Silla Silla Bersatu (668 M -935 M) adalah masa saat Silla, salah satu dari Tiga Kerajaan Korea menaklukkan dan menyatukan Baekje pada tahun 660 dan Goguryeo pada tahun 668. Tahun 935, masa Silla Bersatu berakhir dan berganti oleh Dinasti Goryeo. Nama Bagian dari seri mengenai Sejarah Korea Prasejarah Zaman Jeulmun Zaman Mumun Kuno Gojoseon 2333 SM - 108 SM Jin Proto...

Quattro celebri e importanti filosofi esistenzialisti, da sinistra a destra, e dall'alto in basso: Kierkegaard, Dostoevskij, Nietzsche, Sartre L'esistenzialismo è una variegata e non omogenea corrente di pensiero che si è espressa in vari ambiti culturali e sociali umani, tra filosofia, letteratura, arti e costume, affermando, nell'accezione più comune del termine, il valore intrinseco dell'esistenza umana individuale e collettiva come nucleo o cardine di riflessione, diversamente da a...

This article is about the automobile engine. For the steam locomotive, see GWR Iron Duke Class. This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Iron Duke engine – news · newspapers · books · scholar · JSTOR (January 2014) (Learn how and when to remove this message) Reciprocating internal combustion engine Ir...

Si ce bandeau n'est plus pertinent, retirez-le. Cliquez ici pour en savoir plus. Cet article doit être actualisé (mai 2018). Des passages de cet article ne sont plus d’actualité ou annoncent des événements désormais passés. Améliorez-le ou discutez-en. Vous pouvez également préciser les sections à actualiser en utilisant {{section à actualiser}}. Cette liste des établissements pénitentiaires français regroupe les établissements pénitentiaires français gérés par l'adminis...

はやかわ けんいち早川 賢一(Hayakawa Kenichi)基本資料代表國家/地區 日本出生 (1986-04-05) 1986年4月5日(38歲)[1] 日本滋賀縣大津市[1]身高1.77米(5英尺91⁄2英寸)[1]體重79公斤(174英磅)[1]握拍右手[1]主項:男子雙打、混合雙打首戰國際賽2005年退役2017年世界冠軍頭銜 汤姆斯杯:1職業戰績9勝–3負(男單)256勝–151負(男雙)90勝–96負�...

American mobster (1906–1947) Bugsy SiegelSiegel in 1944BornBenjamin Siegel[1](1906-02-28)February 28, 1906New York City, U.S.DiedJune 20, 1947(1947-06-20) (aged 41)Beverly Hills, California, U.S.Cause of deathGunshot woundsResting placeHollywood Forever CemeteryOther namesBen, Benny [2]Spouse Esta Krakower (m. 1929; div. 1946)PartnersWendy Barrie (1942–1943)Virginia Hill (1945–1947)Children3Signature Benj...

Ford France - Ford SAF Création 1916 Dates clés 1929 : réorganisation et renommée Ford SAF1954 : Ford SAF rachetée par Simca1973 : ouverture de l'usine de boîtes de vitesses à Bordeaux12 juin 2002 : immatriculation de la société commerciale actuelle (FMC) Disparition 2000 Fondateurs Henry Ford Personnages clés Maurice Dollfus, dirigeant de Ford SAF de 1930 à 1950 Forme juridique Société par actions simplifiée à associé unique Siège social Nanterre Île de...

La XIe dynastie est une lignée de rois originaires de Thèbes (Ouaset) ayant régné sur l'Égypte de : -2160 à -1994 selon Aidan Mark Dodson (avec Antef Ier), -2125 à -1985 selon Ian Shaw, -2124 à -1980 selon Jaromír Málek (avec Antef Ier), -2119 à -1973 selon Jürgen von Beckerath, -2077 à -1938 selon Detlef Franke. Elle fait partie de la Première Période intermédiaire, jusqu'à la prise de la capitale de la Xe dynastie en -2022, elle est ensuite classée comme la...















