Péndulo físico
|
Read other articles:

Jalan di Azerbaijan adalah jaringan transportasi utama di Azerbaijan. Saat ini jaringan kereta api masih menjalani modernisasi dan tidak mencakup seluruh wilayah negara, terutama daerah pegunungan dan daerah lain dengan topografi yang sulit, sehingga sistem jalan adalah sarana transportasi terpenting di negara ini. Perannya sangat penting baik untuk lalu lintas nasional, dan lalu lintas internasional karena Azerbaijan merupakan suatu negara transit yang penting. Ikhtisar Total panjang jaring...

Jinshi Hanzi tradisional: 進士 Hanzi sederhana: 进士 Alih aksara Mandarin - Hanyu Pinyin: jìnshì - Wade-Giles: chin⁴-shih⁴ Jinshi (Hanzi: 進士; Pinyin: jìnshì) adalah tingkat tertinggi dan terakhir dalam ujian kenegaraan pada masa Kekaisaran Tiongkok.[1][2] Ujian ini biasanya diadakan di ibu kota, di dalam istana, sehinga disebut juga Ujian Ibu kota. Mereka yang berhasil lulus ujian tingkat akhir ini dinamakan jinshi, terkadang diterjemahkan menjadi Sarj...

Pour les articles homonymes, voir Nanjing (homonymie) et Nankin (homonymie). Nankin 南京 ; Nanjing (de haut en bas, de gauche à droite) Vue de Nankin avec le lac Xuanwu au centre et la montagne Pourpre au fond.Le mausolée de Sun Yat-sen.Une sculpture représentant un Pixiu.Le chemin spiritiuel conduisant au tombeau Xiaoling.Le temple Jiming (en).Le stade du Centre sportif olympique de Nankin.La porte Yijiang et les remparts de Nankin (en).La rivière Qinhuai (en) et l...

Violeta Chamorro Nama dalam bahasa asli(es) Violeta Barrios de Chamorro BiografiKelahiran18 Oktober 1929 (94 tahun)Rivas Presiden Nikaragua 25 April 1990 – 10 Januari 1997 ← Daniel Ortega – Arnoldo Alemán → Data pribadiPendidikanOur Lady of the Lake University Blackstone College for Girls KegiatanPekerjaanpolitikus, wartawan PeriodeAbad ke-20 Partai politikUni Oposisi Nasional KeluargaPasangan nikahPedro Joaquín Chamorro Cardenal (1950–1978) AnakCris...

Questa voce o sezione sull'argomento centri abitati della Spagna non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Segui i suggerimenti del progetto di riferimento. Valverde de Leganéscomune Valverde de Leganés – Veduta LocalizzazioneStato Spagna Comunità autonoma Estremadura Provincia Badajoz TerritorioCoordinate38°40′23.88″N 6°58�...

Messier 69M69 difoto dari Hubble Space Telescope; 3.5′ Kredit: NASA/STScI/WikiSkyData pengamatan (J2000 epos)KelasV[1]Rasi bintangSagittariusAsensio rekta 18j 31m 23.10d[2]Deklinasi −32° 20′ 53.1″[2]Jarak29.7 ribu tcMagnitudo tampak (V)+8.31[3]Dimensi tampak (V)9′.8Karakteristik fisikRadius42 tc[4]MetalisitasTemplat:Fe/H dexPerkiraan umur13.06 Miliar tahun[5]Nama lainM69, NGC 6637, GCl 96[3]...

Political term in Imperial Japan Mainland JapanNative name: 内地Passports for passengers between Mainland Japan and Okinawa during 1952–1972.GeographyLocationJapanDemographicsEthnic groupsJapanese peopleAinu peopleRyukyuan people Mainland Japan (内地, naichi, lit. inner lands) is a term used to distinguish Japan's core land area from its outlying territories. It is most commonly used to distinguish the country's four largest islands (Hokkaidō, Honshū, Kyūshū and Shikoku) from smalle...

Newspaper in Oregon, U.S. The OutlookTypeBiweekly newspaperOwner(s)Pamplin Media GroupManaging editorSteve BrownFounded1911LanguageEnglishCityGresham, Oregon, U.S.Circulation9,068 (as of 2022)[1]Websitetheoutlookonline.com The Outlook is a newspaper published in Gresham, Oregon, a suburb of Portland in the U.S. state of Oregon. It was founded in 1911,[2][3] and is currently owned by the Pamplin Media Group. History It was named the Gresham Outlook from 1911 to 1991...

Đảng ủy Công an Trung ươngViệt Nam Đảng kỳ Đảng Cộng sản Việt Nam Thành viên Bí thư Lương Tam Quang Phó Bí thư Trần Quốc Tỏ Ủy viên Thường vụ Nguyễn Phú TrọngPhạm Minh ChínhTô LâmLê Quốc HùngLê Văn TuyếnNguyễn Văn Long Cơ cấu tổ chức Cơ quan chủ quản Ban Chấp hành Trung ương Đảng Cộng sản Việt Nam Chức năng Lãnh đạo mọi mặt công tác trong công an. Cấp hành chính Cấp Trung ương ...

Theater Army of the U.S. Army United States Army CentralShoulder sleeve insigniaActive1918–191932–741982–presentCountry United StatesBranch ArmyTypeArmy Service Component Command/Theater ArmyRoleHeadquartersPart of U.S. Department of the Army U.S. Central CommandGarrison/HQShaw Air Force Base, South CarolinaNickname(s)Patton's OwnMotto(s)Tertia Semper Prima(Latin for Third Always First)Colors White and redWars World War I Occupation of Germany World War II Occ...

Jon ForemanJon Foreman in April 2008Informasi latar belakangNama lahirJonathan Mark ForemanNama lainJonLahir22 Oktober 1976 (umur 47), San Bernardino County, CaliforniaAsalAmerika SerikatPekerjaanPenyanyi, Pengarang laguInstrumenVokal, Gitar, harmonika, piano, trompet, mandolinTahun aktif1996–sekarangLabellowercase people recordsArtis terkaitSwitchfoot, Fiction FamilySitus webjonforeman.com Jonathan Mark Foreman (lahir 22 Oktober 1976) adalah seorang gitaris dan salah satu pendiri grup...

Códigos de marcado empleados por los nazis. Insignia amarilla. Los campos de concentración nazis poseían un sistema de marcaje de prisioneros basado principalmente en triángulos invertidos. Los triángulos estaban hechos de tela y se cosían sobre las chaquetas y camisas de los prisioneros. Estas marcas eran obligatorias y tenían significados concretos que servían para distinguir las razones por las que el prisionero había sido ingresado en el campo.[1] Codificación Orden en el...

Venezuelan footballer (born 1997) In this Spanish name, the first or paternal surname is Quero and the second or maternal family name is Albarracín. Eduin Quero Quero in 2017Personal informationFull name Eduin Estiwer Quero Albarracín[1]Date of birth (1997-04-22) 22 April 1997 (age 27)Place of birth San Cristóbal, Táchira, Venezuela[1]Height 1.72 m (5 ft 8 in)[1]Position(s) Left-backTeam informationCurrent team AngosturaNumber 23Youth ca...

العلاقات الهندية الإيطالية الهند إيطاليا الهند إيطاليا تعديل مصدري - تعديل العلاقات الهندية الإيطالية هي العلاقات الثنائية التي تجمع بين الهند وإيطاليا.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية للدولتين: وجه المقارنة اله�...

American novelist, screenwriter, historian, and literary historian A. B. Guthrie Jr.Born(1901-01-13)January 13, 1901Bedford, Indiana, U.S.DiedApril 26, 1991(1991-04-26) (aged 90)Choteau, Montana, U.S.EducationUniversity of WashingtonUniversity of Montana (BA)OccupationAuthor Alfred Bertram Bud Guthrie Jr. (January 13, 1901 – April 26, 1991) was an American novelist, screenwriter, historian, and literary historian known for writing western stories. His novel The Way West won the 1950 Pu...

Natural satellite orbiting Earth This article is about Earth's natural satellite. For moons in general, see Natural satellite. For other uses, see Moon (disambiguation). MoonNear side of the Moon, lunar north pole at topDesignationsDesignationEarth IAlternative namesLunaSelene (poetic)Cynthia (poetic)AdjectivesLunarSelenian (poetic)Cynthian (poetic)Moonly (poetic)Symbol or Orbital characteristicsEpoch J2000Perigee362600 km(356400–370400 km)Apogee405400 km(404000–406700 ...

Daratan Marie Byrd. Tanah Marie Byrd adalah wilayah di Antarktika Barat yang terletak di sebelah timur paparan es Ross dan Laut Ross serta di sebelah selatan Samudra Pasifik. Nama wilayah ini diberikan oleh Richard E. Byrd pada tahun 1929 untuk mengenang istrinya.[1] Tempat ini sangat terpencil, sehingga sebagian besar wilayah Marie Byrd (di sebelah timur 150°W) belum diklaim oleh negara manapun. Sejauh ini Daratan Marie Byrd merupakan daratan terbesar yang belum diklaim di dunia den...

ウィリアム・ブレイクの著書に書かれたことわざ ことわざ(諺、英語: proverb、ラテン語: proverbium)とは、民間説話の下位概念であり、「人口に膾炙された」言句をいい、鋭い風刺や教訓・知識などを含んだ、世代から世代へと言い伝えられてきた簡潔な言葉のことである。俚諺(りげん)ともいう[1]。「故事・成句」などと関連する。 概要 ことわざは、観�...
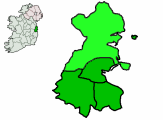
Extinct Middle English dialect of eastern Ireland For the Gaelic Athletic Association club, see Fingallians GAA. FingallianNative toIrelandRegionFingalExtinctMid-19th century[citation needed]Language familyIndo-European GermanicWest GermanicNorth Sea GermanicAnglo-FrisianAnglicFingallianEarly formsProto-Indo-European Proto-Germanic Proto-West Germanic Proto-English West Saxon Old English[1] Middle English Language codesISO 639-3None (mis)Glottologeast2834fing1234 Fingalli...

Verlauf Der Migrationstreck von Zentralamerika bis zur Grenze zwischen Mexiko und den Vereinigten Staaten war ab Oktober 2018 ein Zug von mehreren tausend Migranten – vorwiegend Menschen aus der landlosen, vielfach indigenen Landbevölkerung – aus zentralamerikanischen Ländern wie El Salvador, Guatemala oder Honduras, die sich in Fußmärschen über bis zu 2000 km weit durch Mexiko in Richtung der US-amerikanischen Außengrenze bewegten zwecks Einwanderung in die Vereinigten Staaten...




















