Función zeta local
|
Read other articles:

Indarto Budiarto Kapok Sahli Koarmada IIMasa jabatan27 Juni 2022 – 4 November 2022 PendahuluEko Gajah SenoPenggantiEndra Sulistiyono Informasi pribadiLahir5 November 1964 (umur 59)Kutoarjo, Purworejo, Jawa TengahAlma materAkademi Angkatan Laut (1988)Karier militerPihak IndonesiaDinas/cabang TNI Angkatan LautMasa dinas1988—2022Pangkat Laksamana Pertama TNINRP9182/PSatuanKorps PelautSunting kotak info • L • B Laksamana Pertama TNI (Purn.) Indarto Budiar...

Lokasi Masjid terkait dengan benteng dan istana Ázm Bab al-Jabiyah (Arab: بَابُ الْجَابِيَّةِ, romanized: Bāb al-Jābīyahcode: ar is deprecated ; Gate of the Water Trough) adalah salah satu air dari tujuh gerbang kota kuno yang berada di Damaskus, Suriah. Selama era Romawi, gerbang itu didedikasikan untuk Mars.[1] Bab al-Jabiya adalah pintu masuk utama yang ada di sisi barat kota. Gerbang itu berada di Midhat Pasha Souq (bazar) yang mana merupakan bagian dari...

Untuk kegunaan lain, lihat Pengabdi Setan. Pengabdi SetanPoster filmSutradaraJoko AnwarProduserGope T. SamtaniDitulis olehJoko AnwarBerdasarkanPremis yang disarankan oleh Pengabdi Setanoleh Sisworo Gautama PutraPemeran Tara Basro Bront Palarae Endy Arfian Adhiyat Ayu Laksmi Dimas Aditya Elly D. Luthan Penata musik Aghi Narottama Bemby Gusti Tony Merle SinematograferIcal TanjungPenyuntingArifin CuunkPerusahaanproduksi Rapi Films CJ Entertainment DistributorRLJE FilmsTanggal rilis 28 Sept...

The following is a list of notable films produced in Iceland by Icelanders. Star marked films are films in coproduction with Iceland. Although Arne Mattsson is Swedish, his film is included because it is based on a book by the Icelandic Nobel Prize-winning author Halldór Laxness. 1900–1979 Year Original title English title Director 1915 Breiðafjarðareyjar Breiðafjarðareyjardocumentary 1923* Hadda Padda Hadda Paddaco-production Gunnar Robert Hansen Guðmundur Kamban 1923 Ævintýri Jó...

Major League Baseball season Major League Baseball team season 2007 Boston Red SoxWorld Series ChampionsAmerican League ChampionsAmerican League East ChampionsLeagueAmerican LeagueDivisionEastBallparkFenway ParkCityBoston, MassachusettsRecord96–66 (.593)Divisional place1stOwnersJohn W. Henry (New England Sports Ventures)PresidentLarry LucchinoGeneral managerTheo EpsteinManagerTerry FranconaTelevisionNew England Sports NetworkRadioWRKOWEEIWROL (Spanish)StatsESPN.comBB-reference ←&...

Trisula pada patung Poseidon di Kopenhagen. Trisula atau serampang (Sanskerta: trishul; bahasa Inggris: trident) adalah tombak bermata tiga yang secara harfiah berarti tiga tombak. Trisula juga digunakan oleh retarii, gladiator dengan penampilan seperti nelayan (membawa jaring). Trisula saat ini sering diasosiasikan dengan setan oleh mitologi Kristen. Ini kemungkinan karena penggunaannya dalam agama pagan. Trisula adalah senjata Siwa, salah satu dari Trimurti yang sering disembah pada masa ke...

Google Developer DayLogo Google Developer DayFrekuensiSetiap tahunPenyelenggaraGoogleSitus webhttp://www.google.com/events/developerday Google Developer Day 2008 di Taiwan Google Developer Day adalah kegiatan pengembang web selama satu hari yang diadakan di seluruh dunia setiap tahunnya oleh Google. Kegiatan ini meliputi seminar dan bedah kode yang bertujuan membangun aplikasi web, bergerak, dan perusahaan bersama Google dan teknologi web terbuka seperti Android, HTML5, Chrome, App Engine, Go...

Bupati Pulau TaliabuPetahanaAliong Mussejak 26 Februari 2021Masa jabatan5 tahun dan dapat dipilih kembali untuk satu kali masa jabatanDibentuk22 April 2013; 10 tahun lalu (2013-04-22)Pejabat pertamaArman Sangaji (Penjabat)Aliong Mus (definitif)Situs webSitus web resmi Berikut adalah daftar Bupati Taliabu secara definitif sejak tahun 2016 pasca pemekaran Kabupaten Pulau Taliabu dari Kabupaten Kepulauan Sula. Nomor urut Bupati Potret Partai Awal Akhir Masa jabatan Periode Wakil Ref. 1...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Battle of Leskovac – news · newspapers · books · scholar · JSTOR (May 2014) (Learn how and when to remove this message) 15th-century battle Battle of LeskovacSerbian Despotate 1451, part of the Ottoman wars in EuropeDateSeptember 24, 1454Locationnear Leskovac, ...

Indian television channel This article is about the television channel available in India. For the Hindi language television channel available in the Middle East and North Africa, see Cartoon Network Hindi. Television channel Cartoon NetworkCountryIndiaBroadcast area India Bangladesh Bhutan[1] Nepal Sri Lanka HeadquartersMumbai, Maharashtra, IndiaProgrammingLanguage(s) Hindi Tamil Telugu Kannada Malayalam Picture format16:9, 4:3 or letterboxed (576i SDTV)(1080i for the HDTV feed)Owner...

American and Canadian fur trader Robert StuartBorn(1785-02-19)February 19, 1785Strathyre, Perthshire, ScotlandDiedOctober 28, 1848(1848-10-28) (aged 63)Detroit, Michigan, U.S.Occupation(s)Fur trader, explorerSpouseEmma Elizabeth Sullivan Robert Stuart (February 19, 1785 – October 28, 1848) was a Scottish-born, Canadian and American fur trader, best known as a member of the first European-American party to cross South Pass during an overland expedition from Fort Astoria to Saint Louis i...

此條目可能包含不适用或被曲解的引用资料,部分内容的准确性无法被证實。 (2023年1月5日)请协助校核其中的错误以改善这篇条目。详情请参见条目的讨论页。 各国相关 主題列表 索引 国内生产总值 石油储量 国防预算 武装部队(军事) 官方语言 人口統計 人口密度 生育率 出生率 死亡率 自杀率 谋杀率 失业率 储蓄率 识字率 出口额 进口额 煤产量 发电量 监禁率 死刑 国债 ...
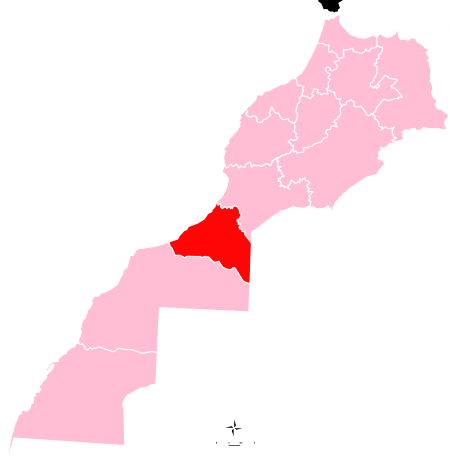
Place in Guelmim-Oued Noun, MoroccoAssa آساAssaLocation in MoroccoShow map of MoroccoAssaAssa (Africa)Show map of AfricaCoordinates: 28°36′31″N 9°25′37″W / 28.60861°N 9.42694°W / 28.60861; -9.42694Country MoroccoRegionGuelmim-Oued NounPopulation (2012) • Total18,367[1]Time zoneUTC+0 (WET) • Summer (DST)UTC+1 (WEST) Assa (Arabic: آسا) is a small town in southern Morocco, in the Assa-Zag province of the Guelmim-...

American attorney Eric GonzalezGonzalez in 2023District Attorney of Kings CountyIncumbentAssumed office October 9, 2016Acting: October 9, 2016 – January 21, 2018Preceded byKenneth P. Thompson Personal detailsBorn (1969-01-24) January 24, 1969 (age 55)New York City, New York, U.S.Political partyDemocraticEducationCornell University (BA)University of Michigan (JD) Eric Gonzalez (born January 24, 1969)[1] is an American attorney who is currently serving as the district attorne...

Scottish journalist and rationalist (1856–1933) John Mackinnon RobertsonBorn14 November 1856Brodick, Isle of Arran, ScotlandDied5 January 1933 (aged 76)London, EnglandOccupation(s)Journalist, politician, rationalist, writer John Mackinnon Robertson PC (14 November 1856[1] – 5 January 1933[2]) was a prolific Scottish journalist, advocate of rationalism and secularism, and Liberal Member of Parliament for Tyneside from 1906 to 1918. Robertson was best known as an advocate of...

Political party in Australia For the Australian party (1989–1991), Joh Bjelke-Petersen, see Australian Conservative Party. For the Australian party (1984–1998), see Conservative Party of Australia. Australian Conservatives LeaderCory Bernardi[a]FounderCory BernardiFounded7 February 2017; 7 years ago (7 February 2017)[b]Dissolved25 June 2019Split fromLiberal PartyHeadquartersKing William Street, Kent Town, South Australia 5067Membership (2017) 22,000[c...

2005 meeting of the G8 countries in Auchterarder, Scotland 31st G8 summitOfficial logoHost countryUnited Kingdom (Scotland)Date6–8 July 2005Follows30th G8 summitPrecedes32nd G8 summit The 31st G8 summit was held on 6–8 July 2005 at the Gleneagles Hotel in Auchterarder, Scotland and hosted by Prime Minister Tony Blair. The locations of previous G8 summits to have been hosted by the UK include: London (1977, 1984, 1991); and Birmingham (1998). It is the first G8 summit to be held in Scotlan...

Pour les articles homonymes, voir Shining. Shining :Les Couloirs de la peur Photo du Stanley Hotel, qui servit à la réalisation de la mini-série. Données clés Titre original The Shining Autres titresfrancophones Shining : Les Couloirs du tempsShining : Les Couloirs de la mort Genre mini-série horrifique Création Stephen King Production Mark CarlinerElliot FriedgenLaura GibsonStephen King Acteurs principaux Steven WeberRebecca De MornayCourtland Mead Musique Nicholas Pik...

Australian federal election 1929 Australian federal election ← 1928 12 October 1929 (1929-10-12) 1931 → ← outgoing memberselected members →All 76[b] seats in the Australian House of Representatives38 seats were needed for a majorityRegistered3,539,120 2.74%Turnout2,957,549 (94.85%)[a](1.21 pp) First party Second party Leader James Scullin Stanley Bruce Party Labor Nationalist/Country coalition Leader ...

Rais Abin Anggota Majelis Permusyawaratan RakyatMasa jabatan1 Oktober 1999 – 1 Oktober 2004Duta Besar Indonesia untuk Singapura Masa jabatan1984 – 25 Agustus 1988PresidenSuhartoPendahuluSudjatmikoPenggantiTuk SetyohadiDuta Besar Indonesia untuk Malaysia Masa jabatan6 Agustus 1981 – 22 September 1984PresidenSuhartoPendahuluMakmun MurodPenggantiHimawan Soetanto Informasi pribadiLahir(1926-08-15)15 Agustus 1926Koto Gadang, Agam, Hindia BelandaMeninggal25 Maret 20...












